Урок-семинар на тему «Прямые и плоскости в пространстве»

Министерство образования Саратовской области

Государственное автономное профессиональное образовательное учреждение

Саратовской области «Новоузенский агротехнологический техникум»

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

Проведения урока-семинара по математике на тему:

«Прямые и плоскости в пространстве»

Выполнила: Устинова Н.Н.,

Преподаватель математики

г. Новоузенск

Цель урока-семинара:

1. Углубить, обобщить систематизировать и закрепить полученные знания по стереометрии.

2. Развивать у учащихся абстрактное пространственное мышление.

3. Воспитывать культуру речи, аккуратность при выполнении чертежей.

План урока:

1. Обзорная лекция по теме: «Прямые и плоскости в пространстве». 20 мин.

2. Решение задач по стереометрии. 135 мин.

3. Задание на дом. 3мин.

4. Подведение итогов урока. 2мин.

Оборудование урока: портреты великих математиков, мультимедиапроектор, интерактивная доска, плакат игры «Лабиринт», карточки, рефераты.

Во время обзорной лекции желательно назвать имена великих математиков от Евклида до Лобачевского, в трудах которых изучались вопросы данной темы, показать их портреты. Лекцию можно построить по следующему плану:

1. Аксиомы стереометрии и их следствия.

2. Взаимное расположение прямых в пространстве.

3. Взаимное расположение прямой и плоскости.

4. Взаимное расположение плоскостей.

5. Изображение пространственных фигур на плоскости.

6. Угол и расстояние между скрещивающимися прямыми.

Лекцию желательно сопровождать рисунками, в которых наглядно представлены случаи взаимного расположения в пространстве двух прямых, прямой и плоскости, двух плоскостей.

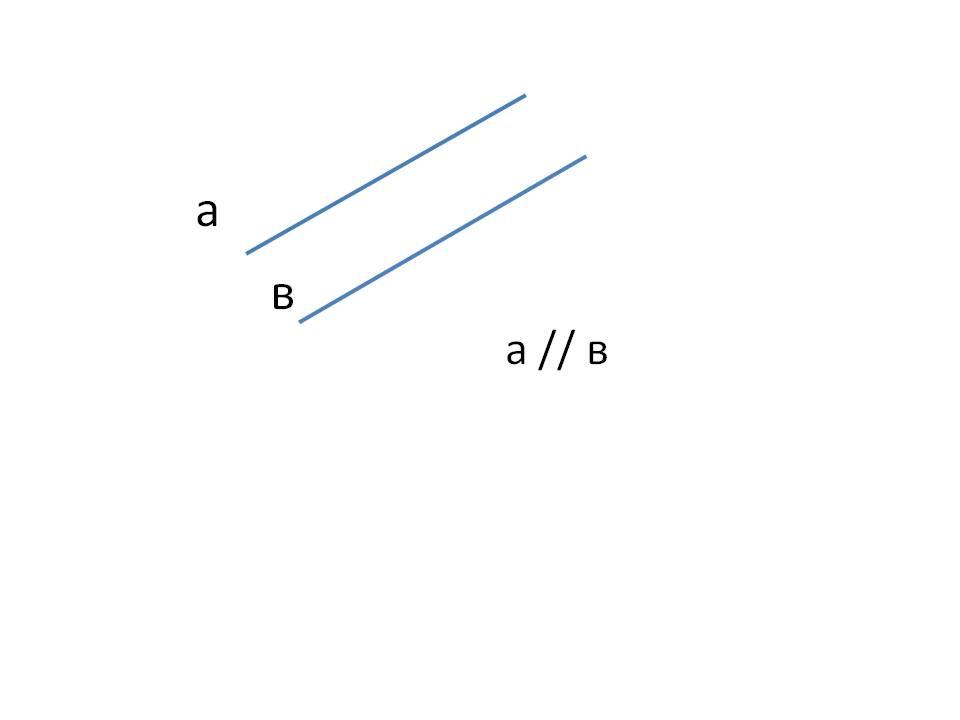
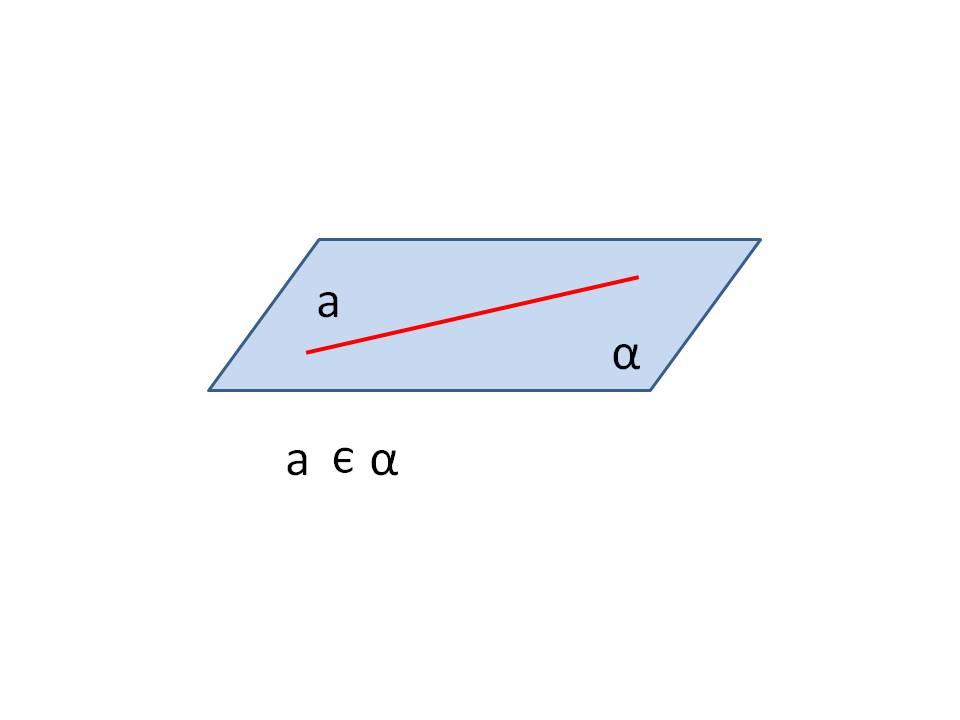
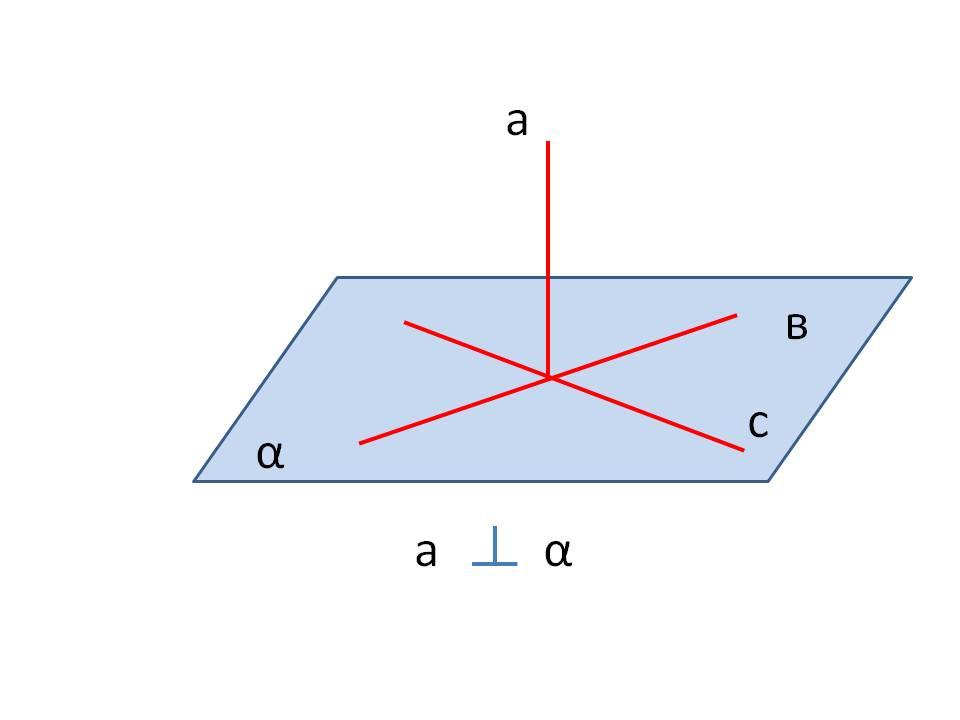
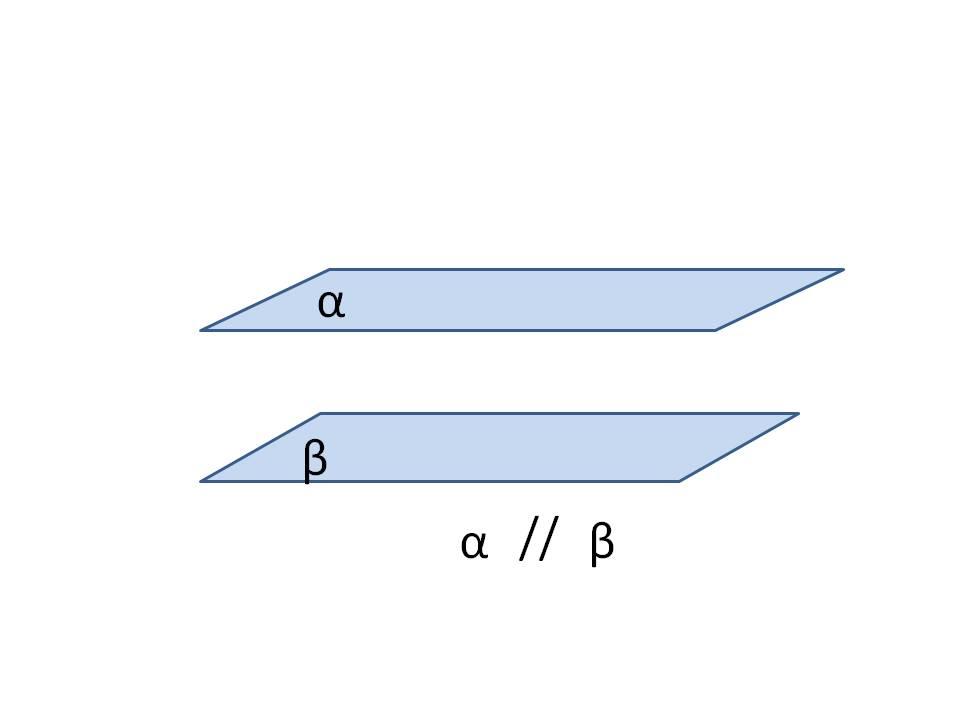
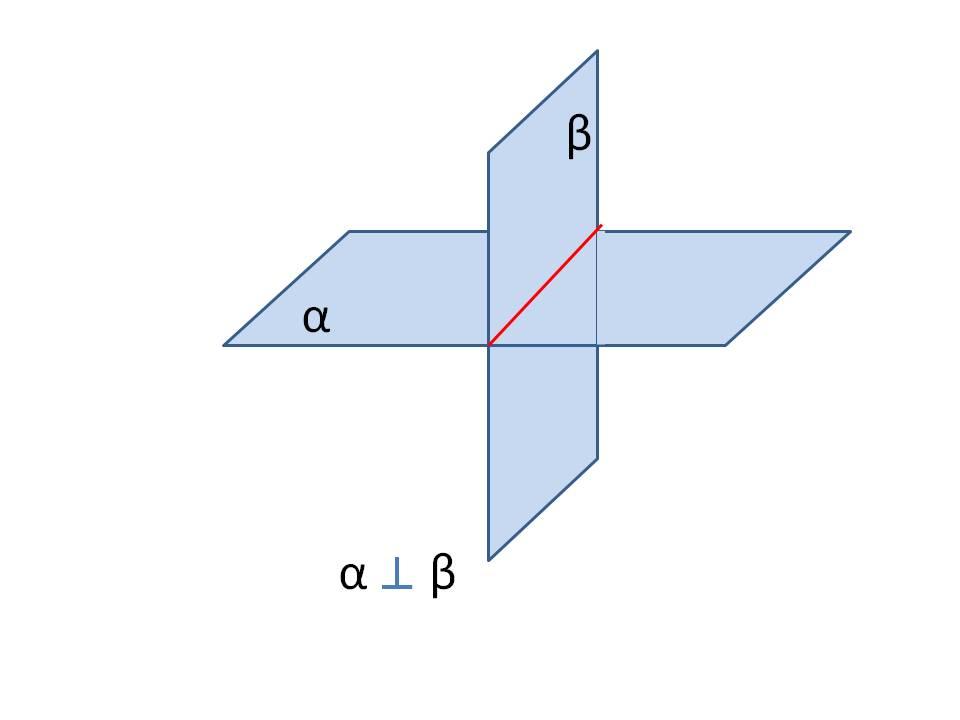
Логическим дополнением к лекции является беседа учителя с классом по ряду предложенных задач. При этом необходимо подчеркнуть студентам, что в стереометрических задачах большое значение при решении имеет удачно выполненный чертёж. Изображение пространственных фигур всегда возможно лишь с искажениями, поэтому чертёж нужно правильно понимать. Этапом решения стереометрических задач является логическое обоснование любого факта, сколь бы очевиден он ни был из чертежа.

Задачи для урока-семинара проектируются на интерактивную доску и расширяются устно.

Задача № 1. Прямые a и b параллельны, а прямая с пересекает a и b. Доказать что прямые a, b, c лежат в одной плоскости.

Задача № 2. Объясните в чем состоит сходство и различие скрещивающихся и параллельных прямых в пространстве.

Задача № 3. Прямые a и b параллельны. Докажите, что если α пересекает прямую а, то она пересекает и прямую b.

Задача № 4. Докажите, что через произвольную точку Р, лежащую на прямой p, можно провести плоскость α,перпендикулярную прямую p.

Задача № 5. Из вершины прямого угла С треугольника ABC восстановлен к плоскости этого треугольника перпендикуляр СМ=28 см.

Найти расстояние от точки М до гипотенузы треугольника ABC, если его катеты равны 16 см и 12 см.

Чтобы увидеть, насколько хорошо усвоен теоретический материал и как на практике применяют полученные знания, а так же с целью активизации студентов на заключительном этапе урока-семинара можно предложить студентам провести игру «Лабиринт». Группа разбивается на 3 команды, выбирается капитан каждой команды. На предыдущем уроке преподаватель предварительно ознакомил группу с условиями игры, предупредил о том, какие темы будут вынесены для закрепления.

Для проведения игры готовится заранее оборудование: секундомер, схемы «лабиринта», игральный кубик, призы. К каждой команде прикрепляется эксперт для контроля за правильностью ответов и объяснения возникающих вопросов. Игра вызывает дух соревнования, будит эмоции студентов, заставляет удивиться, а очень важно, ведь ещё Аристотель когда-то мудро заметил, что «мышление начинается с удивления».

Каждой команде выдаётся по 3 конверта с текстами задач по трём разделам темы, карточная схема «Лабиринта» и игральный кубик. Капитаны команд поочерёдно кидают кубик, выпавшее число означает номер задания из первого раздела. Эксперт следит за правильным выполнением игры. Если задача решена, команда, не подбрасывая кубик, переходит по «лабиринту» к теме №2 на этот номер задачи, с которым соединена первая ими решённая задача. Если задача не решена, то эксперт разъясняет её, а команда остаётся на той же теме и вторично подбрасывает кубик, чтобы узнать номер новой задачи, которую надо решить. Команда может подбросить кубик не более 2 раз, если обе попытки неудачны, то команда выбывает из игры.

Команда, которая первой закончила все задачи, выпавшие ей в «лабиринте» становится победительницей.

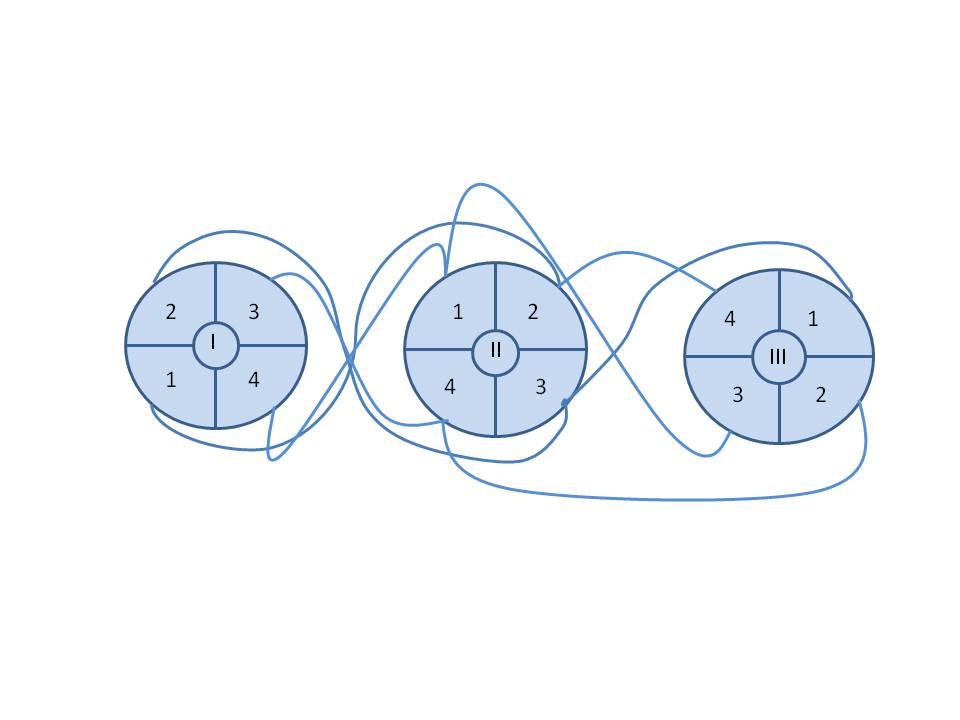
Задания, предлагавшиеся для игры.

1. Параллельные прямые

Задание № 1. Концы данного отрезка длиной 50 см отстоят от плоскости на 30 и 44 см. найти проекцию этого отрезка на плоскость.

Задание № 2. Отрезок длиной 15 см пересекает плоскость, концы его отстоят от плоскости на 3 и 6 см. найти проекцию этого отрезка на плоскость.

Задание № 3. Отрезок пересекает плоскость, концы его отстоят от плоскости на 3 и 12 см. найти расстояние середины этого отрезка от плоскости.

Задание 3 4. Отрезок пересекает плоскость, концы его отстоят от плоскости на 5 и 15 см. Найти расстояние середины этого отрезка от плоскости.

1. Теорема о трех перпендикулярах

Задание № 1. Из вершины прямого угла прямоугольного треугольника с катетами 15 и 20 см проведен перпендикуляр длиной 16 см к плоскости треугольника. Найти расстояние от концов перпендикуляра до гипотенузы.

Задание № 2. Стороны треугольника равны 51,3 и 27 см. из вершины меньшего угла треугольника проведен к его плоскости перпендикуляр длиной 10 см. найти расстояние от концов перпендикуляра до противолежащей стороны треугольника.

Задание № 3. в треугольнике, стороны которого равны 10, 17 и 21 см, из вершины большего угла проведен перпендикуляр к его плоскости, равный 15 см. вычислить расстояние от конца этого перпендикуляра, лежащего вне плоскости треугольника, до большей стороны треугольника.

Задание № 4. Диагонали ромба равны 60 и 80 см: в точке пересечения диагоналей к плоскости ромба проведен перпендикуляр длиной 45 см. найти расстояние от этой точки до стороны ромба.

1. Изображение пространственных фигур на плоскости

Задание № 1. Изобразить параллелепипед.

Задание № 2. Изобразить цилиндр.

Задание № 3. Изобразить пирамиду.

Задание № 4. Изобразить куб.

Домашнее задание на повторение предлагается в виде подготовки рефератов. Учебник не является при этом единственным источником знаний. Студенты работают самостоятельно, используя дополнительную литературу, справочники по математике, решают задачи, предложенные преподавателем.

Темы для рефератов:

«Геометрия и семь чудес света», «Изображение пространственных фигур на плоскости», «Методы построения плоских сечений», «Координаты и векторы в пространстве». Сильным студентам можно предложить задачи повышенной трудности для самостоятельного решения. При правильной организации работы студенты на уроке- семинаре при подведении итогов каждый получает оценку комментарием преподавателя.

Заключение

Предлагаемая форма проведения урока – семинара относится к нестандартным видам работы студентов на уроке (опрос, решение задач и т.д.). Она привлекает всех ребят к участию в обсуждаемых вопросах, активирует их внимание, при этом используется сочетание индивидуального подхода к студентам с разными способностями и групповая работа. Данная форма обучения применяется нечасто, требует особых организационных усилий, на зато дает заметный эффект не только в обучении, но и в воспитании студентов.

Список используемой литературы

1. А.Д. Александров, А.П. Вернер, В.И. Рыжик. Начала стереометрии, пособие для преподавателя.

2. Н.В. Богомолов. Практические занятия по математике.

3. Журнал «Математика в школе»