Тема урока: Тригонометрические функции их свойства и графики.
Цели урока:
Обучающая: закрепить основные свойства тригонометрических функций, умение строить их графики и показать их практическое применение.
Развивающая: способствовать формированию ключевых компетентностей, развитие графических навыков, умение применять свои знания на практике.
Воспитательная: воспитание устойчивого интереса к изучению математики, самоконтроля, интереса к решению задач, математической культуры.
Оборудование : проектор, компьютер, интерактивная доска. На партах учащихся таблицы со списком уравнений; листочки для записи ответов, оценочные листы и критерии оценок.
Я всех вас, дорогие друзья, рада видеть сегодня на уроке! И поэтому я спешу сказать вам: «Здравствуйте!» Чтоб пожелать здоровья доброго, я спешу сказать вам «Благости!» Чтоб пожелать вам счастья нового, я спешу сказать вам: «Радости! Удач, успехов и везенья!» Чтоб пожелать вам в этом классе Прекраснейшего настроения!!!..
Дорогие друзья! улыбнитесь друг другу, подарите улыбки мне и нашим гостям. Давайте настроимся на работу- откроим ладошки новым знаниям и произнесём нашу волшебную фразу: «Я хочу много знать!» . Посмотрите на картинки и напишите номер той, которая соответствует вашему настроению на начало урока.
На экране слайд №3
Откройте тетради и запишите дату и тему урока.
Ассистенты сообщают о выполнении классом домашнего задания.
1.Актуализация знаний.
Работа устно. Разминка. Учитель называет имя ученика, бросает ему мяч и задаёт ему вопрос. Тот в свою очередь называет имя следующего ученика и задаёт ему свой вопрос по теме урока. И т.д.
2.Закрепление. Следующую работу проведём в виде «своя игра»
Класс разбивается на 3 команды. По жеребьёвке начинаем игру.
I Раунд.
Периодичность, чётность
100 очков. Какие из заданных функций не являются периодическими?
1)y = 1/3cos (2x – π/5) ; 2) y = sin 0,3(x – π/4) - 2 ;
3) y = ctg 3x ; 4) y = 2(x -1)².
Ответ: 4.
Дополнительный вопрос для каждой команды: Указать наименьший период, остальных функций.
Ответ: а)π/2; б)10π/3; в)π/3
200 очков. Какие из данных функций являются чётными?
1) y = 1/3cos5х; 2) y = tg(x + π/8)
3) y = IxI; 4) y = 2(x -1)²
Ответ: 1,3.
300 очков. Как по графику определить чётную и нечётную функцию?
Ответ: График чётной функции симметричен относительно оси OY;
нечётной – относительно начала системы координат.
400 очков: Перевести радианы в градусы:
а) 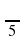 ; б)
; б) 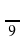 ;
;
в) 5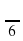 ; г) 7π.
; г) 7π.
Ответ: а) 360 ; б)200; в)1500 ; г)25200.
500 очков: Сформулируйте правило построения графика функции y = kf(x).
Ответ: Для построения графика функции y = kf(x) надо:
если IkI 1, то растянуть график функции y = f(x) в k раз вдоль оси ординат,
если IkI y = f(x) в 1/k раз вдоль оси ординат.
А знаешь ли ты?
![]()
 100 очков: Выберите уравнение, которое имеет решение, показанное на единичной окружности:
100 очков: Выберите уравнение, которое имеет решение, показанное на единичной окружности:
tg x = 1;
sin x = 0;
сos x = 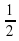 ;
;
sin x = 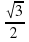 .
.
200 очков:
Какая ошибка допущена в решении уравнения?
Cos( 2x+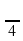 ) =
) =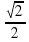
2x + 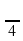 =
=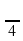 + 2πn,n
+ 2πn,n  Z или 2х = -
Z или 2х = - 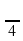 + 2πm,m
+ 2πm,m  Z;
Z;
2х = 2πn, n  Z, 2x = -
Z, 2x = -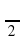 + 2πm,m € Z;
+ 2πm,m € Z;
Х= 4πn, n  Z, х = -π + 4πm, m € Z.
Z, х = -π + 4πm, m € Z.
Ответ: х = πn,n  Z, x = -
Z, x = - 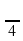 + πn, n € Z.
+ πn, n € Z.
Какой корень уравнения
cos 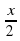 = 1 принадлежит отрезку [ -π; π]?Решить графически с полным объяснением построения
= 1 принадлежит отрезку [ -π; π]?Решить графически с полным объяснением построения
Ответ: 0
Используя график, укажите все точки,
удовлетворяющие неравенству: sin x 0,5.
Найдите значения х, при которых график функции y = 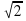 cosx - 1
cosx - 1
лежит выше оси х.
Ответ: (- 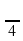 + 2πn;
+ 2πn;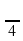 + 2πn), n
+ 2πn), n  Z.
Z.
Как, не решая уравнения ctg2 x = 1 - 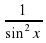 ,
,
определить, какая серия является решением?
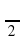 + πn, n
+ πn, n  Z, 3) π + 2πn , n
Z, 3) π + 2πn , n  Z,
Z,
 n, n
n, n  Z, 4)
Z, 4) 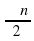 , n
, n  Z.
Z.
Ответ: 1
Найдите все х, обращающие в нуль произведение
функций y = cosx -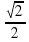 и y = sin 4x .
и y = sin 4x .
Ответ: 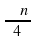 , n
, n  Z.
Z.
Решите уравнение sin 2x – 3 cos x = 0
Ответ: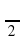 +πn, n
+πn, n  Z.
Z.
Физминутка.
Найдите наименьший положительный
корень уравнения ItgxI = 1 .
Ответ: 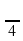 .
.
При каких значениях х значения функции
y = tg(x – 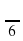 ) равно 0?
) равно 0?
Ответ: 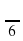 +πn, n
+πn, n  Z.
Z.
При каких значениях а уравнение Cos 5x = a не имеет решений?
Ответ: IaI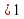
Укажите, используя график, все точки, удовлетворяющие неравенству:
ctg x 1.
Ответ: πn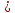 x
x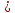
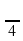 + πn, n
+ πn, n  Z.
Z.
Решите уравнение sin x - 1/2 = b, если одно из его решений 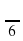 .
.
Ответ: 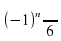 + πn, n € Z.
+ πn, n € Z.
Решите уравнение cos x = cos 3x.
Ответ: 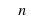 , n
, n Z
Z
Решить уравнение: = 0
Ответ: -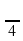 +2
+2 n
n  Z.
Z.
Супер игра
Решить уравнение: 1 + tg2 = x2 +  )2
)2
Ответ: .
.
На столах лежат листочки с заданиями. Уровень выбираете сами.
На «300 баллов»
1.Построить график функции y = 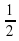 sinx.
sinx.
2.Решить с помощью графика уравнение -cosx = 1.
3.Решить с помощью графика неравенство: tgx 1.
1.
На «400 баллов»
1.Построить график функции y = -sin(х -  )
)
2.Решить с помощью графика уравнение -cosx = 3x – 1.
3.Решить с помощью графика неравенство ctgx 1
1
На «500 баллов»
1.Построить график функции y = 2sin 2 (x - 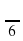 ) +1
) +1
2.Решить с помощью графика уравнение cosx = IxI + 1.
3.Решить с помощью графика неравенство: ctg(x - 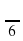 )
) 0
0
Опишите глаголами, что мы делали сегодня на уроке.
Опишите прилагательными, какими вы были сегодня на уроке.
Какие чувства и мысли у вас появились после работы на уроке?
Достиг ли целей урок?
Выберите смайлик соответствующий вашему настроению.
Ребята, нам остался последний этап оценить свою работу.
Домашнее задание:
Повторить && 16- 20
№ 20.4(в,г)
20.5(в,г)
20.21(в,г)
20.26(б)
20.28.(в,г)








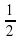
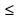
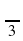 )
)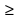
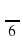 ) +1
) +1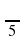 ; б)
; б)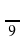
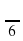 ; г) 7
; г) 7 100 очков: Выберите уравнение, которое имеет решение, показанное на единичной окружности:
100 очков: Выберите уравнение, которое имеет решение, показанное на единичной окружности: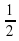 ;
; 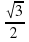
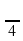 ) =
) =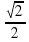

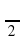 + 2
+ 2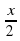 = 1 принадлежит отрезку [ -
= 1 принадлежит отрезку [ -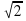
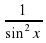 ,
,
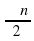 ,
, 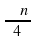 ,
, 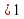
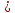
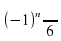 +
+ 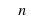 ,
,









 1, то растянуть график функции y = f(x) в k раз вдоль оси ординат, если IkI , то сжать график функции y = f(x) в 1 /k раз вдоль оси ординат" width="640"
1, то растянуть график функции y = f(x) в k раз вдоль оси ординат, если IkI , то сжать график функции y = f(x) в 1 /k раз вдоль оси ординат" width="640"





 0,5." width="640"
0,5." width="640"
![Какой корень уравнения cos = 1 принадлежит отрезку [ - π ; π ] ? х = 0](https://fhd.multiurok.ru/f/7/0/f70eb2fdee93ec1c93a1aa8739e08245ee022973/img_no-name_0_17.jpg)




 1" width="640"
1" width="640"


















