Государственное казенное общеобразовательное учреждение «Средняя общеобразовательная школа № 4» при исправительном учреждении
Урок
«Иррациональные уравнения »
11 класс
Из опыта работы учителя математики
Государственное казенное общеобразовательное учреждение «Средняя общеобразовательная школа № 4» при исправительном учреждении
Овсянникова Евгения Михайловича
(Дата проведения 18.09.2019 год)
Государственное казенное общеобразовательное учреждение «Средняя общеобразовательная школа № 4» при исправительном учреждении
Предмет: математика
Цели урока:
познакомить учащихся с решением некоторых типов иррациональных уравнений;
способствовать развитию навыков решения иррациональных уравнений;
прививать навыки самооценки
формирование компетентностей в сфере самостоятельной познавательной деятельности
Тип урока: комбинированный
Оборудование: карточки с тестом
Ход урока:
I. Организационный момент.
Здравствуйте, ребята. Сегодня мы с вами продолжим изучение темы «Иррациональные уравнения», познакомимся с новыми методами решения уравнений и пройдем небольшой тест на проверку знаний. Но для начала вспомним прошлый материал.
II. Устная работа
Какие уравнения являются иррациональными: (Слайд №3).
а) 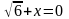 ; б)
; б) 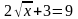 ; в)
; в) 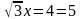 ;
;
г)  ; д)
; д) 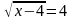 ?
?
Решите уравнение:
а) 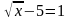 ; б)
; б) 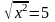 ; в)
; в) 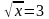 ; г)
; г) 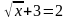 ; д)
; д) 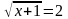 .
.
Найдите область определения функции: (Слайд №5).
а) 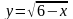 ; б)
; б) 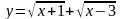 ; в)
; в) 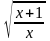 .
.
III. Решение иррациональных уравнений.
Методические примечания:
1. При решении иррациональных уравнений проверка не делается, если используются следующие равносильные преобразования:
А) уравнение вида 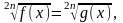 где n
где n 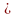 N,
N,
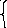
равносильно системе f(x)=g(x),
f(x)=0.
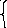
Б) уравнение вида 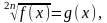 где n
где n 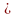 N,
N,
равносильно системе f(x)=g2n(x),
g (x)≥0.
2. Кроме стандартного приема возведения в квадрат (n-ую степень) обеих частей уравнения, при решении иррациональных уравнений иногда очень удобен прием замены переменной, который значительно сокращает время решения.
Пример1 (решение у доски)
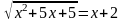
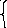
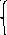
Решение:
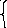 х2+5х+5=(х+2)2 ,
х2+5х+5=(х+2)2 ,  х2+5х+5= х2+4х+4,
х2+5х+5= х2+4х+4,  х = -1,
х = -1,
х+2≥0 , х≥-2, х ≥ -2.
Ответ: х=-1.
Пример2 (самостоятельно)

Решение:
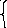
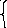
2х-3=х-2 ,  х=1,
х=1,
2х-3≥0 , х≥1,5.
Ответ: решений нет.
Пример3 (решение у доски)

Решение:
Добавим к обеим частям уравнения по 5, получим 
Пусть  , где t ≥0, t2=х2-3х+5.
, где t ≥0, t2=х2-3х+5.
Получим новое уравнение: t2 + t -12=0.
Корни уравнения: t1=3; t2=-4 – не подходит, так как t ≥0.
Вернемся к замене: 
х2-3х+5=9,
х2-3х-4=0,
х1=4; х2=-1.
Проверка подстановкой показывает, что оба корня подходят.
Ответ: -1; 4.
IV. Тестирование (раздается каждому ученику с таблицей ответов, которую они заполняют и сдают учителю).
| Вариант 1
Часть А (оценка 3)
1.  а) а)  ; б) -5; в) 5; г) 25. ; б) -5; в) 5; г) 25. 2.  а) 2; б) 4; в) 8; г) 9. а) 2; б) 4; в) 8; г) 9. 3.  а) 6; б) ± а) 6; б) ± ; в) 36; г) -6. ; в) 36; г) -6. 4.  а) ±4; б) ±2; в) 2; г) -2. а) ±4; б) ±2; в) 2; г) -2. 5.  а) 18; б) ±18; в) -18; г) 6. а) 18; б) ±18; в) -18; г) 6.
Часть В (оценка 4)
1.  а) 8; б) 3; 8; в) 3; г) -3; -8. а) 8; б) 3; 8; в) 3; г) -3; -8. 2.  а) 0; б) 1; в) 0; 1; г) -1. а) 0; б) 1; в) 0; 1; г) -1. 3.  а) -7; б) ±7; в) а) -7; б) ±7; в)  ; г) 7. ; г) 7. 4.  а) -2; 1; б) 2; в) 2; -1; г) -1. а) -2; 1; б) 2; в) 2; -1; г) -1. 5.  а) -10; 3; б) 3; в) -10; г) 10; -3. а) -10; 3; б) 3; в) -10; г) 10; -3.
Часть С (оценка 5)
1.  а) -7; б) 2; в) 7; -2; г) -7; 2; а) -7; б) 2; в) 7; -2; г) -7; 2; 2.  а) нет решений; б) -4; в) -3; г) 1; а) нет решений; б) -4; в) -3; г) 1; 3.  а) -2; 1; б) 1; в) -2; г) -1; 2; а) -2; 1; б) 1; в) -2; г) -1; 2; 4.  а) ; б) ; а) ; б) ; в) ; г) 
|
| Вариант 2
Часть А (оценка 3)
1.  а) а)  ; б) 6; в) -6; г) 36. ; б) 6; в) -6; г) 36. 2.  а) 1; б) 7; в) 5; г) 9. а) 1; б) 7; в) 5; г) 9. 3.  а) 49; б) а) 49; б)  ; в) 7; г) -7. ; в) 7; г) -7. 4.  а) ±5; б) ± а) ±5; б) ± ; в) 8; г) - ; в) 8; г) - . . 5.  а) 36; б) ±6; в) ±20; г) 6. а) 36; б) ±6; в) ±20; г) 6.
Часть В (оценка 4)
1.  а) 1; 5; б) 1; в) 5; г) -1; -5. а) 1; 5; б) 1; в) 5; г) -1; -5. 2.  а) 0; 2; б) 0; в) 2; г) -2. а) 0; 2; б) 0; в) 2; г) -2. 3.  а) -4; б) ±4; в)4; г) 8. а) -4; б) ±4; в)4; г) 8. 4.  а) 0; б) 0; -1; в) -1; г) 0; 1. а) 0; б) 0; -1; в) -1; г) 0; 1. 5.  а) 0; -0,4; б) 0; -2,5; в) 2,5; 0; г) 0,4; 0. а) 0; -0,4; б) 0; -2,5; в) 2,5; 0; г) 0,4; 0.
Часть С (оценка 5)
1. а) 24; б) 8; в) а) 24; б) 8; в) ; г) -24; ; г) -24; 2. а) 3; б) нет решений; в) -1,5; г) -4; 3.  а) 46; б) -1; 46; в) -1; г) 1; 46; а) 46; б) -1; 46; в) -1; г) 1; 46; 4.  а) ; б) ; а) ; б) ; в) ; г)
|
| Ф.И. ученика |
|
| Часть______ | Ответы |
| 1. |
|
| 2. |
|
| 3. |
|
| 4. |
|
V . Итоги урока.
Закончить предложения:
Я могу…
Я оцениваю свои знания на…, потому что…
АСПЕКТНЫЙ АНАЛИЗ УРОКА
| Класс 12 Учитель Овснников Е.М. Предмет алгебра и начала анализа Количество учащихся 24 УМК: программы основного общего образования: Математики 5-11 классы, А.Н. Колмогоров. Рекомендовано департаментом образовательных программ и стандартов общего образования МО РФ 2002 г. Учебник: Алгебра и начала анализа 10-11 классы, А.Н. Колмогоров, «Просвещение» Москва. 2013 год Тип урока: комбинированный. Тема: «Иррациональные уравнения » Цели: познакомить учащихся с решением некоторых типов иррациональных уравнений; способствовать развитию навыков решения иррациональных уравнений; прививать навыки самооценки формирование компетентностей в сфере самостоятельной познавательной деятельности
|
| Этапы урока | Деятельность учителя | Деятельность ученика | Универсальные учебные действия |
| Орг. момент | Приветствие учителя | Приветствие учителя Подготовка рабочих мест | Личностные: -готовность к обучению |
| Постановка темы и целей урока
| Формулировка цели урока |
| Регулятивные: -саморегуляция; -способность принять уч.задачу Коммуникативные: -умение выражать свои мысли |
| Актуализация знаний УДД | Повторение пройденного материала | Формы обучения - фронтальная; Объект восприятия - речь учителя Развитие познават.Д. - словесно-логическая память; - абстрактное мышление -логическая память | Регулятивные: -саморегуляция; - самооценка (формирование осознанного построения речевого высказывания) Коммуникативные: -умение с достаточной полнотой и точностью выражать свои мысли Познавательные: -формирование умения структурировать знания |
| Первичное восприятие и усвоение нового теор. уч. материала | Учебный материал соответствует возрастным особенностям Методы: Словесные (объяснение, рассказ, беседа) Наглядные – работа с компьтером, учебником | Формы обучения Групповая Объект восприятия -речь учителя, -наглядность Развитие познават.Д. - наглядно-образная память - словесно-логическая память; - абстрактное мышление -логическая память | Регулятивные: -саморегуляция; - самооценка -коррекция Коммуникативные: -умение аргументировать свое высказывание, -формирование умения взаимопомощи по ходу работы с компьютером Познавательные: -формирование умения структурировать знания Обратная связь: активная |
| Динамическая пауза | Физ.минутка |
| Личностные: Формирование мотивации к ЗОЖ |
| Самостоятельное, творческое использование сформированных умений и навыков | Изучение нового материала осуществля-лось с использованием технологии критического мышления. Это дало возможность учащимися, используя логическое мышление, самостоятельно добывать знания. Все это помогло учащимся составить объемное и яркое представление по данной теме. На протяжении всего урока четко прослеживался принцип сотрудничества по схеме, ученик-учитель и учитель-ученик. | Регулятивные: -саморегуляция; - самооценка -коррекция (направленные на формирование контрольно-оценочной Д.) Коммуникативные: - формирование умения аргументировать свое высказывание Познавательные: -формирование умения строить логическую цепочку рассуждений Обратная связь: активная |
| Обобщение усвоенного учебного материала | После каждого этапа объяснения нового материала анализировались ответы учащихся, что способствова-ло закреплению и систематизации полученных знаний | Формы обучения Групповая Объект восприятия -речь учителя, -наглядные демонстрации Развитие познават.Д. - наглядно-образная память - словесно-логическая память; - абстрактное мышление -логическая память | Регулятивные: -саморегуляция; - самооценка -коррекция Коммуникативные: - формирование умения аргументировать свое высказывание, -степень самостоятельности Познавательные: -формирование умения структурировать знания Обратная связь: активная |
| Рефлексия |
| На уроке была предложена самостоятельная работа с компьютером с выхожом в сеть Интернет . | Регулятивные: -саморегуляция; - самооценка -коррекция Коммуникативные: -направленные на согласование усилий по достижению общей цели Познавательные: -рефлексия способов и условий действия, контроль и оценка процесса и результатов
|
| Гигиенические требования | Температурный режим, освещенность соответствовали нормам СанПиН |
|
|






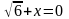 ; б)
; б) 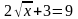 ; в)
; в) 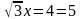 ;
; ; д)
; д) 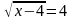 ?
?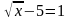 ; б)
; б) 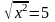 ; в)
; в) 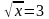 ; г)
; г) 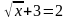 ; д)
; д) 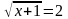 .
.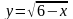 ; б)
; б) 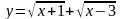 ; в)
; в) 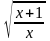 .
.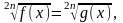 где n
где n 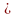 N,
N,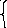
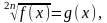 где n
где n 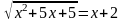
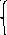
 х2+5х+5= х2+4х+4,
х2+5х+5= х2+4х+4, 









