Устный математический журнал "Грани математики". Выпуск №3. В мире четырехугольников.

Математический журнал

Грани математики. В мире четырехугольников.

Выпуск 3 ( январь- февраль)

Подготовила: Сороченко Анастасия Алексеевна

Руководитель: Мамасуева Татьяна Парфирьевна

Введение

В повседневной жизни нас постоянно окружают геометрические фигуры, а в особенности четырёхугольники, и чтобы узнавать их и не быть безграмотными в сфере геометрии надо знать четырёхугольники их виды и свойства, поэтому данная тема, по моему мнению, очень важна в любой момент времени. Данный материал также используется в тестовых заданиях ОГЭ, что важно для учащихся, чтобы успешно сдать экзамен.

Содержание проекта

• Определение четырёхугольника.
• Параллелограмм.
• Прямоугольник.
• Трапеция.
• Ромб.
• Квадрат.
• Использование четырёхугольников в задачах ОГЭ.
• Список используемой литературы.

Определение

Четырёхугольник  —  это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки. Основные виды четырехугольников: параллелограмм, прямоугольник, квадрат, ромб, трапеция.

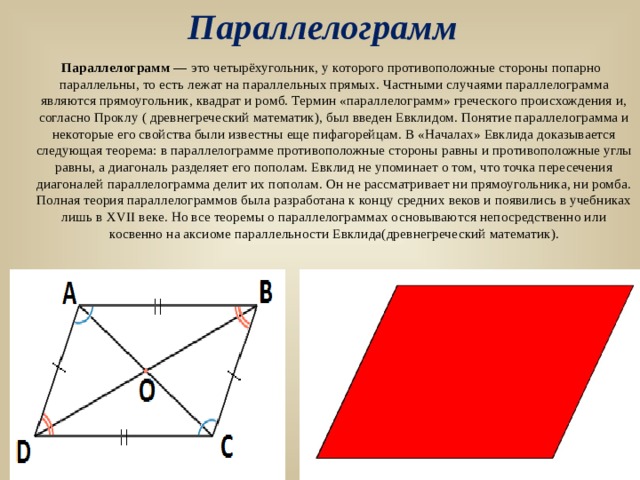
Параллелограмм

Параллелограмм  — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб. Термин «параллелограмм» греческого происхождения и, согласно Проклу ( древнегреческий математик), был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам. В «Началах» Евклида доказывается следующая теорема: в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам. Евклид не упоминает о том, что точка пересечения диагоналей параллелограмма делит их пополам. Он не рассматривает ни прямоугольника, ни ромба. Полная теория параллелограммов была разработана к концу средних веков и появились в учебниках лишь в XVII веке. Но все теоремы о параллелограммах основываются непосредственно или косвенно на аксиоме параллельности Евклида(древнегреческий математик).

Примеры использования параллелограмма в повседневной жизни

В строительстве

В запчастях и деталях (в рамах велосипедов)

В мебели (в подлокотниках на офисных креслах)

Прямоугольник

Прямоугольником  называется параллелограмм, у которого все углы прямые (равны 90 градусам). В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360°, прямоугольников не существует.

Примеры использования прямоугольника в повседневной жизни

Монитор

Предмет интерьера

Флаг

Трапеция

  «Трапеция» - слово греческое, означавшее в древности «столик» (по гречески - «трапедзион»).В средние века трапецией называли, по Евклиду, любой четырехугольник (не параллелограмм); лишь в XVIII в. это слово приобретает современный смысл, который встречаются впервые у древнегреческого математика Посидония. Предложение о том, что средняя линия трапеции равна полусумме ее основания, было известно древним египтянам, оно содержится в папирусе Ахмеса и фигурирует в виде инспекции (II в. до н. э.) на стенах храма Эдфу в Верхнем Египте. Это предложение было известно также вавилонским землемерам, оно содержится в трудах Герона Александрийского.

Примеры использования трапеции в повседневной жизни

В одежде

В мебели

В изделиях

В строительстве

Ромб

Термин «Ромб» происходит от латинского слова  rombus ( «ромбус») - формы греческого слова ῥόμβος («ромбос»), означающего бубен. Мы привыкли к тому, что сейчас бубен имеет круглую форму, но раньше он имел форму квадрата или ромба, о чём свидетельствуют изображения масти «бубны» на игральных картах.

Бубен

Раньше Сейчас

Ромб

Ромб - параллелограмм, у которого все стороны равны. Слово «ромб» впервые употребляет Герон Александрийский (греческий математик и механик второй половины I века ) и Папп Александрийский (древнегреческий математик второй половины III века).

Примеры использования ромба в повседневной жизни

В изделиях

В марках машин

В домкратах

В орнаментах

Квадрат

Квадрат  — правильный четырёхугольник, то есть четырёхугольник, у которого все углы и все стороны равны. Квадрат является одновременно частным случаем ромба и прямоугольника. Термин «квадрат» происходит от латинского quadratum- четырёхугольник (quadrare-сделать четырехугольным).«Первый четырехугольник, с которым познакомилась геометрия, был квадрат», - пишет Д. Д. Мордухай-Болтовский (1876-1952) - русский математик .

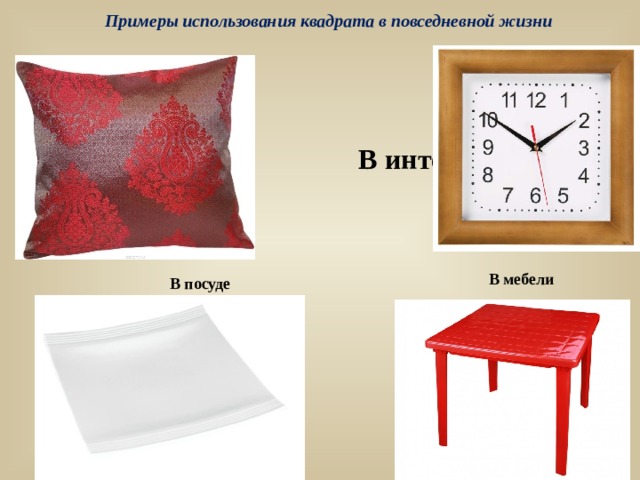
Примеры использования квадрата в повседневной жизни

В интерьере

В мебели

В посуде

Примеры использования квадрата в повседневной жизни

В интеллектуальных играх

Использование четырёхугольников в задачах ОГЭ

Использование четырёхугольников в задачах ОГЭ

Где мы можем увидеть четырёхугольники в повседневной жизни, а также столкнуться с ними?

Таким образом, можно сделать вывод, что четырехугольники встречаются в нашей жизни везде. Они могут “попасться” нам дома, а могут повстречаться на улице. Например: на улице мы можем встретить дом с прямоугольной дверью и квадратными окнами, а дома смотреть телевизор с прямоугольным экраном. Перечислять можно до бесконечности. Но, столкнувшись с ними, разве будем мы обращать внимание на то, что эти вещи имеют форму четырехугольника?

Список используемой литературы

•   ОГЭ-2019. Математика. Типовые экзаменационные варианты. 36 вариантов. Ященко И.В.
• https://studbooks.net/1962761/pedagogika/istoricheskaya_spravka_chetyrehugolnikah
• http://www.hintfox.com/article/chetirehygolniki-v-nashej-zhizni.html
• https://math-around.ru
• https://multiurok.ru/blog/primienieniie-v-zhizni-chietyriekhughol-nikov.html
• http://www.fipi.ru
• https://ru.wikipedia.org/wiki
• «Геометрия, 7-9 класс», авторы И.М. Смирнова, В.А. Смирнов
• «Геометрия, 7-11 класс», автор А.В. Погорелов
• «Геометрия, 7-9 класс», автор И.Ф. Шарыгин
• «Геометрия, 7-9 класс», автор Л.С. Атанасян
•   Геометрия для самообразования Выгодский М.Я.
• Геометрические места в пространстве и задачи на построение Наумович Н.В.   

Спасибо за внимание!