В мире формул сокращённого умножения

В МИРЕ ФОРМУЛ СОКРАЩЁННОГО УМНОЖЕНИЯ

7 КЛАСС

Составила

учитель математики и информатики

МОУ «СОШ №3 г. Зеленокумска», Ставропольского края

Касьянова Татьяна Валерьевна

Цитаты урока

«Математику нельзя изучать, наблюдая, как это делает сосед!»

А. Нивен

«Учиться можно только весело… Чтобы переварить знания, надо поглощать их с аппетитом.»

А. Франс

Ярмарка настроений

Отлич-

ное

Удовлет-

ворит.

Плохое

Хорошее

«Проверь себя»

«Найди меня»

2

2

1. b + 20b + * = (* + *) ;

b + 20b + 100 = (b + 10) .

2. * - 42pk + 49p = (* - *) ;

9k - 42pk + 49p = (3k – 7p) .

3.100m - 4n = (10m - *)(* + 10m );

100m - 4n = (10m - 2n )(2n + 10m ).

4.64x + * = (* + 3y)(* - 12xy + 9y );

64x + 27y = (4x + 3y)(16x - 12xy + 9y).

2

2

2

2

2

2

2

4

6

2

2

4

6

2

3

3

3

2

2

3

3

2

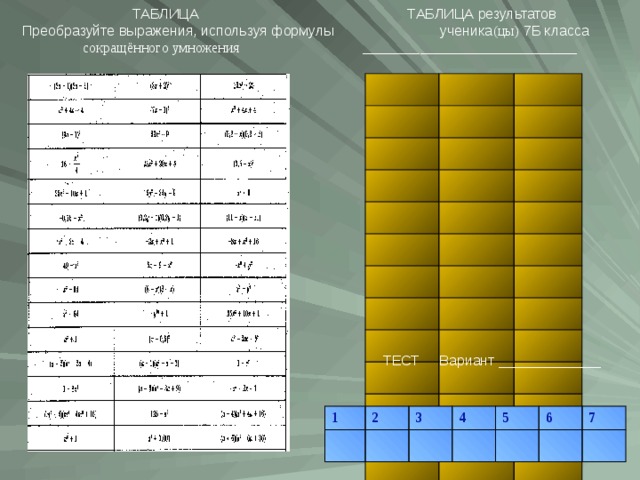
ТАБЛИЦА ТАБЛИЦА результатов

Преобразуйте выражения, используя формулы ученика (цы) 7Б класса

сокращённого умножения ______________________________

ТЕСТ Вариант _____________

1

2

3

4

5

6

7

Таблица результатов

2

2

4a – 1

(a + 2)

9x + 12x + 4

(4x – 5)(4x +5)

49x – 14x + 1

9a – 6a + 1

(x +2)

(7x – 3)(7x + 3)

(4 – x/2)(4 + x/2)

0,04 – x

(5x + 2)

(5x – 1)

(4y – 3)

(x – 0,04)(x + 0,04)

0,25 – x + x

(x – 3) + 6x

0,04y – 1

(x + 2)

(7 – x)(7 + x)

(x – 1)

121 – x

(x – 4)

(x + 3)

(x – 8)(x + 8)

(y – x)(y + x)

(x + 8) – 8x

64 – x

(1 – y )(1 + y )

(a + 1)(a - a +1)

(x + y) – 2xy

(5x +1)

x + x + 0,25

a – 8

- (a + b)

a + 1

(1 – 2x)(1 + 2x +4x )

(1 – с )(1 + с +с )

a + 27

m + 64

- (x + 1)

(5 –a)(25 + 5a + a )

(n + 1)(n – n +1)

(a+0,1)(a – 0,1a +0,01)

a – 64

a + 216

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

5

2

5

2

2

2

2

2

3

3

2

2

3

6

2

3

2

3

2

ОТЛИЧНО – 9 заданий ХОРОШО – 7 заданий УДОВЛЕТВОРИТЕЛЬНО – 5 заданий ПЛОХО – 3 задания

Ярмарка настроений

Отлич-

ное

Удовлет-

ворит.

Плохое

Хорошее

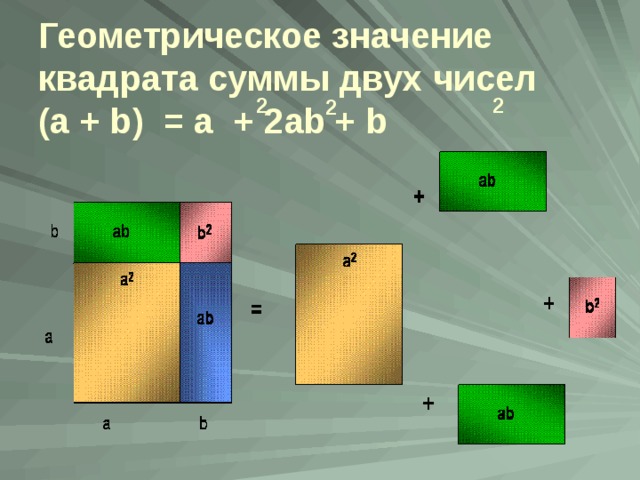
Геометрическое значение квадрата суммы двух чисел (a + b) = a + 2ab + b

2

2

2

Таинственный незнакомец «Арифметика»

«Поле чудес»

2

• 16y(2 – y) + (4y – 5) = 0
• 9x(x + 6) – (3x + 1) =1
• (6y+2)(5–y)=47–(2y–3)(3y–1)
• (x + 6) – (x - 5)(x + 5) = 79
• (2x – 3) – (7 – 2x) = 2
• (2 – х) – x(x + 1,5) = 4
• (x – 7) + 3 = (x – 2)(x + 2)

• 3 1/8 Д
• 1/24 И
• 2 О
• 1,5 Ф
• 2 5/8 А
• 0 Н
• 4 Т

2

2

2

2

2

2

ДИОФАНТ

Таинственный незнакомец

«Поле чудес»

• 12 – (4 – x) = x(3 – x)
• 8m (1 + 2m)–(4m + 3)(4m -3) = 3
• (2x – 3) – 2x(4 +2x) = 11
• (3x – 1)(2x +7)–(x +1)(6x – 5) = 7
• (8 – 9a)a +40 = (6 – 3a)(6 + 3a)

• 0.8 Э
• -0,75 Й
• -0,1 Л
• 0,5 Е
• -0,5 Р

2

2

ЛЕОНАРД ЭЙЛЕР

Ярмарка настроений

Отлич-

ное

Удовлет-

ворит.

Плохое

Хорошее

Примеры тестов

Ответы

5

6

Б

7

В

Г

ВАРИАНТ 1

6

7

В

Б

8

А

ВАРИАНТ 2

5

В

6

7

В

Б

ВАРИАНТ 3

5

Б

6

7

А

В

ВАРИАНТ 4

Ярмарка настроений

Отлич-

ное

Удовлет-

ворит.

Плохое

Хорошее

(a+b+c) =a +b +c +2ab+2ac+2bc

2

2

2

2

b

a

c

Найдите квадрат суммы следующих чисел:

(а – х + у) ;

(а – b – c) .

2

a

ac

ab

a

2

2

b

bc

ab

b

2

2

ac

c

bc

c

Обобщение утверждения

(a + b + c + … + k + m) =

= a + b + c + … + m +

+ 2ab + 2ac + … + 2km.

2

2

2

2

2

БЛЕЗ ПАСКАЛЬ

Рассмотрим двучлены:

ТАБЛИЦА

из их коэф-

фициентов

1

1 1

1 2 1

1 3 3 1

( a + b) = 1

(a + b) = a + b

(a + b) = a + 2ab + b

(a + b) = a + 3a b + 3ab +b

ЗАКОН образования коэффициентов?

0

1

2

2

2

3

3

2

2

3

Таблица

11 1 2

11 1 1 2

11 1 2 1 2

11 1 3 3 1 2

11 1 4 6 4 1 2

11 1 5 10 10 5 1 2

. . .

0

1

2

3

4

5

Найди ошибку!

• (4у – 3x)(3x + 4y) = 8y – 9x
• 100m – 4n = (10m – 2n )(10m + 2n )
• (3x + a) = 9x – 6aх +a
• (6a – 9 c) = 36a – 108a c + 18c

8y

2n

-6ax

18c

2

2

2

2

2

2

2

6

4

2

2

2

2

2

2

2

4

2

2

СОФИЗМ

Попробуем доказать равенство 4 = 5.

Рассмотрим две разности:

16 – 36 = 25 – 45.

Добавим число 81/4. Имеем:

16 – 36 + 81/4 = 25 – 45 + 81/4.

Представим эти выражения так:

4 – 2 * 4 * 9/2 + (9/2) = 5 – 2 * 5 * 9/2 + (9/2) .

Используем формулу

(4 – 9/2) = (5 – 9/2) .

4 – 9/2 = 5 – 9/2, 4 = 5. Где ошибка?

2

2

2

2

2

2

Ярмарка настроений

Отлич-

ное

Удовлет-

ворит.

Плохое

Хорошее

Итоги урока:

• встреча с упражнениями, при выполнении которых возникала необходимость использования формул;
• формулировка гипотезы и проверка её для различных частных случаев;
• обоснование для общего случая;
• оформление результатов;
• проверили уровень подготовки к контрольной работе.

Домашнее задание

• Изящные пирамиды чисел:

а) 1*8 + 1 = 9; 12*8 + 2 = 98; 123*8 + 3 = 987

Как дальше?

б) 1 = 1; 11 = 121; 111 = ?

• Возведите в степень:

а) (2а – b + c) ; б) (a + b) .

• Вычислите устно:

а) 976 ; б) 295 .

• Придумайте «доказательство» того, что 2=3

2

2

2

2

6

2

2