Вариант №1 теста ОГЭ

ВАРИАНТ 1

ЧАСТЬ 1

АЛГЕБРА

1. Найдите зна­че­ние вы­ра­же­ния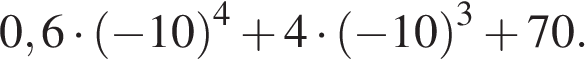 

2. В таб­ли­це при­ве­де­ны рас­сто­я­ния от Солн­ца до четырёх пла­нет Сол­неч­ной си­сте­мы. Какая из этих пла­нет дальше всех от Солн­ца?

1) Венера

2) Марс

3) Уран

4) Нептун

3. Числа  и  от­ме­че­ны точ­ка­ми на ко­ор­ди­нат­ной пря­мой. Рас­по­ло­жи­те в по­ряд­ке воз­рас­та­ния числа    и 1.

В ответе укажите номер правильного варианта.

1) 

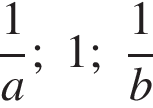
2) 

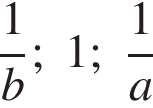
3) 

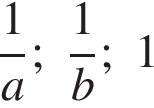
4) 

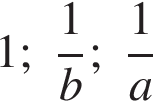
4. Найдите значение выражения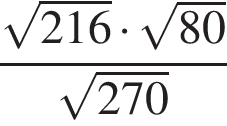 

1)

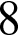
2)

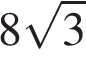
3)

4)

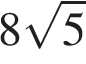
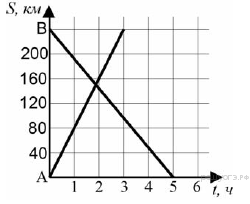
5. На ри­сун­ке изоб­ра­жен гра­фик дви­же­ния ав­то­мо­би­ля из пунк­та    в пункт    и ав­то­бу­са из пунк­та    в пункт  . На сколь­ко ки­ло­мет­ров в час ско­рость ав­то­мо­би­ля боль­ше ско­ро­сти автобуса?

6. Ре­ши­те урав­не­ние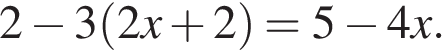 

7. На счет в банке, доход по ко­то­ро­му со­став­ля­ет 15% годовых, внес­ли 24 тыс. р. Сколь­ко тысяч руб­лей будет на этом счете через год, если ни­ка­ких опе­ра­ций со сче­том про­во­дить­ся не будет?

8. Завуч подвёл итоги кон­троль­ной ра­бо­ты по ма­те­ма­ти­ке в 9-х клас­сах. Ре­зуль­та­ты пред­став­ле­ны на диа­грам­ме.

Какое из утвер­жде­ний от­но­си­тель­но ре­зуль­та­тов кон­троль­ной ра­бо­ты верно, если всего в школе 120 де­вя­ти­класс­ни­ков?

  1) Более по­ло­ви­ны де­вя­ти­класс­ни­ков по­лу­чи­ли от­мет­ку "3".

2) Около по­ло­ви­ны де­вя­ти­класс­ни­ков от­сут­ство­ва­ли на кон­троль­ной ра­бо­те.

3) От­мет­ку "4" или "5" по­лу­чи­ла при­мер­но треть де­вя­ти­класс­ни­ков.

4) От­мет­ку "3", "4" или "5" по­лу­чи­ли более 100 уча­щих­ся.

9. На эк­за­ме­не 25 билетов, Сер­гей не вы­учил 3 из них. Най­ди­те ве­ро­ят­ность того, что ему попадётся вы­учен­ный билет.

10. Установите соответствие между функциями и их графиками.

 ФУНКЦИИ

  А)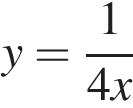 

Б)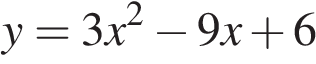 

B)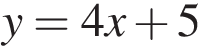 

 ГРАФИКИ

В таблице под каждой буквой укажите соответствующий номер.

11. Какое наи­боль­шее число по­сле­до­ва­тель­ных на­ту­раль­ных чисел, на­чи­ная с 1, можно сло­жить, чтобы по­лу­чив­ша­я­ся сумма была мень­ше 528?

12. Найдите зна­че­ние вы­ра­же­ния  при , 

13. Перевести зна­че­ние температуры по шкале Фаренгейта в шкалу Цельсия позволяет фор­му­ла , где — температура в гра­ду­сах Цельсия,— температура в гра­ду­сах Фаренгейта. Скольким градусам по шкале Цельсия соответствует 23 градуса по шкале Фаренгейта?

14. На каком рисунке изображено множество решений неравенства ?

ГЕОМЕТРИЯ

15. Картинка имеет форму прямоугольника со сторонами 14 см и 27 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 558 см. Какова ширина окантовки? Ответ дайте в сантиметрах.

16. На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 78°. Найдите угол CMA. Ответ дайте в градусах.

17.  Най­ди­те длину хорды окруж­но­сти ра­ди­у­сом 13 см, если рас­сто­я­ние от цен­тра окруж­но­сти до хорды равно 5 см. Ответ дайте в см.

18. На сто­ро­не BC пря­мо­уголь­ни­ка ABCD, у ко­то­ро­го AB = 3 и AD = 7, от­ме­че­на точка E так, что ∠EAB = 45°. Най­ди­те ED.

19. На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.

20. Какие из сле­ду­ю­щих утверждений верны?

1) Пра­виль­ный шестиугольник имеет шесть осей симметрии.

2) Пря­мая не имеет осей симметрии.

3) Цен­тром симметрии ромба яв­ля­ет­ся точка пе­ре­се­че­ния его диагоналей.

4) Рав­но­бед­рен­ный треугольник имеет три оси симметрии.

 Если утвер­жде­ний несколько, за­пи­ши­те их номера в по­ряд­ке возрастания.

ЧАСТЬ 2

АЛГЕБРА

21. Решите не­ра­вен­ство 

22. Све­жие фрук­ты со­дер­жат 80% воды, а вы­су­шен­ные — 28%. Сколь­ко сухих фрук­тов по­лу­чит­ся из 288 кг све­жих фрук­тов?

23. Постройте график функции  Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

ГЕОМЕТРИЯ

24. Отрезки AB и DC лежат на па­рал­лель­ных прямых, а от­рез­ки AC и BD пе­ре­се­ка­ют­ся в точке M. Най­ди­те MC, если AB  = 16, DC  = 24 , AC  = 25.

25. В па­рал­ле­ло­грам­ме ABCD диа­го­на­ли AC и BD пе­ре­се­ка­ют­ся в точке M. До­ка­жи­те, что пло­щадь па­рал­ле­ло­грам­ма ABCD в че­ты­ре раза боль­ше пло­ща­ди тре­уголь­ни­ка AMB.

26. Боковые сто­ро­ны AB и CD тра­пе­ции ABCD равны со­от­вет­ствен­но 8 и 10, а ос­но­ва­ние BC равно 2. Бис­сек­три­са угла ADC про­хо­дит через се­ре­ди­ну стороны AB. Най­ди­те площадь трапеции.

ОТВЕТЫ

21. Решите не­ра­вен­ство 

Решение.

Преобразуем неравенство:

Произведение двух мно­жи­те­лей меньше нуля тогда и толь­ко тогда, когда мно­жи­те­ли имеют раз­ный знак, поэтому:

Ответ: 

22. Све­жие фрук­ты со­дер­жат 80% воды, а вы­су­шен­ные — 28%. Сколь­ко сухих фрук­тов по­лу­чит­ся из 288 кг све­жих фрук­тов?

Решение.

Свежие фрук­ты со­дер­жат 20% пи­та­тель­но­го вещества, а вы­су­шен­ные — 72%. В 288 кг све­жих фрук­тов со­дер­жит­ся 0,2 · 288 = 57,6 кг пи­та­тель­но­го вещества. Такое ко­ли­че­ство пи­та­тель­но­го ве­ще­ства будет со­дер­жать­ся в  кг вы­су­шен­ных фруктов.

 Ответ: 80.

23. Постройте график функции  Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

Решение.

Раскрывая модуль, получим, что функ­цию можно пред­ста­вить сле­ду­ю­щим образом:

 Этот гра­фик изображён на рисунке:

 Из гра­фи­ка видно, что пря­мая  имеет с гра­фи­ком функ­ции ровно две общие точки при  и 

 Ответ: −0,25; 6,25.

24.  Отрезки AB и DC лежат на па­рал­лель­ных прямых, а от­рез­ки AC и BD пе­ре­се­ка­ют­ся в точке M. Най­ди­те MC, если AB  = 16, DC  = 24 , AC  = 25.

Решение.

Углы DCM и BAM равны как на­крест лежащие, углы DMC и BMA равны как вертикальные, следовательно, тре­уголь­ни­ки DMC и BMA подобны по двум углам. Значит,

Следовательно,

  от­ку­да 

Ответ: 15.

25. В па­рал­ле­ло­грам­ме ABCD диа­го­на­ли AC и BD пе­ре­се­ка­ют­ся в точке M. До­ка­жи­те, что пло­щадь па­рал­ле­ло­грам­ма ABCD в че­ты­ре раза боль­ше пло­ща­ди тре­уголь­ни­ка AMB.

Решение.

Проведём вы­со­ту  так, чтобы она про­хо­ди­ла через точку Углы  и  равны друг другу как вертикальные. Вспом­ним также, что диа­го­на­ли де­лят­ся точ­кой пе­ре­се­че­ния пополам, следовательно,  Рас­смот­рим тре­уголь­ни­ки  и , они прямоугольные, имеют рав­ные углы и рав­ные гипотенузы, сле­до­ва­тель­но эти тре­уголь­ни­ки равны, а зна­чит равны от­рез­ки  и . Таким образом, 

Площадь па­рал­ле­ло­грамм равна  а пло­щадь тре­уголь­ни­ка 

 26. Боковые сто­ро­ны AB и CD тра­пе­ции ABCD равны со­от­вет­ствен­но 8 и 10, а ос­но­ва­ние BC равно 2. Бис­сек­три­са угла ADC про­хо­дит через се­ре­ди­ну стороны AB. Най­ди­те площадь трапеции.

Решение.

Введём обо­зна­че­ния как по­ка­за­но на рисунке. Про­дол­жим бис­сек­три­су до пе­ре­се­че­ния с пря­мой  в точке  Углы  и  равны как на­крест ле­жа­щие при па­рал­лель­ных прямых. Значит, следовательно, тре­уголь­ник  — равнобедренный: Найдём  Углы  и  равны как вертикальные. Рас­смот­рим тре­уголь­ни­ки  и  сто­ро­ны  и равны, углы  и  равны как вертикальные, углы  и  равны как на­крест ле­жа­щие при па­рал­лель­ных прямых, следовательно, эти тре­уголь­ни­ки равны, от­ку­да  Проведём пря­мую  па­рал­лель­ную  Пря­мая  па­рал­лель­на  пря­мая  па­рал­лель­на  следовательно, четырёхугольник  — параллелограмм, от­ку­да  Найдём  Рас­смот­рим тре­уголь­ник  заметим, что

Следовательно, по теореме, об­рат­ной тео­ре­ме Пифагора, получаем, что тре­уголь­ник  — прямоугольный, следовательно,  — вы­со­та трапеции. Найдём пло­щадь трапеции:

Ответ: 40.

6