Векторыурок-обобщение по геометрии в 9 кл.

Векторы урок-обобщение по геометрии в 9 кл.

Оглавление

• Понятие вектора
• Коллинеарные векторы
• Сонаправленные векторы
• Противоположно направленные векторы
• Равные векторы
• Противоположные векторы
• Сложение векторов
• Вычитание векторов ( I )
• Вычитание векторов (II)
• Произведение вектора на число

Понятие вектора

Многие физические величины (сила, скорость, ускорение) характеризуются не только числовым значением, но и направлением в пространстве. Такие физические величины называют векторными величинами .

Понятие вектора

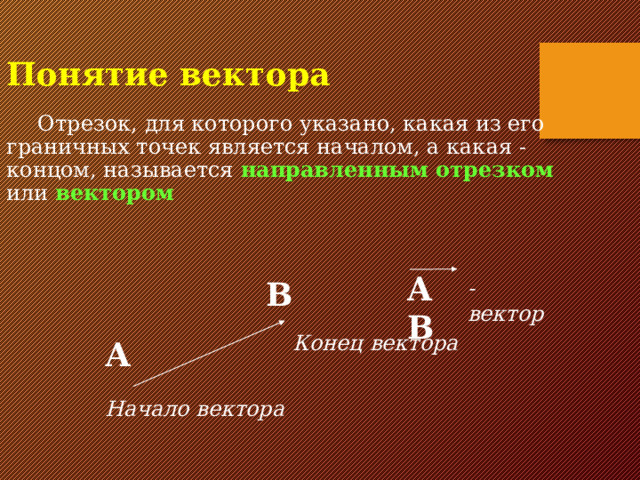
Отрезок, для которого указано, какая из его граничных точек является началом, а какая - концом, называется направленным отрезком или вектором

AB

- вектор

В

Конец вектора

А

Начало вектора

4

Коллинеарные векторы

Ненулевые векторы называются коллинеарными , если они лежат на одной прямой или на параллельных прямых

a||b, b||c, a||c

c

a

b

Нулевой вектор считается коллинеарным любому вектору

5

Сонаправленные векторы

Сонаправленные векторы – это векторы, которые коллинеарны и имеют одинаковые направления.

d

a b, b d, a d

a

c

b

6

Противоположно направленные векторы

Противоположно направленные векторы – это векторы, которые коллинеарны и имеют разное направление.

d

a c, b c, d c

a

c

b

7

Длина вектора

Е

Длиной вектора или модулем ненулевого вектора называется длина отрезка

К

| КЕ | = | KE | длина вектора КЕ

М

| ММ | = 0

Равные векторы

Равные векторы – это сонаправленные векторы, имеющие одинаковые длины.

b

a=b : 1) a b

2) |a|=|b|

a

9

Противоположные векторы

Противоположные векторы – это противоположно направленные векторы, имеющие одинаковые длины.

b

a = - b : 1) a b

2) |a| = |b|

a

Сложение векторов Правило треугольника

Дано: a, b

a

b

Построить: c = a + b

Построение:

a

b

a + b = c

c

11

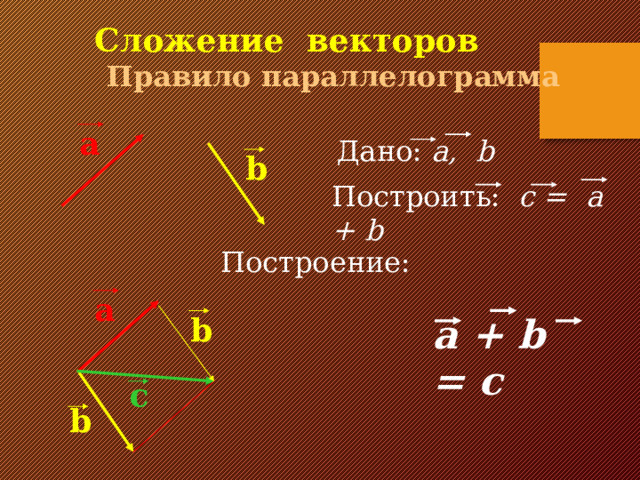
Сложение векторов Правило параллелограмма

a

Дано: a, b

b

Построить: c = a + b

Построение:

a

a + b = c

b

c

b

12

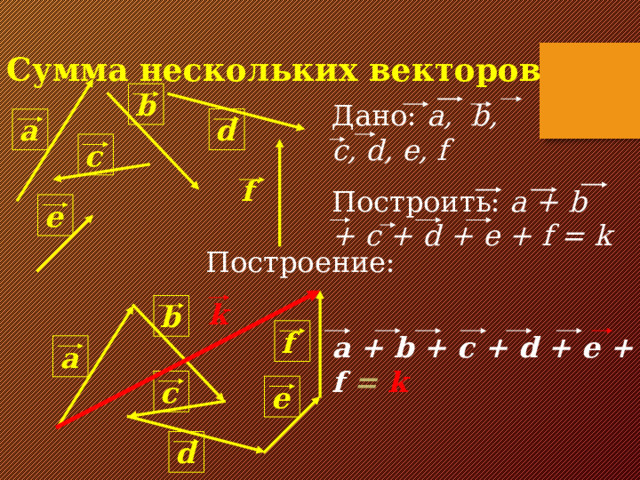
Сумма нескольких векторов

b

Дано: a, b , с , d, e, f

d

a

c

f

Построить: a + b + c + d + e + f = k

e

Построение:

k

b

f

a + b + c + d + e + f = k

a

c

e

d

13

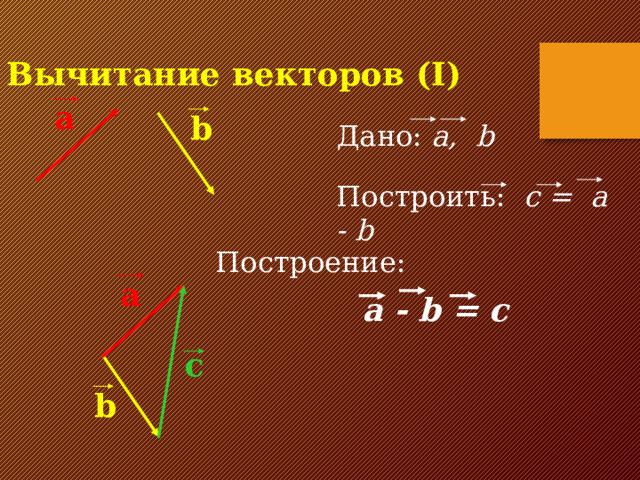
Вычитание векторов (I)

a

b

Дано: a, b

Построить: c = a - b

Построение:

a

a - b = c

c

b

14

a - b = c c - b " width="640"

Вычитание векторов ( II )

a

b

Дано: a, b

Построить: c = a - b

Построение:

a

a + (- b ) = c =

a - b = c

c

- b

0, то a ↑↑ b если k 0, то a ↑↓ b Произведение любого вектора на нуль есть нулевой вектор a 2 a -2 a Для любых чисел k , l и любых векторов a, b справедливы равенства: 1 º . ( k l ) a = k ( la ) (сочетательный закон), 2 º . ( k + l ) a = k a + la (первый распределительный закон), 3 º . k ( a + b ) = k a + kb (второй распределительный закон). 16 " width="640"

Произведение вектора a на число k

k· a = b

• если k 0, то a ↑↑ b
• если k 0, то a ↑↓ b
• Произведение любого вектора на нуль есть нулевой вектор

a

2 a

-2 a

Для любых чисел k , l и любых векторов a, b справедливы равенства:

1 º . ( k l ) a = k ( la ) (сочетательный закон),

2 º . ( k + l ) a = k a + la (первый распределительный закон),

3 º . k ( a + b ) = k a + kb (второй распределительный закон).

16