Вездесущая теорема

Эта вездесущая теорема Пифагора.

Выполнил: Малышев Илья ученик 7 «а» класса, 2019г.

Историческая справка:

Треугольник одна из древних геометрических фигур.

Первые упоминания о треугольнике и его свойствах ученые находят в египетских папирусах, которым более 4000 лет.

В Древней Греции изучение свойств треугольника достигает высокого уровня – это теорема Пифагора и формула Герона, которым более 2000 лет.

Очень много лет, и даже столетий, прошло с тех пор, как Пифагор сделал своё открытие. Люди использовали его и в древности, и в средневековье, и продолжают использовать и в наше время.

В данном исследовании я попытался изучить самые разные стороны применения теоремы Пифагора. Кроме этого, узнал больше о личности Пифагора, заинтересовался различными доказательствами этой теоремы и попробовал её использовать в своей практике.

Цели и задачи проекта:

Цель: Выяснить, как применяется теорема Пифагора на практике.

Задачи: Найти исторические сведения о

Пифагоре.

Изучить теорему Пифагора и её доказательства.

Узнать, как теорема Пифагора применяется в жизни.

Применить полученные знания в своей

практике.

Становление математики как теоретической науки связано с Пифагором и его последователями в 5 в. до н. э. Именно Пифагор первым понял, что истинность утверждений необходимо доказать, прежде чем они могут быть использованы в дальнейших логических рассуждениях. Для этого Пифагор использовал основополагающий элемент философии – логику.

Успех пифагореизма легко понять. Пифагор был современником Будды (563-483 или 623-543 гг. до. н. э.), Конфуция (551-479 гг. до н. э.) и Лао-цзы ( 6 или 5 в. до н. э.), также являвшихся основателями собственных учений, в которых трудно определить, где заканчивается религия и начинается философия. Пифагорейское учение оказалось идеальным синтезом мистики и рационального мышления, смесью науки и религии, которая предлагала совершенный образ жизни. Пифагор начал излагать своё ученик на Самосе, своём родном острове, в возрасте 40 лет. Перед этим философ долгое время путешествовал. Он был в Египте и в Вавилоне, посетив, по некоторым данным, и Индию.

Пифагор

Древнегреческий философ и математик

(580 - 500 г. до н.э.)

Пифагор — это не имя, а прозвище, данное ему за то, что он высказывал истину так же постоянно, как дельфийский оракул (Пифагор означает «убеждающий речью». Этимология связывает наречение с культом Апполона Пифийского).

Пифагор – одна из самых загадочных фигур в истории. Имеющаяся о нём информация не вполне достоверна, так как больше похожа на легенды, чем на факты. Историки, которые писали о нём, жили сотни лет спустя. Официально считается,

что Пифагор родился около 570 г. до н. э. на острове Самосе в Эгейском море, у берегов современной Турции. По версии некоторых авторов он был сыном Аполлона, другие считают, что его отец – богатый островитянин Мнесарх. Считается, что Пифагор жил в крупнейших центрах древних цивилизаций, в том числе в Египте и в Персии, где он изучал литературу, религию, философию и математику. Вероятно, он прожил 20 лет в Вавилоне, где учился и преподавал астрономию, математику и астрологию. Позже он вернулся на родину. Считается, что он отправился в Египет, где продолжил учёбу. Как бы то ни было, мы знаем наверняка, что он в конце концов поселился в Кротоне на юге Италии.

После смерти Пифагор стал мифической фигурой: ему приписывали чудеса и магические способности, что сделало его наиболее интересной и загадочной личностью в истории человечества. Однако строгий обет молчания, принятый его последователями, и обязательство никогда не разглашать результаты изысканий имели печальные последствия. Это препятствовало распространению открытий пифагорейцев среди широкой общественности и вызывало больше подозрения относительно их деятельности. Поэтому сегодня всё, что мы знаем о Пифагоре, основывается на трудах других авторов, живших поколениями позже его, не всегда беспристрастных и восхвалявших своего героя и великого мудреца. Письменных источников было чрезвычайно мало. Таким образом, знания передавались от одного поколения к другому устно. Кроме того, из уважения к Пифагору ему почти всегда приписывались все открытия его учеников и последователей. Поэтому

нет ни подлинных свидетельств открытий, ни доказательств того, что все свои результаты Пифагор получил сам.

Теорема Пифагора.

Теорема Пифагора - важнейшее утверждение

геометрии.

Теорема формулируется следующим образом:

площадь квадрата, построенного на

гипотенузе прямоугольного треугольника,

равна сумме площадей квадратов,

построенных на его катетах.

Открытие этого утверждения приписывают Пифагору Самосскому

(XII в. до н. э.)

Изучение вавилонских клинописных табличек и древних китайских

рукописей (копий еще более древних манускриптов) показало,

что знаменитая теорема была известна задолго до Пифагора,

возможно несколько тысячелетий до него.

(Но есть предположение, что Пифагор дал ее полноценное

доказательство)

Доказ атель ство Пифагора

a

b

Дано:

Прямоугольный треугольник

а, в  – катеты

с - гипотенуза

Доказать :

с 2 =а 2 +b 2

Доказательство:

1) Достроим треугольник до квадрата со

стороной  а + в.

2) S=  (а+в) 2

S= 4∙1/2ав+с 2 =2ав+с 2

Тогда,  2ав+с 2 =(а+в) 2

2ав +с 2 =а 2 + 2ав +в 2

Вычтем из обеих частей  2ав,  тогда:

с 2 =а 2 +в 2 , что и требовалось доказать.

b

a

c

c

c 2

c

c

a

b

a

b

a

b-a

b

a

Еще один алгебраический способ доказательства теоремы.

Доказательство Бхаскара (XII в.)

(b-a) 2 +41/2ab=c 2

b

c

b 2 -2ab +a 2 +2ab =c 2

(b-a) 2 +4*1/2ab=c 2

b 2 +a 2 =c 2

10

Доказательство Леонардо да Винчи

Гениальный Леонардо да Винчи (1452 - 1519) нашёл блестящее доказательство теоремы Пифагора. Он изобразил треугольник с тремя квадратами на сторонах, добавив ещё две части: треугольник ECF сверху и равный исходному треугольник J I H снизу. Проведя перпендикулярные отрезки DG и CI, он заметил, что DG симметрично делит пополам шестиугольник ABDEFG. Если нижнюю из этих частей повернуть( вокруг точки A), то она покроет ровно половину шестиугольника ACBJ I H. Отсюда следует, что сумма площадей двух квадратов на катетах должна быть такой же, как площадь квадрата на гипотенузе.

Другое красивое доказательство из

арабского текста Аннаирици

( около 900 г. до н. э.)

основано на мозаике.

Мозаика состоит из кусочков квадратов,

соответствующих катетам,

наложенных на квадрат,

соответствующий гипотенузе.

Обе мозаики покрывают одну

и ту же поверхность.

Удивительно оригинальный

способ доказательства теоремы!

Моё доказательство

2

2

45

Широкое применение имеет при решении  геометрических  задач.

Найти S ABCD

B

30

A

C

4

Н.Ф. Гаврилова «Поурочные разработки по геометрии: 8 класс»

S ABCD = S ABC + S ADC

S ABCD = 2 + 8

D

14

13

12

13

На стороне АВ АВСD , равной 12 см, отмечена точка М так, что МС = 13 см. Найдите площадь четырехугольника АМСD .

12

В

С

1) 13 2 – 12 2 = 169 – 144 = 25, = 5(см).

2) S 12 2 = 144(см).

M

S

Б.Г. Зив, В.М Мейлер «Дидактические материалы по геометрии. 8 класс».

3) S AMCD = S - S

S AMCD = 144 - 30 = 114(см).

А

D

12

15

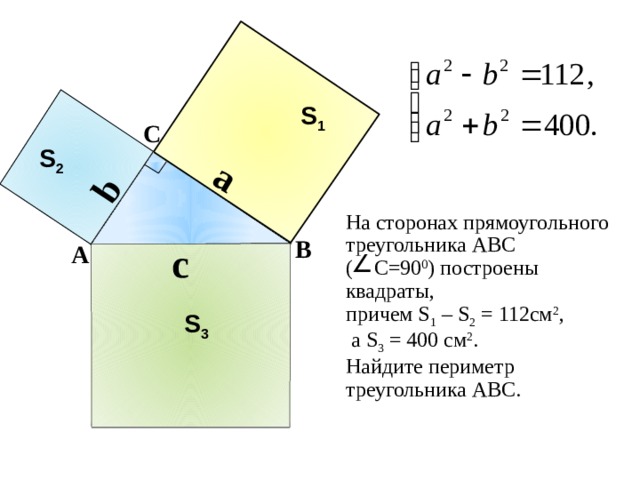
a

b

S 1

С

S 2

На сторонах прямоугольного треугольника АВС

( С=90 0 ) построены квадраты,

причем S 1 – S 2 = 112см 2 ,

а S 3 = 400 см 2 .

Найдите периметр треугольника АВС.

В

A

c

S 3

П.И. Алтынов «Геометрия. Тесты. 7-9 кл.»

16

Решение:

1) = 112 +

2) + = 400

112 + + = 400

= 400 – 144

2 = 400 – 112

= 256

2 = 288

= 16 (см)

= 288 : 2

= 144

b = 12 (см)

3) c = 20 (см)

4) Р = 12 + 16 + 20 = 48 (см)

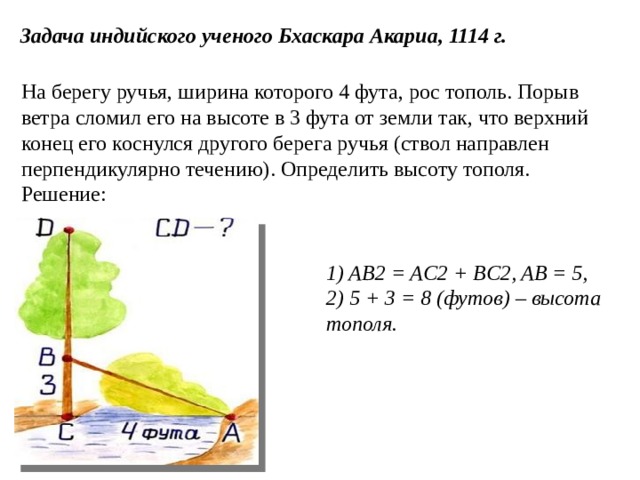
Задача индийского ученого Бхаскара Акариа, 1114 г.

На берегу ручья, ширина которого 4 фута, рос тополь. Порыв ветра сломил его на высоте в 3 фута от земли так, что верхний конец его коснулся другого берега ручья (ствол направлен перпендикулярно течению). Определить высоту тополя.

Решение:

1) AB2 = AC2 + BC2, AB = 5,   2) 5 + 3 = 8 (футов) – высота тополя.

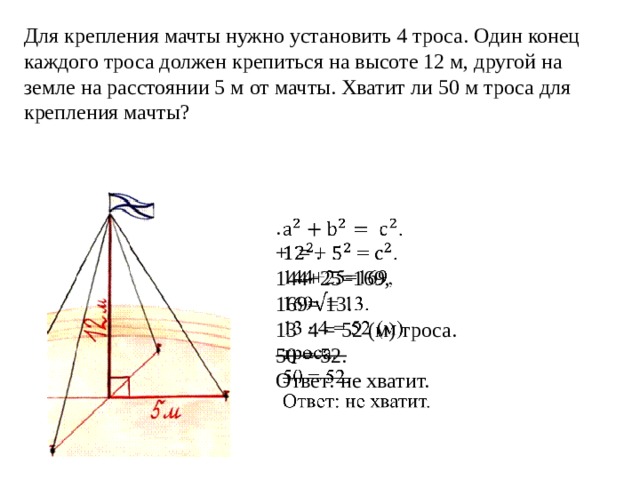
Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?

.

+ = .

144+25=169,

169= 13.

13 4 = 52 (м) троса.

50 = 52.

Ответ: не хватит.

Задача из учебника «Арифметика» Леонтия Магницкого:

«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».

= + .

125 = + 117

= - .

= 125 – 117.

= 8.

Существует бесчисленное множество целых положительных чисел,

удовлетворяющих соотношению

с 2 = а 2 + b 2 .

Они называются Пифагоровыми числами.

3 2 + 4 2 = 5 2

5 2 + 12 2 = 13 2

7 2 + 24 2 = 25 2

9 2 + 40 2 = 41 2

Треугольник со сторонами 3, 4 и 5 часто называют египетским треугольником

т. к. он был известен еще древним египтянам.

11 2 + 60 2 = 61 2

Каждый треугольник, стороны которого относятся, как 3:4:5 – прямоугольный, т.к. 3 2 +4 2 =5 2

13 2 + 84 2 = 85 2

6 2 + 8 2 = 10 2

9 2 + 12 2 = 15 2

12 2 + 16 2 = 20 2

21

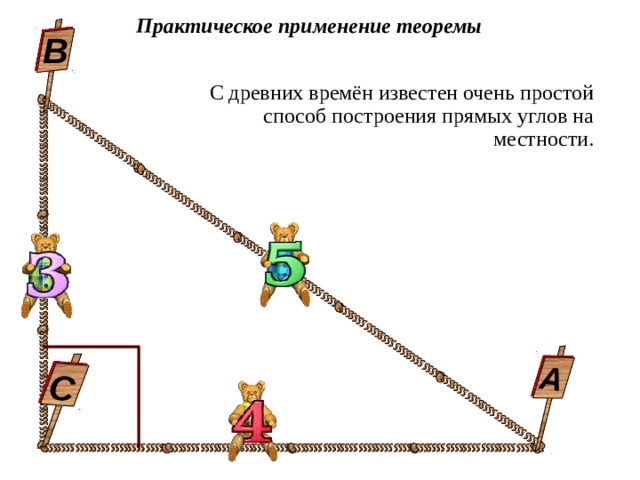
С

А

Практическое применение теоремы

В

С древних времён известен очень простой способ построения прямых углов на местности.

По мнению крупнейшего немецкого историка математики

М. Кантора 1829 — 1920),

(в Древнем Египте существовала особая профессия гарпедонаптов — «натягивателей веревок»,

которые во время торжественной церемонии закладки храмов и

пирамид размечали прямые углы с помощью веревки, имеющей

12 (= 3 + 4 + 5) равноотстоящих узлов.

На изображении видим три разных круга с радиусами, равными сторонам

прямоугольного треугольника.

Площадь большого круга = Площадь среднего круга + Площадь круга поменьше.

25

16

+

9

=

+

4

3

5

=

Площадь круга радиусом 5 = Площадь круга радиусом 4 + Площадь круга радиусом 3.

Теорема Пифагора позволяет находить соотношение площадей любых подобных фигур.

+ 30 см 30 см В теорему Пифагора можно подставлять абсолютно любые цифры. Она может помочь нам и в повседневной жизни. Например, мы никак не можем выбрать: заказать большую пиццу диаметром 50 см или две диаметром 30 см? Мы с теоремой уже знакомы хорошо и нас не обмануть: площадь одной пиццы в 50 см будет действительно больше, чем площадь двух пицц по 30 см в диаметре. " width="640"

+

30 см

30 см

В теорему Пифагора можно подставлять абсолютно любые цифры. Она может помочь нам и в повседневной жизни. Например, мы никак не можем выбрать: заказать большую пиццу диаметром 50 см или две диаметром 30 см? Мы с теоремой уже знакомы хорошо и нас не обмануть: площадь одной пиццы в 50 см будет действительно больше, чем площадь двух пицц по 30 см в диаметре.

Теорема Пифагора широко применяется в строительстве, архитектуре и мобильной связи.

При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки.

h

b/2

При строительстве лестниц необходимо рассчитать длину, ширину каждой ступени, крутизну лестницы.

При строительстве мостов, дорог рассчитывают подъемы и спуски.

Я измерил высоту и ширину крыши. Известно, что молниеотвод защищает все предметы, расстояние до которых не превышает его удвоенной высоты, т.е. c 2h, h c : 2.

a = 5 м, b = 4 м.

c = 2a + b2+ = 52 + 42 = 41 м.

h 41 : 2 6,4 : = 3,2 м.

h

c

a

b

На открытом пространстве расстояние до видимого горизонта зависит от высоты точки наблюдения над земной поверхностью. Ученые вывели

формулу расстояния до горизонта S2=(R+h)2-R2 , где R – радиус земли, а h – высота объекта применяется.

Мой рост 1,75. Я просчитал, что видимое мною расстояние до горизонта примерно равно 4,722 км.

При R Земли = 6371 км.

В мобильной связи

В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе.

Вывод:

Выдающимся вкладом в математику является теорема Пифагора, устанавливающая связь между квадратом, построенным на гипотенузе прямоугольного треугольника, и квадратами, построенными на его катетах. Как и все гениальное, теорема Пифагора отличается не только изысканной простой и массой геометрических приложений, но и имеет огромное число интерпретаций в самых различных областях математики, начиная от векторной алгебры и кончая теорией рядов Фурье и функциональным анализом.

Спасибо за внимание!