1. Понятие неопределенного интеграла
Если функция f(x) определена и непрерывна на промежутке (a,b) и F(x) -её первообразная, т.е. F’(x)=f(x) при axb , то
 , axb
, axb
где C - произвольная постоянная.
Основные свойства неопределенного интеграла:
1.  1.2.2.
1.2.2. 
2. 
3. 
Таблица простейших интегралов:
1. 
2. 
3. 
4. 
5. 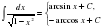
6. 
7.  ,
,  ;
; 
8. 
9. 
10. 
11. 
2. Интегрирование простейших неопределенных интегралов
Рассмотрим несколько примеров нахождения интегралов с помощью использования основных свойств неопределенного интеграла и таблицы простейших интегралов.
 =
=
=  =
=  =
=
= 27 =
= 
 =
=
= 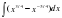 =
=  =
= 
3. Интегрирование методом преобразования
Для нахождения следующих интегралов надо выполнить некоторые преобразования подинтегрального выражения. Продемонстрируем этот прием на конкретных примерах.
 =
=  =
=  =
=  -
- =
=  .
.
 =
=  =
=  =
=  +С.
+С.
Аналогично берутся интегралы:
 ,
,  ,
,
 ,
,  ,
,
 ,
,
4. Интегрирование с применением подходящей подстановки
Метод подстановки: если f(x) непрерывна, то, полагая
 ,
,
где  непрерывная вместе со своей производной
непрерывная вместе со своей производной  , получим
, получим
 .
.
Продемонстрируем этот прием на конкретных примерах.
 =
=
=  =
=  =
=  =
=  .
.
 =
=
=  =
=  =
=  +С.
+С.
Аналогично берутся интегралы:
 ,
,  ,
,
 ,
,  ,
,
 ,
,  .
.
В следующих номерах формула нового аргумента не является линейной.
 =
=  =
= =
=  =
=  .
.
 =
=  =
=  .
.
 =
=  =
=  .
.
 =
=  =
=  = -
= -
 .
.
 =
=  =
=  =
=  +С.
+С.
 =
=  =
=  =
=  =
=
=  .
.
Аналогично, подбирая подходящие нелинейные подстановки, можно решить
 ,
,  ,
,
 ,
, 

 ,
,
 ,
, 
 ,
,  .
.
5. Решение интегралов вида
 ,
,  ,
,  ,
, 
Рассмотрим решение этих интегралов в общем виде.
 =
=  =
=  .
.
 =
=  =
=  =
=  .
.
 =
=  =
=  =
=  =
=
=  .
.
 =
=  =
=  .
.
Теперь нетрудно разобрать решение некоторых конкретных интегралов.
 =
=  = =
= =  .
.
 = =
= =  .
.
 =
=  =
=  =
=  =
=  =
=  =
=  .
.
 =
=  = sgnx
= sgnx = -sgnx
= -sgnx  =
=
= -sgnx .
.
 =
=  =
=  =
=  =
= 
Аналогично берутся следующие интегралы:
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
6. Интегрирование по частям
Метод интегрирования по частям: если u и v некоторые дифференцируемые функции от x , то
 .
.
Рассмотрим на нескольких примерах возможности метода интегрирования по частям.
 =
=  =
=  =
= 
Иногда, чтобы взять интеграл, приходится применять интегрирование по частям несколько раз.
 =
=
=  =
=  =
=
=  =
=  =
=
= 
Бывает, что приходится применять интегрирование по частям несколько раз, чтобы получить уравнение относительно заданного интеграла.
 =
=
=  =
=  +
+ =
=
=  =
=  +
+ -
-
Решая полученное относительно заданного интеграла уравнение
 =
=  +
+ -
- ,
,
вычисляем интеграл.
 =
=  +С
+С
Этим же методом решаются
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
7. Интегрирование с помощью выделения полного квадрата
Ранее уже разбиралось решение интегралов вида  ,
,  ,
,  ,
,  . Добавим к ним новые:
. Добавим к ним новые:  ,
,  и
и  . Приведем решение новых интегралов в общем виде.
. Приведем решение новых интегралов в общем виде.
 =
=  =
=  .
.
 =
=  =
=  =
=
=  =
=  ,
,
т.о.  =
=  .
.
 =
=  =
=  =
=
=  =
= ,
,
т.о.  =
= .
.
Выделяя полный квадрат и используя полученные формулы, найдем некоторые конкретные интегралы.
 =
=  =
=  =
=  .
.
 =
=  =
=  +
+ =
=
=  +
+ .
.
Аналогично решаются указанные ниже интегралы.
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
8. Интегрирование методом неопределенных коэффициентов
Этот метод основан на том, что, как известно из алгебры, любая рациональная дробь представляется в виде суммы многочлена и правильной рациональной дроби. А правильная рациональная дробь раскладывается на сумму элементарных дробей. Т.о., если подинтегральная функция есть рациональная дробь, то, используя аддитивность интеграла, достаточно вычислить сумму интегралов от каждого слагаемого в отдельности.
Продемонстрируем этот метод на решении.

Представим  рациональную дробь
рациональную дробь  , являющуюся подинтегральной функцией, в виде суммы многочлена и правильной рациональной дроби:
, являющуюся подинтегральной функцией, в виде суммы многочлена и правильной рациональной дроби:
 =
=
Затем разложим получившуюся правильную дробь на сумму элементарных дробей, знаменатели которых есть сомножители получившейся правильной дроби, а числители имеют степень на единицу меньше степени знаменателя и содержат неопределенные коэффициенты.
 =
=  =
=  =
=  =
=  .
.
Т.о.  =
=  .
.
Сравнивая числители двух разных представлений одной и той же дроби, точнее говоря, сравнивая коэффициенты при неизвестной в разных её степенях, получаем систему двух линейных уравнений с двумя неизвестными: a и b.
 Получили систему
Получили систему  . Её решение есть
. Её решение есть 
Вычислить значения коэффициентов можно и другим способом. Присмотримся к уравнению

Подставляя в него  , получаем
, получаем  , или
, или  .
.
При  получаем
получаем  , или
, или  .
.
Т.о. имеем
 =
=
= =
= .
Аналогично решаются нижеследующие интегралы.
 ,
,  ,
,
 ,
,  ,
,
 ,
,  .
.
9. Интегрирование иррациональных выражений
Для интегрирования иррациональных функций необходимо привести их к функциям рациональным. Рассмотрим несколько конкретных примеров, в которых это можно сделать.
 =
=  =
=  =
=  =
=  =
=
=  .
.
 =
=  =
=
=  =
=  =
=  =
=
=  .
.
Аналогично решаются нижеследующие интегралы.
 ,
,  ,
,
 ,
,  ,
,
 ,
,  .
.
Вычисление интегралов вида  ,
,  ,
,  и
и  рассматривалось ранее.
рассматривалось ранее.
Векторы на плоскости
а) Координаты вектора

б) Разложение вектора по координатным осям.

Действия над векторами

Длина вектора ,заданного координатами точек

Длина вектора ,заданного своими координатами

Скалярное произведение двух векторов
а)
б) 
Угол между векторами

Общее уравнение прямой
Ax + By + C=0
Частные случаи общего уравнения прямой
| Значение коэффициента | Вид уравнения | Положение прямой |
| С = 0 A = 0 B = 0 A = C = 0 B = C = 0 | Ax + By = 0 (y = kx) By + C = 0 (y = b) Ax + C = 0 (x = a) Y = 0 X = 0 | Через точку (0;0) Параллельна ОХ Параллельна ОY Совпадает с ОХ Совпадает с OY |
Векторное уравнение прямой



Пусть l – прямая плоскости XOY
(.) M0 (x0; y0) (.) M (x; y)

Вектор  - нормальный вектор
- нормальный вектор

Скалярное произведение 
Векторное произведение в координатной форме

Каноническое уравнение прямой

Направляющий вектор  (m; n)
(m; n)
Уравнение прямой, проходящей через две заданные точки
(.) A (X1; Y1) (.) B (X2; Y2)

Условие параллельности двух прямых
Прямые заданы уравнением 

k1 = k2
Прямые заданы координатами точек
(.) A (X1; Y1) (.) B (X2; Y2
 ;
;
 ,
, 

Условие перпендикулярности двух прямых
k1 · k2 = -1 m1m2 + n1n2 = 0
Образец решения практической работы
Задание 1.
Дано: (.) А (4; 0) (.) B (7; 4) (.) C (-4; 6)
а) Найти Р треугольника АВС
б) Найти cos A; угол А
в) Написать уравнение медианы, проходящей через (.) А
г) Уравнение высоты AN
д) Составить каноническое уравнение прямой ВС
е) Составить уравнение прямой, проходящей через (.) B || AC
Решение
а) Найти периметр треугольника АВС





б) Найдем косинус угла 
Угол А = 90°
в) Составим уравнение медианы АМ :
точка М – середина ВС
координаты точки найдем по формуле


Координаты точки А (4;0) ; координаты точки M ( ; 5)
; 5)




Составим уравнение прямой, проходящей через точки А и М
 ; решая его, найдем уравнение
; решая его, найдем уравнение

y = -2 (x - 4) = -2x + 8
y= -2x + 8 уравнение прямой АМ
) Уравнение высоты AN:
Дано: (.) А (4; 0) (.) B (7; 4) (.) C (-4; 6)
Построим треугольник и проведем высоту из вершины А
найдем координаты вектора АN.Для этого выпишем координаты
точки А (4; 0) и точки N (х; у)
Найдем координаты вектора АN

Решая уравнение получаем y= 5,5x – 22 - уравнение высоты
д) Составить каноническое уравнение прямой ВС
(.) В (7; 4) (.) C (-4; 6)


е) Составить уравнение прямой, проходящей через (.) B || AC
 - направляющий вектор
- направляющий вектор
(.) В (7; 4)







 , axb
, axb  1.2.2.
1.2.2. 






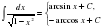

 ,
,  ;
; 




 =
= =
=  =
=  =
= 
 =
=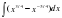 =
= 
















