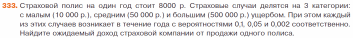ПРИМЕРНЫЙ СЦЕНАРИЙ УРОКА
РАЗДЕЛ «МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ»
11КЛАСС
Тема «Примеры применения математического ожидания
(страхование, лотерея)»

Урок составлен на основе:
Экспериментального учебного пособия для 10 и 11 классов Теория вероятностей и статистика. / Ю.Н. Тюрин, А.А.Макаров, И. Р.Высоцкий, И. В. Ященко. ––М.: МЦНМО, 2014.
Сайта Математическая вертикаль | Вероятность в школе
Учебного пособия Бунимович Евгений Абрамович. Математика. Вероятность и статистика : 11-й класс : базовый и углублённый уровни : учебное пособие / Е. А. Бунимович, В. А. Булычев. — Москва : Просвещение, 2023
РАЗДЕЛ: МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ (4 Ч.)
Урок 1. Примеры применения математического ожидания (страхование, лотерея)
Основные задачи уроков: Познакомить учащихся с примерами применения математического ожидания.
Примерный план проведения урока:
Математическое ожидание играет важную роль в области математической статистики и теории вероятностей. Оно представляет собой среднее значение случайной величины и помогает предсказать, какие значения можно ожидать в будущем. Математическое ожидание находит применение во многих сферах — от физики и экономики до компьютерных наук и биологии.
Предположим, у нас есть случайная величина X. Её математическое ожидание можно обозначить как E(X) или EX.
Пусть распределение случайной величины X задано таблицей.
| Значение величины X | x1 | x2 | x3 | x4 | ….. | xn |
| Вероятность | p1 | p2 | p3 | p4 | ….. | pn |
Определение:
| Математическим ожиданием случайной величины X называют число EX=x1⋅p1+x2⋅p2+x3⋅p3+...+xn⋅pn. |
Математическое ожидание случайной величины, которая имеет измеряемые значения в определённых единицах, также будет измеряться в указанных единицах. Например, для случайной величины «вес» математическое ожидание будет выражено в килограммах, а для случайной величины «рост» — в сантиметрах. Это связано с тем, что значения случайной величины и её математического ожидания согласуются в одних и тех же единицах измерения.
Задание 1. Подбрасывают игральный кубик. Случайная величина X — число очков, выпавших на кубике.
Найдём математическое ожидание E(X). Вероятность выпадения каждой грани одинакова и равна 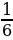
Следовательно, EX=1⋅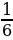 +2⋅
+2⋅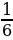 +3⋅
+3⋅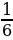 +4⋅
+4⋅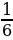 +5⋅
+5⋅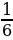 +6⋅
+6⋅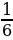 =
=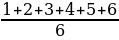 =3,5.
=3,5.
Представим ситуацию, в которой каждое значение случайной величины имеет одинаковую вероятность появления. В таком случае математическое ожидание можно определить как просто среднее арифметическое всех значений. Этот пример наглядно демонстрирует эту концепцию.
Найдём математическое ожидание выигрыша, рассмотрев пример с расчётом цены лотерейного билета.
Задание 2. Для проведения лотереи было изготовлено 200 билетов, из которых один билет имеет выигрыш в размере 1000 рублей, 20 билетов имеют выигрыш в размере 1500 рублей, а остальные билеты не имеют выигрышей. Для определения выигрыша выбирается один билет случайным образом.
Эта случайная величина может принимать три значения: 1000, 1500 и 0 руб. (нет выигрыша). Их вероятности равны: 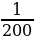 =0,005,
=0,005, 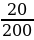 =0,1 и
=0,1 и 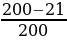 =
=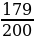 =0,895.
=0,895.
Тогда математическое ожидание выигрыша равно
EX=1000⋅0,005+1500⋅0,1+0⋅0,895= 155 руб.
Получается, что средний выигрыш на один билет равен 155 рублей.
Для того чтобы обеспечить доходы организаторов, лотерея должна иметь более высокую цену билета, чем средний выигрыш.
Такова особенность всех лотерей и конкурсов: математическое ожидание выигрыша на один билет меньше стоимости самого билета.
Это условие является обязательным и гарантирует прибыльность конкурсов и лотерей, а также доход для их организаторов. Любой человек, решивший поучаствовать в лотерее, должен осознавать это и сознательно рисковать своими финансами.
Игры, в которых математическое ожидание выигрыша больше, требуют большего количества игр для получения значительного дохода устроителя лотереи. Такая игра привлечёт меньше людей, если математическое ожидание меньше.
Однако необходимо помнить, что для любой лотереи требуется специальное разрешение (лицензия). Устраивать игры без лицензии является нарушением закона, а сам устроитель является мошенником. В такие игры нельзя играть!
Рассмотрим пример, который демонстрирует использование математического ожидания для определения стоимости страхового полиса ОСАГО.
Полис ОСАГО обязателен для всех владельцев автомобилей и предназначен для покрытия гражданской ответственности. Его можно приобрести у страховых компаний, которые берут на себя обязательство в случае ДТП возместить ущерб, который автовладелец причинит окружающим.
В Государственной Думе проходили обсуждения стоимости полиса и пределов выплат.
Для определения стоимости полиса необходимо знать две величины: вероятность, с которой автовладелец может причинить ущерб окружающим в результате ДТП в течение года, и среднюю сумму ущерба. Перемножение этих величин позволяет получить средний размер страховой премии компании на один застрахованный автомобиль.
Каждая выплата для отдельного автомобиля является случайной величиной. Стоимость полиса состоит из математического ожидания страховой выплаты и дохода страховой компании.
Задание 3. Страховой полис ОСАГО в страховой компании стоит 35000 рублей. По статистике в течение года владелец автомобиля попадает в мелкую аварию с вероятностью 0,15, и средняя сумма страховой выплаты при этом равна 50000 рублей. С вероятностью 0,027 автомобиль попадает в серьёзную аварию, и средняя сумма выплаты при этом будет 600000 рублей.
Найдём математическое ожидание случайной величины «средняя сумма страховой выплаты»:
50000⋅0,15+600000⋅0,027 = 23700 руб.
Найдём «средний доход страховой компании от продажи одного полиса», зная, что страховой полис ОСАГО стоит 35000 руб.:
35000−23700 = 11300 руб.
Задание 4. Закон распределения вероятностей дискретной случайной величины дан в виде таблицы. Найти математическое ожидание этой величины.
| Х | – 4 | – 3 | – 2 | – 1 | 0 | 1 | 2 | 3 | 4 |
| Р | 0,02 | 0,03 | 0,1 | 0,15 | 0,4 | 0,15 | 0,1 | 0,03 | 0,02 |
E(Х)=-4⋅0,02+(-3)⋅0,03+(-2)⋅0,1+(-1)⋅0,15+0⋅0,4+1⋅0,15+2⋅0,1+3⋅0,03+4⋅0,02=0
Задание 5. На рынке куплены одинаковые по размеру лимоны: 3 лимона – по 20 руб. за штуку, 12 лимонов – по 10 руб. за штуку. Найти математическое ожидание стоимости одного лимона
E(Х)=20 ⋅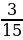 +10⋅
+10⋅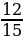 =
=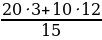 =
= =12
=12
Задание 6. Для проведения лотереи изготовили 100 билетов. Из них 1 билет с выигрышем 500 рублей, 10 билетов по 100 руб. и остальные по 5 рублей (беспроигрышная лотерея). Наудачу выбирают билет. Найти математическое ожидание выигрыша.
Желательный результат обсуждения: Для того чтобы лотерея приносила доход, цена билета должна быть больше, чем средний выигрыш, например 30 руб. (Доход 3000 – 1945 = 1055 руб.).
Отдельный игрок может и выиграть, но в конечном итоге доход будет у организатора лотереи.
E(Х)=500⋅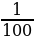 +100⋅
+100⋅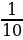 +5⋅
+5⋅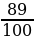 =
=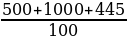 =19,45
=19,45
Задание 7. Подбрасывают два кубика. Случайная величина S — сумма очков, выпавших на кубиках. Найдите математическое ожидание E(S).
Вспомним её закон распределения:
| Значения S | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Вероятность | 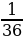
| 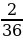
| 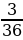
| 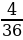
| 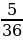
| 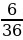
| 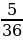
| 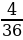
| 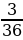
| 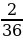
| 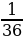
|
Желательный результат обсуждения:
E(S) =2⋅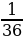 +3⋅
+3⋅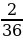 +4⋅
+4⋅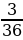 +5·
+5·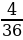 +6
+6 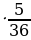 +7
+7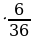 +8
+8 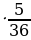 +9·
+9·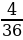 +10⋅
+10⋅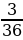 +11⋅
+11⋅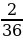 + +12⋅
+ +12⋅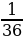 =
=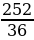 =7
=7
Мы получили ответ 7, который можно было угадать и без вычислений — ведь распределение вероятностей симметрично относительно значения 7.
Это свойство мы рассмотрим на следующем примере и построим полигон
.
Задание 8. Нужно найти математическое ожидание случайной величины X, имеющей следующее распределение вероятностей
| Значения Х | 1 | 2 | 4 | 6 | 8 | 9 |
| Вероятность | 0,012 | 0,152 | 0,336 | 0,336 | 0,152 | 0,012 |
Е(Х)=1⋅ 0,012 +2⋅0,152+4⋅0,336+6⋅0,336+8⋅0,152+9⋅0,012=5
Построим полигон математического ожидания
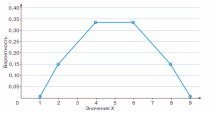
Из таблицы и рисунка хорошо видно, что распределение симметрично относительно точки 5, поэтому E(X) = 5. Обратите внимание, что сама эта точка не является одним из значений случайной величины — это требование вовсе не обязательно.
Домашнее задание: В качестве домашнего задания можно предложить
задания из учебника Бунимович Евгений Абрамович. Математика. Вероятность и статистика : 10-й класс : базовый и углуб лённый уровни : учебное пособие / Е. А. Бунимович, В. А. Булычев. — Москва : Просвещение, 2023
Стр.198-199 №№331,333
Здесь для удобства представлены скрины номеров


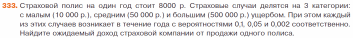
Презентация к уроку находится по ссылке Загрузка страницы (vk.com)








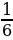
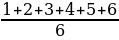 =3,5.
=3,5.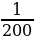 =0,005,
=0,005, 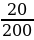 =0,1 и
=0,1 и 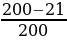 =
=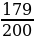 =0,895.
=0,895. 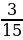 +10⋅
+10⋅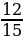 =
=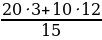 =
= =12
=12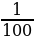
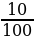
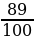
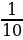 +5⋅
+5⋅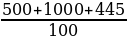 =19,45
=19,45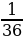
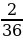
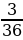
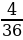
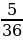
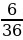
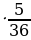 +7
+7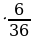 +8
+8 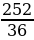 =7
=7