Вариант № 2 1 часть. Модуль «Алгебра»
1. Найдите значение выражения: 
| Мощность автомобиля (в л. с.*) | Налоговая ставка (в руб. за л. с. в год) |
| не более 70 | 0 |
| 71—100 | 12 |
| 101—125 | 25 |
| 126—150 | 35 |
| 151—175 | 45 |
| 176—200 | 50 |
| 201—225 | 65 |
| 226—250 | 75 |
| свыше 250 | 150 |
2. В таблице представлены налоговые ставки на автомобили в Москве с 1 января 2013 года.
*л. с. — лошадиная сила
Сколько рублей должен заплатить владелец автомобиля мощностью 162 л. с. в качестве налога за один год?
В ответе укажите номер правильного варианта.
1) 45 2) 50 3) 7290 4) 6750
3. На координатной прямой точками отмечены числа 

Какому числу соответствует точка C?
1) 2)
2) 3)
3) 4)
4)
4. Какое из данных чисел является значением выражения  ? 1)
? 1) 2)
2) 3)
3) 4)
4)
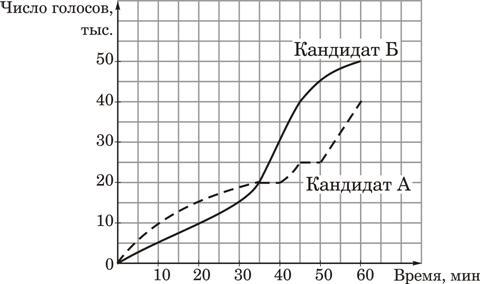
5. На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего телезрителей проголосовало к 40-й минуте дебатов?
6. Найдите корни уравнения 
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
7. В начале учебного года в школе было 840 учащихся, а к концу года их стало 966. На сколько процентов увеличилось за год число учащихся?
8. Рок-магазин продаёт значки с символикой рок-групп. В продаже имеются значки пяти цветов: чёрные, синие, зелёные, серые и белые. Данные о проданных значках представлены на столбчатой диаграмме.
Определите по диаграмме, значков какого цвета было продано меньше всего. Сколько примерно процентов от общего числа значков составляют значки этого цвета?
1) 5 2) 10 3) 15 4) 20
9. У бабушки 10 чашек: 9 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
10. На рисунках изображены графики функций вида  . Установите соответствие между знаками коэффициентов
. Установите соответствие между знаками коэффициентов  и
и  и графиками функций.
и графиками функций.
КОЭФФИЦИЕНТЫ
А)  Б)
Б)  В)
В) 
ГРАФИКИ

В таблице под каждой буквой укажите соответствующий номер.
11. Последовательность задана формулой  Сколько членов в этой последовательности больше 6?
Сколько членов в этой последовательности больше 6?
12. Найдите значение выражения  при
при 
13. Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 70 см, n =1400 ? Ответ выразите в километрах.
14. Решите неравенство .
В ответе укажите номер правильного варианта.
1) 2) 3) 4)
1 часть. Модуль «Геометрия»
15. Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча, когда конец длинного плеча поднимается на 1,8 м?
16. Катеты прямоугольного треугольника равны  и 1. Найдите синус наименьшего угла
и 1. Найдите синус наименьшего угла
17. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA = 5°. Найдите угол NMB. Ответ дайте в градусах.
18. В прямоугольном треугольнике один из катетов равен 10, угол, лежащий напротив него, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на  .
.
19 . Найдите тангенс угла , изображённого на рисунке.
20. Укажите номера верных утверждений.
1) Существует ромб, который не является квадратом.
2) Если две стороны треугольника равны, то равны и противолежащие им углы.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.
2 часть. Модуль «Алгебра»
21. Сократите дробь
22. Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?
23. При каких положительных значениях  прямая
прямая  имеет с параболой ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
имеет с параболой ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
2 часть. Модуль «Геометрия»
24. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M иN соответственно. Найдите BN, если MN = 14, AC = 21, NC = 10.
25. В треугольнике  угол
угол  равен 36°, — биссектриса. Докажите, что треугольник
равен 36°, — биссектриса. Докажите, что треугольник  — равнобедренный.
— равнобедренный.
26. Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите этот диаметр, если диаметр описанной окружности треугольника ABC равен 8.




















