МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «УЗНИМАХИНСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА»
Внеклассное мероприятие
по геометрии в 8 классе
Тема: По следам Пифагора 
Провела:
учитель математики
МКОУ "Узнимахинская СОШ"
Кадиева З. К.
Цель: Закрепить и расширить знания учащихся теоремы и биографии Пифагора.
Развивать интеллектуальные навыки: сравнение, классификация, анализ.
Развивать коммуникативные навыки и математическую речь.
Воспитывать диалоговую культуру.
Воспитывать любовь к предмету.
Оборудование: раздаточный материал, проектор.
Ход занятия:
I. Организационный момент.
а) приветствие
б) проверка готовности к уроку.
II Основная часть.
1) Сообщение темы и цели.
Учащимся предлагается разгадать кроссворд, а ключом к разгадыванию кроссворда будут правильные ответы на вопрос учителя.
1. Как называются стороны прямоугольного треугольника?
 (катеты и гипотенуза).
(катеты и гипотенуза).
2. Каким является катет ВС по отношению к углу А? (противолежащим)
3. Как называется отношение прилежащего катета к гипотенузе? (Косинусом острого угла прямоугольного треугольника).
4. Каким является катет АС по отношению к углу А? (прилежащим)
5. От чего зависит косинус угла? (от градусной меры).
6. Задача. На стороне угла ВАС отложены равные отрезки по5см.
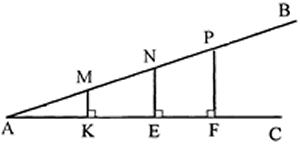
Из точек М, N, Р к стороне АС проведены перпендикуляры MK, NE, PF. Расстояние АК=4 см.
Найти: из МАК cosA ,NAE cosA, PAF cosA
Решение: т.к. 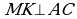 ,
, 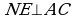 и
и 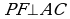 , то
, то 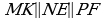 .
.
На основании теоремы Фалеса имеем: AK=KE=EF=4cm. Из МАК имеем: cosA=AK/AM; cosA=4/5
NAE имеем: cosA=AE/AN, cosA=8/10=4/5
APAF имеем: cosA=AF/AP, cosA=12/l5=4/5
Вопрос: Что можно сказать о значении косинуса угла А?
Ответ: Не зависит от размеров треугольника, а зависит только от градусной меры угда.
Вопрос: Какую теорему использовали при доказательстве равенства длин отрезков, т.е. AK=KE=EF?
Ответ: Теорему Фалеса.
- обратите внимание на то, что при разгадывании кроссворда, получим слово, «Пифагор».
тему занятия: «Теорема Пифагора».
«Во мгле веков пред нашим взором
Блеснула истина одна.
Она, как теорема Пифагора
До наших дней еще верна».
| г | п |
|
|
|
|
|
| и | р |
| к |
| к | п |
| п | и | ф | а | г | о | р |
| о | л | а | т | р | с | о |
| т | е | л | е | а | и | т |
| е | ж | е | т | д | н | и |
| н | а | с |
| у | у | в |
| у | щ |
|
| с | с | о |
| з | и |
|
|
|
| л |
| а | й |
|
|
|
| е |
|
|
|
|
|
|
| ж |
|
|
|
|
|
|
| а |
|
|
|
|
|
|
| щ |
|
|
|
|
|
|
| и |
|
|
|
|
|
|
| й |
2) Устная разминка.
А) 1 Какие треугольники называются, прямоугольными?
2 Как называются стороны прямоугольного треугольника?
3 Как сравнить катеты и гипотенузу?
4 Чему равна сумма острых углов прямоугольного треугольника?
Б) тест
1. Какой треугольник называется прямоугольным? Как называются его стороны? (катеты, гипотенуза лежит против угла в 90°)
2. Продолжите предложение: В прямоугольном треугольнике любой катет
а) равен гипотенузе;
б) меньше гипотенузы;
в) больше гипотенузы;
г) определить нельзя.
3. В прямоугольном треугольнике один из острых углов равен 20°.Найдите второй острый угол. (90°-20°=70°)
4. Один из катетов прямоугольного треугольника равен половине гипотенузы, острые углы равны:
а) 60° и 30°;
б) по 45°;
в) однозначно определить нельзя.
В). Решите устно задачи по чертежу.
Найдите неизвестную сторону треугольника. 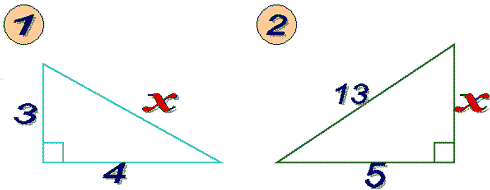
-Как иначе называют треугольник со сторонами 3, 4 и 5? (египетским).
ответ к задаче 2: х2=132-52 = 144 , х=12 )
3) Выступление учеников.
Учитель: Молодцы, а сейчас мы с вами заслушаем реферат и узнаем интересные факты из жизни Пифагора.
Историческая справка.
Пифагор родился на острове Самос, приблизительно в 580г. до нашей эры в семье богатого купца Мнесарха. Долгое время жил в Египте, по некоторым данным (т.к. для всей литературы о Пифагоре характерна полнейшая недостоверность), в Вавилоне.Известно, что в молодости он много путешествовал по дальним странам: египетские жрецы обучали его геометрии, вавилоняне – арифметике и астрономии, персидские – маги тайным обрядам и жертвоприношению.
На родине взгляды Пифагора не встретили сочувствия, поэтому он переехал на юг Италии в город Кротон, где основал свой союз. Он начал преподавать свое собственное учение, привлекая к себе множество слушателей. Здесь же возникла пифагорейская школа. Своим ученикам Пифагор преподавал три главных предмета: математику, музыку и учение о переселении душ. Эти три предмета составляли единую науку о космосе и космической гармонии. Рассказывают, что он своими глазами видел стройное движение небесных сфер и слышал их гармоническую мелодию. Пифагор первым назвал вселенную космосом, т.е. миром украшенным или прекрасно устроенным. Предания рисуют Пифагора чудотворцем, волшебником – говоря по-нашему. Рассказывали, что он предвидел землетрясения, укрощал волны, останавливал эпидемии, беседовал с животными. Число- Пифагор считал тем чудесным инструментом, и с помощью которого был сотворен космос. «В основе всех вещей – числа» - говорил он. Отцом и матерью Мира он называл единицу и двойку. По учению Пифагора единица – знак светлой божественной энергии, а двойка – знак темной, мертвой стихии. И ныне, покупая на день рождения нечетное число цветов, а на похороны – четное, мы соблюдаем, не ведая того – это древнее правило Пифагора. Имя древнегреческого математика Пифагора пользуется уважением и в наше время. На родине, в Греции, выпущена почтовая марка с его изображением. Его именем названа одна из улиц в Амстердаме, расположенная по соседству с улицами Архимеда, Ньютона, Коперника. В последние годы остров Самос переименован в остров Пифагореум.
4) Доказательство теоремы Пифагора.
«Давным-давно на белом свете
Та теорема рождена.
Но нет и места на планете,
Где б неизвестною была.
Как символ вечного союза,
Как верной дружбы знак простой,
Связала ты, гипотенуза
Навеки катеты с собой.
А катет говорит гипотенузе
Сдружились мы с тобой навеки крепко.
И ссориться не будем мы с тобою никогда
Сковал нас Пифагор давно и цепко.
«Теорема Пифагора».
Теорема: Во всяком прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
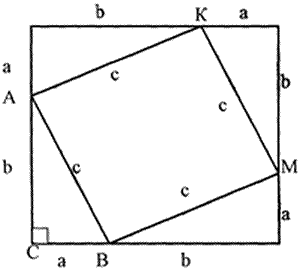
Дано: АВС, угол С=90°. АС, СВ – катеты, АВ – гипотенуза.
АС=b; СВ=а; АВ=с.
Доказать: а2 +b2 =с2
Доказательство: Достроим АВС до квадрата.
Получим четыре равных прямоугольных треугольника (по 2-м катетам), отсюда следует, что гипотенузы равны. Четырехугольник АВМК – ромб.
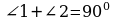 т.к. АВС - прямоугольный.
т.к. АВС - прямоугольный.
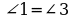 ^l, следовательно,
^l, следовательно, 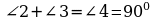
Если у ромба есть угол 90°, то такой ромб является квадратом: АВМК –квадрат.
Sб.кв.=(a+b)2=a2+2ab+b2
Sб.кв.=4S +SABKM= 4l/2ab +c2 =2ab+c2.
Имеем: a2+2ab+b2=2ab+c2, т.е. a2+b2=c2
Теорема доказана.
- Существует более 150 видов доказательств данной теоремы. Но и сейчас еще стремление к умножению этих доказательств не исчезло. Поэтому у вас есть еще возможность дать свое доказательство этой теоремы.
IV Домашнее задание.
Пифагорова головоломка.
Из семи частей квадрата составить снова прямоугольник. Квадрат разрезается так: Е, F, К, L – середины сторон квадрата, О - центр квадрата, 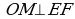 ,
, 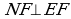
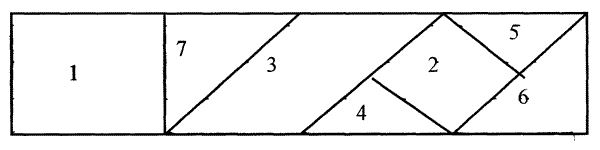








 (катеты и гипотенуза).
(катеты и гипотенуза).
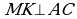 ,
, 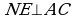 и
и 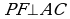 , то
, то 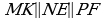 .
.

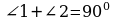 т.к. АВС - прямоугольный.
т.к. АВС - прямоугольный.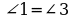 ^l, следовательно,
^l, следовательно, 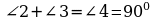
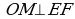 ,
,