Геометрия 7 класс
Тема: ВНЕШНИЙ УГОЛ ТРЕУГОЛЬНИКА.
Теорема о внешнем угле треугольника
Цели:
– закрепить знания учащихся о сумме углов треугольника при решении задач;
– ввести понятие внешнего угла треугольника;
– доказать теорему о внешнем угле треугольника;
– решение задач по теме урока.
Ход урока
I. Проверка усвоения изученного материала.
1. Один учащийся на доске доказывает теорему о сумме углов треугольника.
2. Второй учащийся решает на доске задачу № 230.
3. Устно со всем классом решаем задачи по готовым чертежам (раздаточный материал находится на каждой парте у обучающихся).
Вычислите все неизвестные углы треугольника (по рис. 1–8).
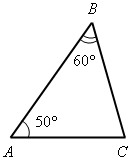

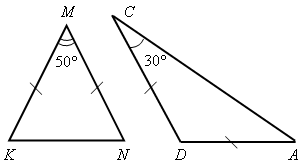
Рис. 1 Рис. 2 Рис. 3 Рис. 4
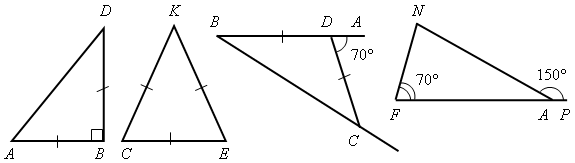
Рис. 5 Рис. 6 Рис. 7 Рис. 8
II. Изучение нового материала.
1. Ввести понятие внешнего угла треугольника.
Определение
Внешним углом треугольника называется угол, смежный с внутренним углом данного треугольника.
В
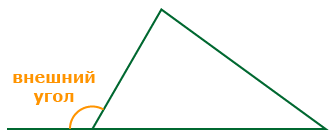
D А С
∠BAD – внешний угол при вершине A треугольника ΔАВС.
При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ΔABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:
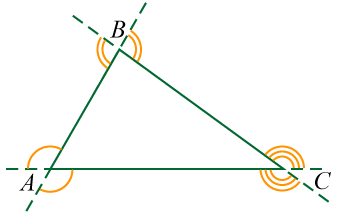
2. Доказать теорему о внешнем угле треугольника.
Теорема.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
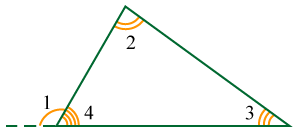
Доказательство:
Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°: ∠1 + ∠4 = 180°.
Сумма внутренних углов любого треугольника тоже равна 180°, значит: ∠2 + ∠3 + ∠4 = 180°.
Из этого следует, что ∠1 + ∠4 = ∠2 + ∠3 + ∠4.
Сократив обе части полученного равенства на одно и тоже число (∠4), получим: ∠1 = ∠2 + ∠3.
Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.
Записать в тетрадях свойство:
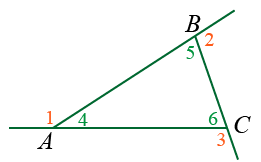
Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360:
| 
|
∠1 + ∠2 + ∠3 = 360°. |
3. Устно решить задачу:
В треугольнике АВС ∠В = 110°.
Чему равны:
а) сумма остальных внутренних углов треугольника?
б) внешний угол при вершине В?
4. По готовому чертежу на доске устно решить задачу:
| 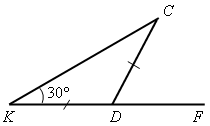
| Найдите: – внутренние углы треугольника ΔKСD; – внешний угол ∠СDF .
|
III. Решение задач.
1. Решить задачу № 232 под руководством учителя на доске и в тетрадях.
| 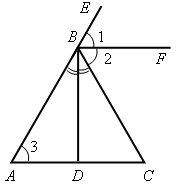
| Дано: ∠CВE – внешний угол треугольника ΔАВС; ∠CВE = 2∠А. Доказать: ΔАВС – равнобедренный
|
Доказательство
Проведем биссектрисы BF и ВD смежных углов ∠СВЕ и ∠АВС, тогда ВF  ВD.
ВD.
ВF || АС, так как ∠1 = ∠2 = ∠3, а углы ∠1 и ∠3 соответственные при пересечении прямых ВF и АС секущей АВ.
ВD  АС, так как ВD
АС, так как ВD  ВF, а ВF || АС. В треугольнике ΔАВС биссектриса ВD является высотой, следовательно, треугольник ΔАВС – равнобедренный.
ВF, а ВF || АС. В треугольнике ΔАВС биссектриса ВD является высотой, следовательно, треугольник ΔАВС – равнобедренный.
2. Обратное утверждение также верно: если треугольник равнобедренный, то внешний угол при вершине, противолежащей основанию треугольника, в два раза больше угла при основании.
3. Решить задачу № 234 на доске и в тетрадях (рассмотреть два случая).
IV. Итоги урока.
Домашнее задание:



































