Внеурочная деятельность в 5 классе "Основы геометрии"

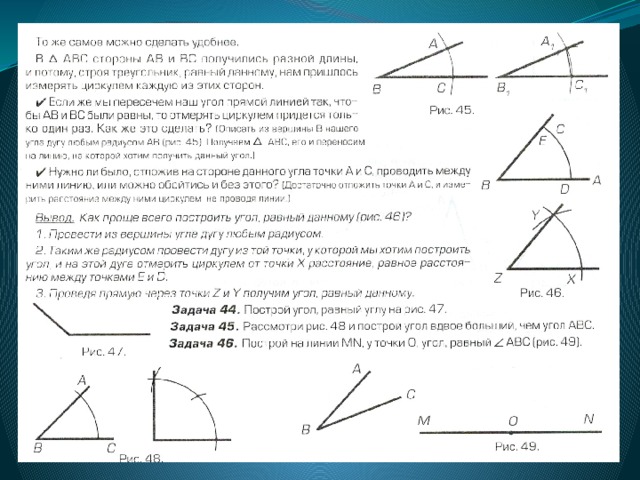
I. Что такое геометрия?

Можно ли, не взбираясь на крышу, измерить высоту дома? Можно ли, измерить поле и разделить его на несколько равных частей? Можно ли, высчитать, сколько воды содержится в каком-нибудь озере? Всему этому и всяким другим измерениям: длины, высоты, площади, объема учит нас геометрия.

Гео – земля, метрео – мерить.

Геометрия - перевод с греческого землемерие.

II. Линии

А В Что здесь нарисовано?

В Что это такое? Такая ли

А С эта линия, как первая?

Чем она отличается от первой? Какая разница между прямой линией и кривой? Как я веду карандаш, когда рисую прямую линию? Как я веду карандаш, когда рисую кривую линию?

Что это такое?

Чем отличается ломаная линия от

В прямой? Чем отличается ломаная

D от кривой?

А

C

Вывод. Ломаная состоит из нескольких отрезков прямых, а кривая на всем своем протяжении кривая.

Линии обозначают латинскими буквами. Если линия прямая, то ставят две буквы, для обозначения ломаных буквы ставят и по краям, и у каждого излома, кривые обозначают тремя буквами. Почему для обозначения прямой линии достаточно двух букв, а для прямых и ломаных недостаточно?

Задача 1. Из каких линий состоят буквы А, М, С, В?

Задача 2. Даны две точки А и В. Сколько прямых линий можно провести между ними? Сколько ломаных? Сколько кривых? Какая из этих линий самая короткая? Чем же отличается прямая линия от кривых и ломаных?

Если между двумя точками проведены прямая и несколько кривых, то та кривая, которая ближе всех к прямой, будет длинней или короче остальных?

Вывод: Чем больше кривая отходит от прямой, тем она длиннее.

Часть прямой линии, ограниченная двумя точками, называется отрезком.

Как провести отрезок такой же длины, как отрезок АВ?

Тебе поможет циркуль:

вколи слегка одну ножку циркуля в точку А и раздвинь его

настолько, чтобы острие второй ножки попало в точку В,

сними циркуль осторожно, не изменяя расстояния между

ножками, с отрезка АВ,

наложи его на какую-нибудь другую линию, на которой ты

желаешь отложить данную длину АВ.

Задача 3. Построй отрезок, равный отрезку АВ.

Задача 4. Отложи отрезок в 2 раза длиннее АВ.

Задача 5. Сложи вместе два отрезка АВ и СD.

Задача 6. Найди, на сколько отрезок АВ длиннее CD. Начерти отрезок, равный разнице длин АВ и СD.

На географических картах, планах, чертежах и т.д. предметы изображают, конечно не в своем настоящем виде, а в уменьшенном, т.е. уславливаются, что отрезок АВ какой-нибудь длины должен изображать на самом деле не эту длину, а метры и километры.

Для того, чтобы знать, какую именно длину изображает каждый отрезок чертежа, пользуются масштабом: это линия с делениями, на которых отмечены те размеры, которые изображаются ее отрезками. Если, например, мы рисуем по масштабу, то всякий отрезок, имеющий длину, равную АВ, будет равен одному метру, всякий отрезок, равный АС, - двум метрам и т.д.

Задача 7. Узнай длины отрезков Аа, Аb, Ac.

Одинаково ли расположены обе пары линий по отношению друг к другу? Чем они отличаются одна от другой? Что случится, если мы продолжим обе линии первой пары влево? Пересекутся ли также при продолжении их обе линии второй пары?

Почему ты думаешь, что линии первой пары пересекуться, а второй нет?

Потому что линии первой пары идут в разных направлениях и приближаются справа налево друг к другу. Линии второй пары идут в одном направлении, не сближаясь. Такие линии называются параллельными. (Например, рельсы.)

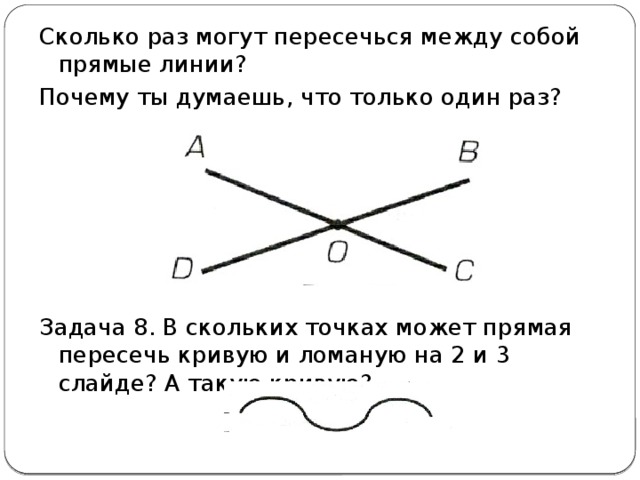
Сколько раз могут пересечься между собой прямые линии?

Почему ты думаешь, что только один раз?

Задача 8. В скольких точках может прямая пересечь кривую и ломаную на 2 и 3 слайде? А такую кривую?

III. Углы Когда две прямы встречаются в одной точке, говорят, что они образуют между собой угол. Точка, из которой они расходятся, называется вершиной угла, а сами линии (лучи) – сторонами угла.

Обозначают угол тремя буквами, причем та буква, которая обозначает вершину угла, становится посередине.

На рисунке угол АВС.

Покажи углы на тетради,

столе и т.д.

Чем больше обе линии расходятся, тем угол больше.

Задача 9. Установи между ножками циркуля некоторое расстояние. Увеличь это расстояние. Что стало с углом?

Отрежь от листа бумаги один угол и наложи его на какой-нибудь из остальных углов. Что у тебя получилось?

Когда два угла совпадают между собой, то говорят, что они равны.

Для того, чтобы два угла были равны друг другу, не нужно, чтобы стороны их были одинаковой длины, а только, чтобы стороны того и другого угла одинаково расходились между собой.

Равны ли углы на рис13?

Какой из углов больше на

рис14?

Посмотри пересекающиеся прямые.

Сколько углов образуют между

собой пересекающиеся прямые?

Назови их.

Из четырех углов, получившихся при пересечении двух прямых, те, которые расположены друг напротив друга называются вертикальными.

Задача 10. Напиши вертикальные углы на рисунке.

Какой из вертикальных углов АОВ или COD больше?

Почему ты так думаешь?

Есть здесь равные и не равные углы?

Вертикальные углы равны.

Чем отличается четверка углов на рисунках?

Если при пересечении прямых все четыре угла равны между собой, то такие углы называются прямыми.

Угол больше прямого называется тупым, угол меньше прямого – острым.

Задача 11. Какие углы (острые,

прямые, тупые) изображены на

рисунке?

Задача 12. Какие углы составляют линии, рисующие буквы А, Н?

Мы видели, что две прямы линии могут встретиться в одной точке. Можно рассмотреть еще другой случай расположения прямых линий. Получаются два угла. Такие углы

называются смежными.

Задача 13. Назови смежные углы

на рисунках.

Задача 14. Образуют ли смежные углы линии, рисующие буквы А, Х, К? Найди и назови смежные и вертикальные углы.

Задача 15. Как нужно изменить чертеж,

чтобы у угла АВС появился смежный

угол?

Задача 16. Какой угол (острый, прямой или тупой) смежен с острым (тупым, прямым) углом?

Значит, прямой угол можно определить еще так: это такой угол, который равен своему смежному.

Оказывается, углы, как и числа, можно складывать и вычитать.

Если мы раздвинем циркуль на угол АВС, а затем дальше на угол CBD? То это все равно, как если бы мы сразу раздвинули на угол… (выполни чертеж)

Если же мы сначала раздвинем циркуль на угол ABD, а затем сдвинем обратно на угол АВС, то получим угол… (выполни чертеж)

Задача 17. На сколько угол ВАС меньше прямого угла? (чертеж)

Задача 18. На сколько угол BAD больше прямого угла?

Скольким прямым углам равна сумма двух смежных углов?

Когда мы говорим, что длина нашей комнаты 7 м, что это значит?

Когда мы говорим, что какой-нибудь предмет весит

5 граммов, что это значит?

Таким образом, при измерении длины мы сравниваем ее с единицей длины; при измерении веса сравниваем его с единицей веса.

Если мы хотим измерить угол, то с чем мы его должны сравнивать? С единицей угла.

За единицу угла принимают угол, который в 90 раз меньше прямого угла, и называют его градусом.

Задача 19. Во сколько градусов углы получатся, если мы прямой угол разделим пополам?

Задача 20. Во сколько раз угол в 10 градусов меньше прямого?

III. Круг, окружность.

Воткни слегка одну ножку циркуля в бумагу и обведи вторую с карандашом вокруг первой. Что получилось?

Вся полученная фигура называется кругом, а линия, образующая круг, - окружностью.

Соедини точку (назвать точку О), в которую была воткнута ножка циркуля, с несколькими точками (A, B, C, D) окружности. При помощи циркуля определи, какая из линий ОA, ОB, ОC, ОD – короче или длиннее других? На каком расстоянии от точки О находится любая другая точка окружности?

Все точки окружности находятся на одинаковом расстоянии от точки в центре круга (ЦЕНТРА круга). Отрезки, которые соединяют центр с точками окружности называются РАДИУСАМИ. Часть круга, заключенная между двумя радиусами, называется СЕКТОРОМ круга.

Задача 21. Нарисуй на бумаге круг, вырежи его и сложи пополам. Через какую точку круга проходит линия сгиба?

Задача 22. Нарисуй круг и раздели его пополам, не вырезая и не складывая.

Что получилось бы, если бы ты провел через центр другую линию?

Всякая прямая, проходящая через центр круга, делит е его, и окружность пополам. Отрезок, который соединяет две точки окружности так, что проходит при этом через ее центр, называется ДИАМЕТРОМ.

Задача 23. Во сколько раз диаметр круга больше, чем его радиус?

Проведем из какой-нибудь точки на окружности диаметр и несколько других отрезков: АС, АD, АЕ. Какой из этих отрезков самый длинный? Какой самый короткий?

Отрезок, который соединяет какие-нибудь две точки окружности, называется хордой.

На рисунке в круге проведено несколько хорд, параллельных друг другу и диаметру (диаметр тоже хорда, раз он соединяет две точки окружности).

Какая из хорд самая длинная?

Какая самая короткая?

Вывод: Чем дальше хорда от диаметра, тем она…

Задача 24. У тебя круглая коробка радиусом 3 см. Какой длины будет самая крупная игла, которая уместится в коробке?

Задача 25. Путник идет из точки А к озеру, имеющему форму круга. В каком направле-

нии ему нужно идти, чтобы

быстрее достигнуть берега озера?

Почему? Что длинней - ОА или

ОСА? Почему? Чему равно ОС?

Задача 26. Нарисуй, как должен идти

путник, чтобы быстрее дойти до озера,

если между ним и озером находится ров

MN, через который он не может

перебраться?