Презентация "Возможности математического пакета MathCAd. Вычисления, производ-ные, интегралы. Уравнения и их системы. Символьные решения."

Возможности математического пакета MathCad. Вычисления, производные, интегралы. Уравнения и их системы. Символьные решения.

• MathCad – программное средство, среда для выполнения на компьютере разнообразных математических и технических расчетов, предоставляющая пользователю инструменты для работы с формулами, числами, графиками и текстами, снабженная простым в освоении графическим интерфейсом. В среде MathCad доступны несколько сотен операторов и логических функций, предназначенных для численного и символьного решения математических задач различной сложности. Пользователи с их помощью способны решать практически любые прикладные математические задачи.

Вычисления в MathCad

• Вычисления в MathCad проводятся через вызов оператора или вызов функции. Операторы вводятся нажатием кнопок с их изображением или комбинацией клавиш. Основные операции и способ их задания приведены в таблице 1.

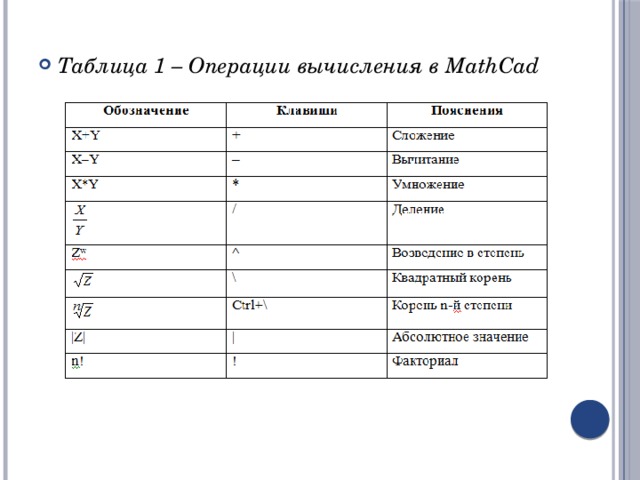
• Таблица 1 – Операции вычисления в MathCad

• Пример 2. Вычислить значение арифметического выражения:

• Решение в MathCad:

Производные в MathCad

• Оператор производной Mathcad предназначен для нахождения численного значения производной функции в заданной точке. Например, чтобы найти производную x 3  по  x  в точке x = 2, нужно выполнить следующие действия:

1. Сначала определить точку, в которой необходимо найти производную, т.е. x:=2 .

2. Ниже определения x , набрать «?» . Появляется  оператор производной с двумя полями:

3. В знаменателе набираем x – это имя переменной, по которой проводится дифференцирование:

4. Затем на поле справа от d/dx набираем x 3 – это выражение, которое нужно дифференцировать:

5. Чтобы увидеть результат, нажимаем знак «=»:

• Хотя дифференцирование возвращает только одно число, можно определить одну функцию как производную другой функции.

• Например:

• Вычисление  f ( x ) будет возвращать в численной форме производную  g ( x ) в точке  x .

• Эта методика может быть использована для вычисления производной функции в последовательности точек.

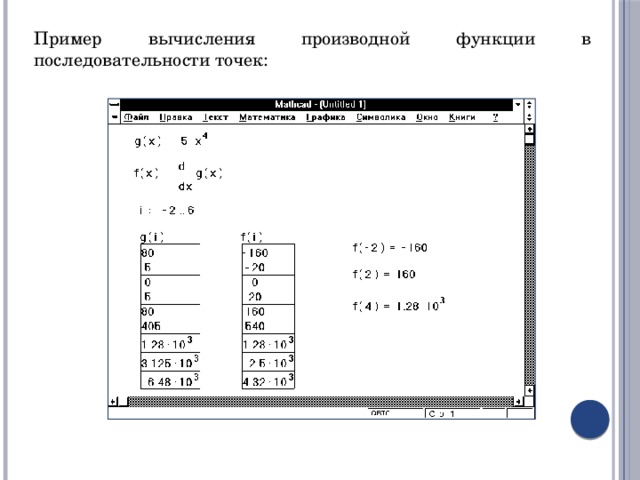
Пример вычисления производной функции в последовательности точек:

• Замечания относительно численного дифференцирования в Mathcad:

– выражение, которое нужно дифференцировать, может быть вещественным или комплексным;

– переменная дифференцирования должна быть простой неиндексированной переменной.

• В Mathcad так же существует оператор для вычисления производной  n -ного порядка. Например, чтобы найти третью производную функции x 9  по  x  в точке x = 2, нужно выполнить следующие действия:

1. Определите точку, в которой необходимо вычислить производную, т.е. x:=2.

2. Ниже определения  x , нажмите клавиши [Ctrl]?, чтобы появился    оператор  производной с двумя полями в знаменателе, одним в числителе и еще одним справа:

3. На поле внизу набираем  x – это имя переменной, по которой производится дифференцирование:

4. Далее на поле выше и правее от предыдущего и набираем 3. Это должно быть целое число между

0 и 5. Обратите внимание, что поле в числителе автоматически отображает любой порядок, печатаемый в знаменателе:

5. На поле справа от d/dx набираем x 9 – это выражение, которое нужно дифференцировать.

6. Нажимаем знак « = », чтобы получить третью производную выражения в заданной точке.

Интегралы в MathCad

• Оператор интегрирования в Mathcad предназначен для численного вычисления определенного интеграла функции по некоторому интервалу. Например, определенный интеграл sin( x ) 2  от 0 до p/4 может быть вычислен следующим образом:

1. Наберите в свободном месте знак «&», чтобы появится знак интеграла  с пустыми полями для подинтегрального  выражения, пределов  интегрирования и переменной  интегрирования:

2. Внизу набираем 0, а в верхнем поле p/4. Так задаются верхний и нижний пределы интегрирования:

3. Затем добавляем выражение, которое нужно интегрировать, т.е. sin( x ) 2 :

4. Затем набираем переменную интегрирования, т.е. x , и нажимаем знак «=» для получения результата:

• Замечания относительно численного интегрирования в Mathcad:

– пределы интегрирования должны быть вещественными. Выражение, которое нужно интегрировать, может быть, однако, вещественным либо комплексным;

– кроме переменной интегрирования, все переменные в подинтегральном выражении должны быть определены ранее в другом месте рабочего документа;

– переменная интегрирования должна быть простой переменной без индекса;

– если  переменная  интегрирования  является размерной величиной, верхний и нижний пределы интегрирования должны иметь ту же самую размерность.

• Пример вычисления интеграла с переменным пределом:

Уравнения и их системы в MathCad

• Существует два способа решения уравнений в MathCad.
• Способ №1:  использование вычислительного блока «Given – Find».
• В рабочем поле записываем первое слово «Given». Это служебное слово. Оно "подключает" определенные программные модули MathCad, необходимые для решения уравнения. Далее пишется наше уравнение в любом – явном или неявном виде. Само уравнение набирается с клавиатуры с использованием логического символа "равно". На панели Boolean он выделен жирным шрифтом.

• Далее пишется слово Find(x) (где х - переменная). Это функция, которая и получает ответ. Функцию Find(x) можно присвоить какой-либо переменной и использовать далее в расчетах. Для получения результата, после Find(x) следует поставить символ "→" либо "=«.

• Способ №2:  Применение метода «solve».
• Этот метод по существу не отличается от выше рассмотренного, поскольку процедура нахождения корня аналогична. Разница лишь в оформлении. В этом случае наше уравнение записывается без операторов Given и Find. После ввода уравнения на панели Symbolic нажимаем кнопку «solve» , определяем через запятую искомую переменную, жмем "→" и получаем ответ.

Решение системы линейных уравнений в MathCad

• Для решения системы линейных уравнений так же может использоваться блок given …find() или специальная функция lsolve(). Применение блока given …find() предопределяет необходимость задания начальных значений искомых переменных. Далее после ключевого слова given описывается СЛАУ и с помощью find() находится решение. Следует указать, что в том случае, когда СЛАУ в Mathcad имеет бесконечное множество решений блок given …find() дает конкретный результат, что несомненно следует отнести к недостаткам.

• Применение функции lsolve( ) позволяет избежать этого недостатка. Функция lsolve(M,b) имеет два аргумента. M – матрица коэффициентов при неизвестных, b – вектор свободных членов. На листинге приведен пример решения СЛАУ.

• Решение СЛАУ в MathCad:

Решение системы нелинейных уравнений в MathCad

• Для решения системы нелинейных уравнений используются два блока: given…find() и given…minerr (). Так как система нелинейных уравнений может иметь несколько решений, то полученные результаты зависят от начальных значений искомых переменных. В обоих случаях получаются приближенные решения, для которых рекомендуется делать проверку. Обычно в Mathcad требуется, чтобы количество уравнений было равно количеству искомых переменных, но в некоторых случаях, когда с точки зрения классической математики может быть получено точное решение и при меньшем количестве уравнений, данное условие может быть нарушено.

• Решение систем нелинейных уравнений в MathCad:

Символьные вычисления в MathCad

• Для выполнения символьных расчетов в MathCAD используется меню символьных вычислений "Symbolics" или палитра "Символьные вычисления".

• Основным в данной палитре является оператор "Символический знак равенства". Если при помощи него вместе знака "=" в выражениях использовать символ "→", то MathCAD будет производить аналитические вычисления вместо численных. К таким операциям относятся, например, нахождение сумм рядов, производных, определенных и неопределенных интегралов, пределов функций.

• Замечание: Если система не может выполнить символьное вычисление, то в качестве результата в этом случае выдается исходное выражение!

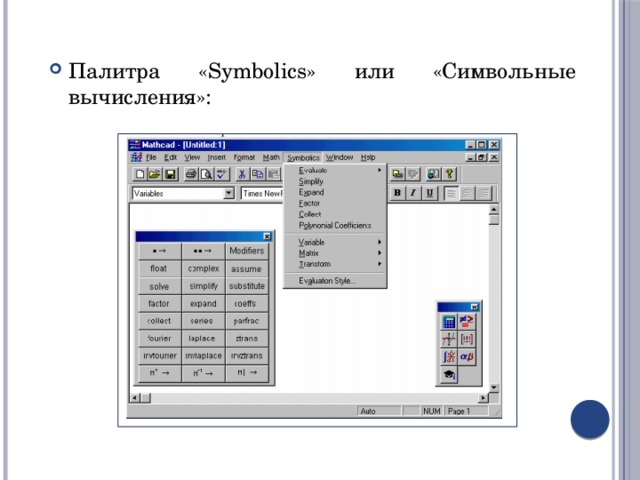
• Палитра «Symbolics» или «Символьные вычисления»:

• Примеры символьных вычислений:

Операторы палитры «Символьные вычисления»:

• simplify – упростить выражение, например:

• expand – разложить по степеням какой-либо переменной, раскрыть выражение, например:

• factor – разложить выражение на множители (операция, обратная expand), например:

• coeffs – нахождение полиномиальных коэффициентов. Эта операция аналогична команде expand с той лишь разницей, что она возвращает коэффициенты результирующего полинома в виде вектора.
• substitute – замена переменной в выражении (подстановка).
• series – разложить функцию в ряд Тейлора по указанной переменной, например:

В данном примере второй параметр, равный 4,

определяет количество членов ряда, оставляемых

при разложении.

• parfrac – разложить выражение на простые дроби, например:

• solve – решить уравнение или неравенство относительно указанной переменной. Пусть, например, необходимо решить уравнение . Для этого в MathCAD введем следующую формулу:

Заключение

• MathCAD – это мощная и в то же время простая универсальная среда для решения задач в различных отраслях науки и техники, финансов и экономики, физики и астрономии, математики и статистики.

• MathCAD остается единственной системой, в которой описание решения математических задач задается с помощью привычных математических формул и знаков.

• MathCAD позволяет выполнять как численные, так и аналитические (символьные) вычисления, при этом точность, с которой отображается результат, задается пользователем, имеет чрезвычайно удобный математико-ориентированный интерфейс и прекрасные средства научной графики.