Возрастание и убывание функции

Возрастание и

убывание

функций

Слушаю – забываю.

Смотрю – запоминаю.

Делаю – понимаю.

Конфуций

0 при х 0 f ‘ (x) 0 при 0 2) f ‘ (x) = 0 при х=0 6) f ‘ (x) = 0 при х=3 f ‘ (x) f ‘ (x) 0 при х 0 f ‘ (x) 0 при х 3 3) Решений нет 4) f ‘ (x) 0 при х -½ " width="640"

Проверка домашнего задания

№ 883

• f ‘ (x) = 0 при х=0 5) f ‘ (x) = 0 при х=16

f ‘ (x) 16

f ‘ (x) 0 при х 0 f ‘ (x) 0 при 0

2) f ‘ (x) = 0 при х=0 6) f ‘ (x) = 0 при х=3

f ‘ (x)

f ‘ (x) 0 при х 0 f ‘ (x) 0 при х 3

3) Решений нет

4) f ‘ (x) 0 при х -½

Составь пару

Работаем самостоятельно

1

х

2

6

2х

3

7

11

-3

1

a

Sin х

4

8

12

16

- sinx

2

cosx

17

13

5

9

10

18

14

0

ax

19

15

20

Ответ.

Составь пару

1 -9

5 -19

2 -4

6 -10

3 -5

10 -20

4 -19

7 -18

11 -14

16 -19

17 -13

8 -17

12 -19

15 -16

Изучение нового материала

• Признак возрастания функции
• Признак убывания функции
• Как определить промежутки убывания и возрастания функции

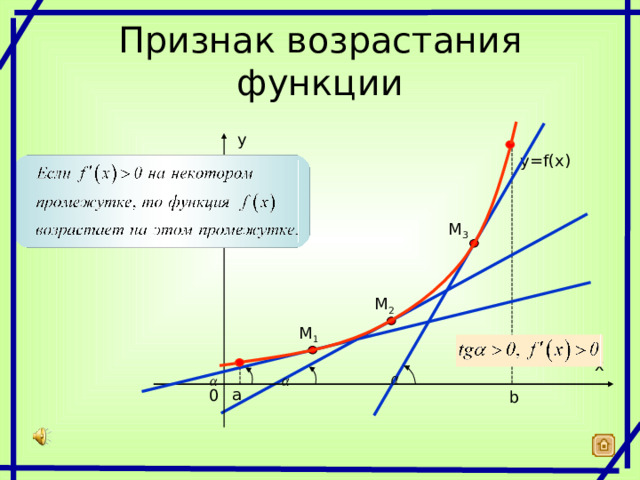
Признак возрастания функции

y

y = f(x)

M 3

M 2

M 1

x

а

0

b

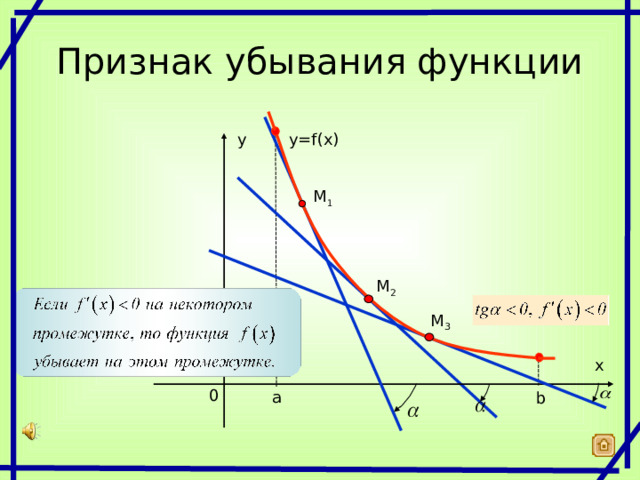
Признак убывания функции

y = f(x)

y

M 1

M 2

M 3

x

0

а

b

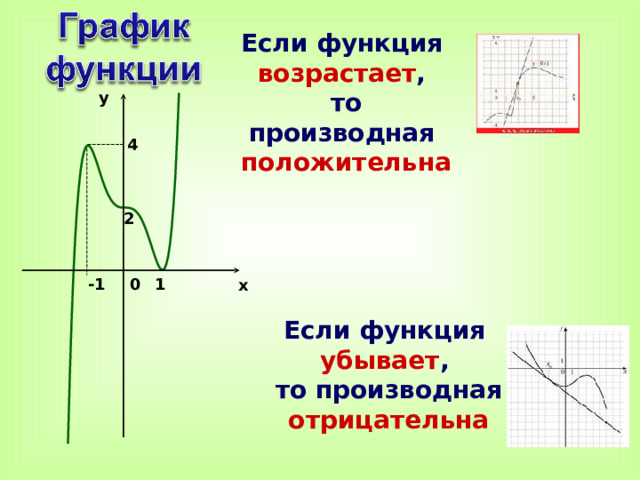
Если функция возрастает ,

то производная

положительна

y

4

2

-1

0

1

x

Если функция убывает ,

то производная

отрицательна

Как определить промежутки убывания и возрастания функции

Алгоритм:

Пример 1

Пример 2

Как определить промежутки убывания и возрастания функции

Посмотреть график

функции

Х

+

-

-

2

-1

Алгоритм

График функции

Х

График функции

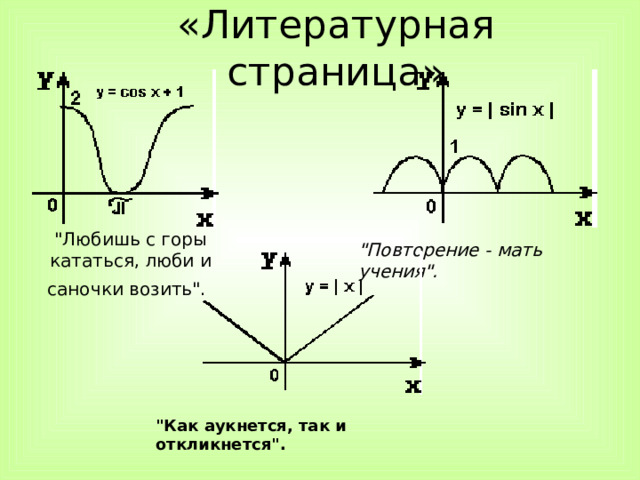
Пословицы и графики функций

Первая женщина математик

С. В. Ковалевская сказала:

« Математик  должен быть поэтом в душе».

Подберите к графикам функций, изображенных на слайдах, пословицы, которые раскрывают суть процессов функции

"Как аукнется, так и откликнется".

«Литературная страница»

"Любишь с горы кататься, люби и саночки возить".

"Повторение - мать учения".

Учащиеся работают в парах, решение записывают в тетрадях.

а) у = х³ — 6 х² + 9 х — 9;

б) у = 3 х² — 5х + 4.

Один работает у доски.

а) у = 2 х³ – 3 х² – 36 х + 40

б) у = 4 х - 2 х³

• То, что мы знаем, - ограниченно, а то, что не знаем, - бесконечно.

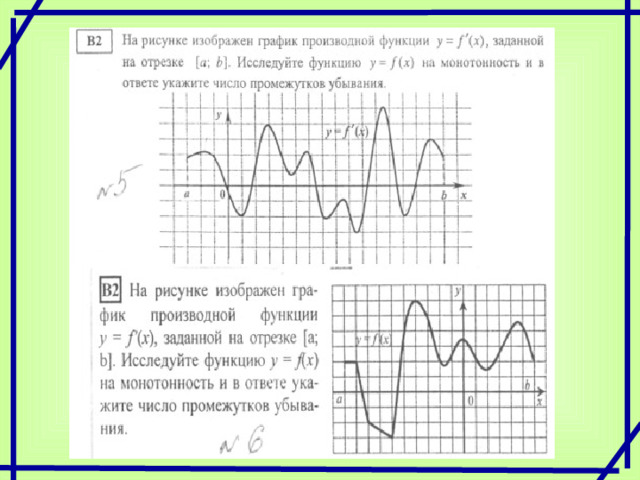
Функция у = f ( x ) определена на отрезке [-6; 6]. На рисунке 104 изображен ее график. Укажите число промежутков, на которых отрицательна функция у = f '(х).

3

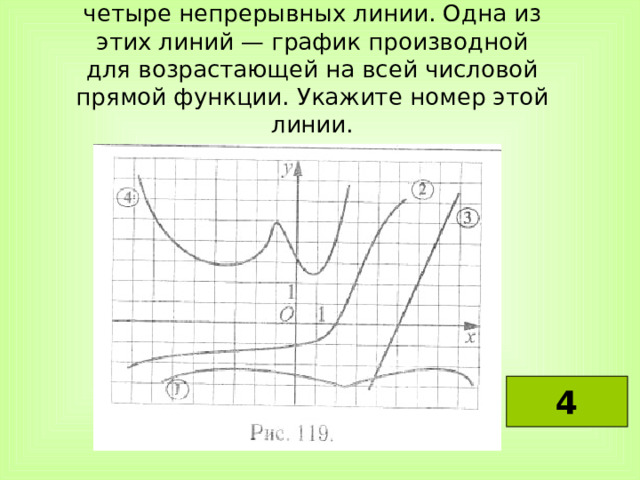
На рисунке 119 изображены четыре непрерывных линии. Одна из этих линий — график производной для возрастающей на всей числовой прямой функции. Укажите номер этой линии.

4

0 2 в каждой точке интервала I , то функция возрастает на I . 2 Достаточный признак убывания функции 3 Если f′(х) в каждой точке интервала I , то функция убывает на I . . 3 геометрический смысл производной 4 Физический смысл производной функции Скорость изменения функции 4 " width="640"

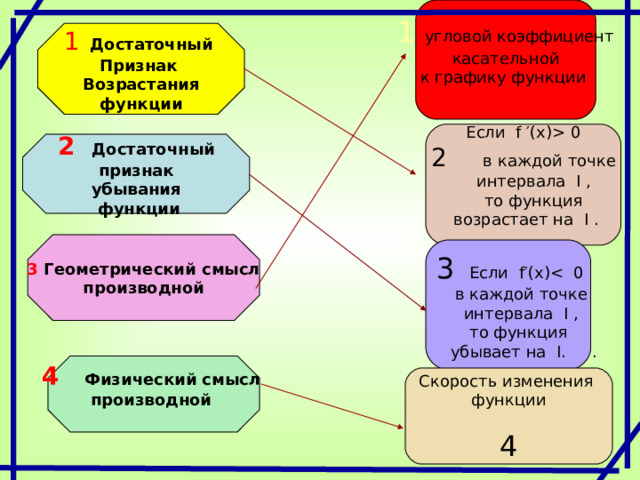
1 угловой коэффициент касательной

к графику функции

1 Достаточный

Признак

Возрастания

функции

Если f ′(х) 0

2 в каждой точке

интервала I ,

то функция

возрастает на I .

2 Достаточный

признак

убывания

функции

3 Если f′(х)

в каждой точке

интервала I ,

то функция

убывает на I . .

3 геометрический смысл

производной

4 Физический смысл

производной

функции

Скорость изменения функции

4

0 2 в каждой точке интервала I , то функция возрастает на I . 2 Достаточный признак убывания функции 3 Геометрический смысл производной 3 Если f′(х) в каждой точке интервала I , то функция убывает на I . . 4 Физический смысл производной Скорость изменения функции 4 " width="640"

1 угловой коэффициент

касательной

к графику функции

1 Достаточный

Признак

Возрастания

функции

Если f ′(х) 0

2 в каждой точке

интервала I ,

то функция

возрастает на I .

2 Достаточный

признак

убывания

функции

3 Геометрический смысл

производной

3 Если f′(х)

в каждой точке

интервала I ,

то функция

убывает на I . .

4 Физический смысл

производной

Скорость изменения

функции

4

Ну кто придумал эту математику !

У меня всё получилось!!!

Надо решить ещё пару примеров.

Перевод баллов в оценку

29 баллов и более – оценка «5»

20 – 28 баллов – оценка «4»

9 – 19 баллов – оценка «3»

0 – 8 баллов – оценка «2»

• я уверен __________________________
• я затрудняюсь _________________________
• я научился ____________________________
• урок дал мне для жизни ___________________

§ 49

№ 900(1,3,5), 902 (1,2)

№ 901*

К высотам познанья!

За кручей обрыв!

Дороги орлам незнакомы.

Пройдет человек лишь,

Но прежде открыв

Природы и чисел законы.

Искателей истин судьба нелегка,

Но тень их достанет в веках облака