Возрастание и убывание функции

Урок № 39

Тема: Признак возрастания и убывания функции

Цели урока:

• ввести признак возрастания, убывания функции и показать его применение при решении заданий;

• развить познавательную активность, интерес к предмету;

• воспитать точность, логичность в мышлении.

Ход урока:

1. Организационный момент

Сообщение темы урока и его целей

1. Текущее повторение

Ученики выполняют задания. Ответы проверяются с помощью таблицы.

Задания: найдите y'(x) или y'(x₀).

I вариант II вариант

1. y = 5x² + 4, x₀ = 6 1. y = 0,5x² – 6x + 1/5

2. y = 15cosx + 3 2. y = 11 + 8sinx

3. y = -0,5x² + 6x + 17 3. y = 2√x + 4x, x₀ = 9

4. y = 1/x + 2√x 4. y = 4/x – √x

5. y = 2x + cosx 5. y = 7,9 + 2x², x₀ = 0

6. y = 60x + 4,8 6. y = sinx – cosx

7. y = 3,5x² – 12, x₀ = 1/7 7. y = cosx + 2sinx

Ответы:

1. 60 1. 1 -6х

2. -15 sinx 2. 8соsх

3. х +6 3. 4/3

4. -1/х² + 1/√х 4. -4/х² – 1/(2√х)

5. 2 – sinх 5. 0

6. 60 6. Cosx + sinx

7. 1 7. – sinх +2 cosx

8. Решить неравенство методом интервалов: х⁴ – 4х² 0.

9. Указать промежутки возрастания, убывания функций:

у = 2/х; у = х² – 4; у = -х² + 3х +6; у = 0,2х⁵ – 4/3 х³

Выполнив первые три задания, получаем проблему: как найти промежутки монотонности для четвертой функции?

1. Введение нового материала (в ходе фронтальной беседы с элементами исследования).

1. Какая функция называется возрастающей, убывающей?

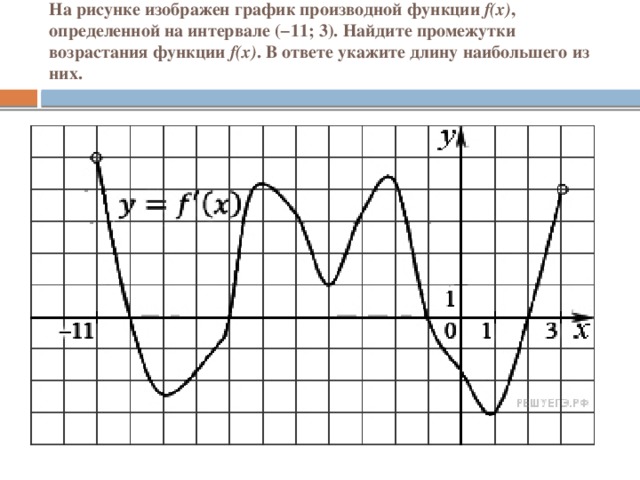
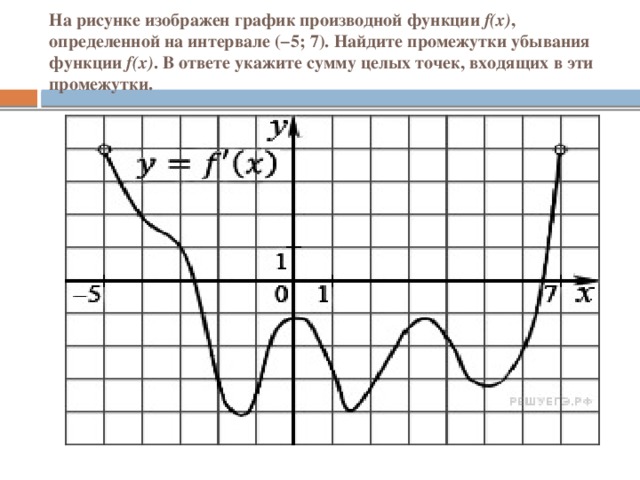
2. Для функций, графики которых изображены на рисунках, укажите промежутки возрастания, убывания (на рисунках графики различных функций).

Разбор второго индивидуального задания.

1. Как определить промежутки возрастания, убывания функции

у = 0,2х⁵ – 4/3 х³

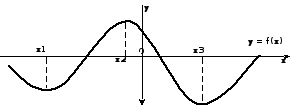
Для этого исследуем график некоторой функции (предложен на рисунке).

На каждом из промежутков (-∞;х₁), (х₁;х₂), (х₂;х₃), (х₃;+∞) построим касательные.

α₂

Задание. Проанализировать расположение касательных по отношению к оси абсцисс (угол наклона) и определить знаки значений производной.

Учащиеся самостоятельно делают вывод.

Вывод:

1. Достаточный признак возрастания функции. Если f '(x) 0 в каждой точке интервала У, то функция f возрастает на У.

2. Достаточный признак убывания функции. Если f '(x) f убывает на У.

Учащиеся вместе с учителем составляют план исследования функции на возрастание (убывание).

План:

1. Найти область определения.

2. Найти производную функции.

3. Найти точки, в которых производная равна нулю или не существует.

4. Определить знаки производной.

5. Вывод о «поведении» функции.

Пример.

у = 0,2х⁵ – 4/3 х³

1. определена при любом х

2. у ' = х⁴ – 4х²

3. у ' существует во всех точках.

у ' = 0; х⁴ – 4х² = 0;

х²(х – 2)(х + 2) = 0

у ' + – – + х

у

1. Функция возрастает на луче (–∞; –2] и на луче [2; +∞).

Функция убывает на отрезке [–2; +2].

1. Закрепление материала.

Учащиеся выполняют задания по порядку (каждый в своем темпе), учитель проверяет, дает рекомендации каждому индивидуально.

№280 (б, г), №283 (а, б)

1. Итог урока и д/з : №281(а,б) , № 284 (а,в)

1 3 ноября.

Классная работа.

Возрастание и убывание функции.

Возрастание и убывание функции

Иду под гору. Функция убывает на промежутке [a ;с ]

Иду в гору. Функция возрастает на промежутке [b ; a]

y

a

b

c

x

Найдите производную функции:

• f(x)=3x ³-2x²-3x+5
• f(x)=2x²+4x-4
• f(x)=sinx
• f(x)=sin2x
• f(x)=√x
• f(x)=2cosx
• f(x)=cosx+10

0, то f(x) – возрастает б) f ´(x) в) f ´(x) = 0, то f(x) – постоянна(константа)" width="640"

Теорема: f(x) – непрерывна на I и имеет f ´(x)

а) f ´(x) 0, то f(x) – возрастает

б) f ´(x)

в) f ´(x) = 0, то f(x) – постоянна(константа)

0, x ϵ (-∞; 1 ) и (3; + ∞ ) f ´(x)

f(x) = x³ - 6x² + 9x – 1

f ´(x) = 3x² - 12x + 9

Найдем критические точки:

f ´(x) = 0, 3x² - 12x + 9 = 0

x² - 4x + 3 = 0

x = 1 и х = 3

f ´(x)

+

-

+

х

1

3

f(x)

max

min

f ´(x) 0, x ϵ (-∞; 1 ) и (3; + ∞ )

f ´(x)

• №№ 5.51 (а,б)
• 5.58 (а)

• №№ 5.58 (б),
• 5.57 (а-в)

На рисунке изображён график  производной функции  и восемь точек на оси абсцисс. В скольких из этих точек функция  убывает?

На рисунке изображён график ( x ) производной функции  f ( x ) и восемь точек на оси абсцисс:  x 1 ,  x 2 ,  x 3 , ...,  x 8 . В скольких из этих точек функция  f ( x ) возрастает?

  На рисунке изображен график производной функции  f(x) , определенной на интервале (−2; 12). Найдите промежутки убывания функции  f(x) . В ответе укажите длину наибольшего из них.

На рисунке изображен график производной функции  f(x) , определенной на интервале (−11; 3). Найдите промежутки возрастания функции  f(x) . В ответе укажите длину наибольшего из них.

На рисунке изображен график производной функции  f(x) , определенной на интервале (−5; 7). Найдите промежутки убывания функции  f(x) . В ответе укажите сумму целых точек, входящих в эти промежутки.