| Тема | Цели | Задачи | Контрольные вопросы и задания | Д/з |
| Возведение комплексного числа в степень. | Дидактическая
| Обобщить и систематизировать ЗУН студентов по представлению комплексного числа в тригонометрической и показательной формах, изучить формулу возведения комплексного числа в степень, начать формирование умений и навыков возведения комплексного числа в степень. | 1) Обобщить и систематизировать ЗУН студентов по представлению комплексного числа в тригонометрической и показательной формах. 2) Изучить формулу возведения комплексного числа в степень. 3) Начать формирование умений и навыков возведения комплексного числа в степень.. | Контрольные вопросы и задания занятия | Изучить и записать конспект лекции, вычислить 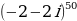 . . |
| Развивающая
| Развивать логическое мышление и память. |
| Воспитательная | Воспитывать любознательность и самостоятельность. |
Возведение комплексного числа в степень.
1) Закрепление знаний, умений и навыков представления комплексного числа в тригонометрической и показательной формах (ответить на вопросы, решить задания и записать в конспект).
ВОПРОСЫ И ЗАДАНИЯ:
1) Сколько форм имеет комплексное число?
2) Назовите формы комплексного числа.
3) Какое комплексное число не может иметь тригонометрической и показательной формы? Почему?
4) В какой форме комплексные числа удобно складывать, вычитать, умножать и делить?
5) Какие основные понятия комплексного числа используются для представления его в тригонометрической и показательной формах?
2) Мотивация изучения нового материала (ознакомиться).
Для полного освоения теории комплексных чисел нам необходимо научиться выполнять с комплексными числами ещё две операции: возводить в степень и извлекать из под корня.
Почему эти операции нерационально выполнять в алгебраической форме?
Как их выполнять?
Всё это мы узнаем на сегодняшнем занятии.
3) Актуализация опорных знаний (изучить и записать в конспект).
Для изучения темы "Возведение комплексного числа в степень" нам необходимо ещё раз повторить как комплексное число представить в тригонометрической и показательной степени. Особенно - тригонометрической.
Пример 1. Представьте комплексное число 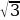 - і в тригонометрической и показательной формах.
- і в тригонометрической и показательной формах.
Решение.
Для того, чтобы выполнить данное задание по формуле (1) нам необходимо найти модуль r и аргумент φ данного числа, а затем применить формулу (1).
Проанализируем условие:
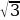 - і, a =
- і, a =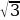 , b = -1, IV четверть.
, b = -1, IV четверть.
Сначала найдем модуль r:
r = |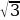 - і | =
- і | =  =
= 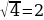 .
.
Теперь по алгоритму найдем аргумент φ (мы уже его находили):
1) α = arctg | 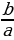 | = arctg |
| = arctg | 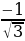 | = arctg
| = arctg 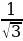 =
= 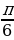
2) φ = (формула для четвёртой четверти) = 2π- α = 2π- 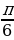 =
= 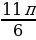 .
.
Теперь запишем формулу, подставляя найденные значения:
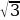 - і = 2 ∙ (
- і = 2 ∙ (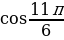 + і ∙
+ і ∙ 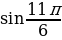 ) =
) =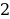 ∙
∙ 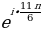 . Ничего упрощать не надо.
. Ничего упрощать не надо.
Пример 2. Представьте комплексное число -1 + 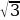 і в тригонометрической и показательной формах. Решить самостоятельно.
і в тригонометрической и показательной формах. Решить самостоятельно.
Пример 3. Представьте комплексное число 5 в тригонометрической и показательной формах.
Решение.
Заданное комплексное число 5 имеет неполную форму (a = 5, b = 0), четверть не определяется (число находится на границе четверти, т.е. на какой-то оси). Поэтому модуль r и аргумент φ данного числа находить проще, чем полного комплексного числа:
r = |5 | = (это просто модуль числа 5) = 5.
Аргумент φ комплексного числа 5 найдём на основании определения аргумента, учитывая, что геометрическое изображение (точка) для данного числа находиться на положительной части оси ОХ. Тогда угол между положительным направлением ОХ и отрезком ОМ (М - геометричексое изображение комплексного числа) равен 0, т.е.
φ = 0.
Теперь запишем формулу, подставляя найденные значения модуля r и аргумента φ в формулу а + bі = r ∙ (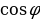 + і ∙
+ і ∙ 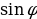 ) = r ∙
) = r ∙ 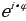 (1)
(1)
:
5 = 5 ∙ (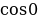 + і ∙
+ і ∙ 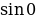 ) =
) =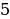 ∙
∙ 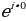 . Ничего упрощать не надо.
. Ничего упрощать не надо.
Пример 4. Представьте комплексное число 2і в тригонометрической и показательной формах. Решить самостоятельно (геометрическое место данного числа будет находиться на положительном направлении оси ОУ, φ = 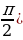 .
.
4) Изучение нового материала. Возведение комплексного числа в степень (изучить и записать в конспект).
Сложение, вычитание, умножение и деление комплексных чисел удобно выполнять в алгебраической форме. При возведении комплексного числа в алгебраической форме в степень нам пришлось бы многократно умножать комплексное число на себя, что привело бы к трудоёмкой работе и массе технических ошибок.
Поэтому для возведения в степень лучше использовать тригонометрическую форму комплексного числа и формулу:
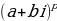 =
= 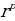 ∙ (
∙ (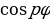 + і ∙
+ і ∙  ).
).
Пример 5. Вычислите 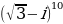 .
.
Решение.
Для возведения в степень р 3 нужно использовать формулу, записанную на предыдущем занятии:
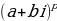 =
= 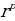 ∙ (
∙ (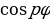 + і ∙
+ і ∙  ) (2).
) (2).
Для этого нам необходимо найти модуль r и аргумент φ данного числа. Это задание выполнено в Примере 1:
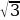 - і, a =
- і, a =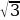 , b = -1, IV четверть.
, b = -1, IV четверть.
Сначала найдем модуль r:
r = |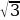 - і | =
- і | =  =
= 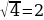 .
.
Теперь по алгоритму найдем аргумент φ (мы уже его находили):
1) α = arctg | 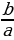 | = arctg |
| = arctg | 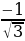 | = arctg
| = arctg 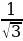 =
= 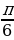
2) φ = (формула для четвёртой четверти) = 2π- α = 2π- 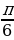 =
= 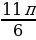 .
.
Теперь подставим всё в формулу (2), учитывая, что р = 10:
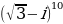 =
= 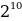 ∙ (
∙ (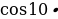
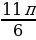 + і ∙
+ і ∙ 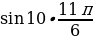 ) = (выполним несложные упрощения) = 1024 ∙ (
) = (выполним несложные упрощения) = 1024 ∙ (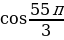 + і ∙
+ і ∙ 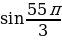 ). Ничего упрощать не надо.
). Ничего упрощать не надо.
Пример 6. Вычислите 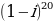 . Решить самостоятельно.
. Решить самостоятельно.
3) Изучение нового материала. Извлечение комплексного числа из под корня (изучить и записать в конспект).
Корнем n-й степени из комплексного числа z называется такое комплексное число w, n-я степень которого равна z, т.е. 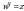 , где n - натуральное число. (Обозначение
, где n - натуральное число. (Обозначение 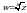 ).
).
Для любого натурального числа n и любого комплексного числа 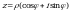 , где z 0, существует n различных значений корня n-й степени, которые находятся по формуле:
, где z 0, существует n различных значений корня n-й степени, которые находятся по формуле:
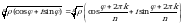 , где k=0, 1, 2…, n-1, n
, где k=0, 1, 2…, n-1, n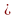 N.
N.
Пример 6. Найти все значения 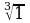 .
.
Решение.
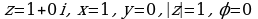 .
.
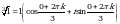 , где k = 0,1,2.
, где k = 0,1,2.
k = 0, тогда 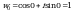 ;
;
k = 1, тогда 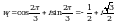 ;
;
k = 2, тогда 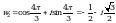 .
.
Ответ: 1; 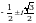 .
.
Можно доказать, что все значения 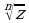 являются вершинами правильного n-угольника, вписанного в окружность радиуса
являются вершинами правильного n-угольника, вписанного в окружность радиуса 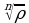 , значения аргументов соседних точек отличаются на
, значения аргументов соседних точек отличаются на 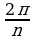 .
.
5) Домашнее задание. Изучить и записать конспект лекции, вычислить 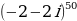 .
.







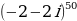 .
.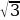 - і в тригонометрической и показательной формах.
- і в тригонометрической и показательной формах. =
= 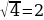 .
.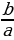 | = arctg |
| = arctg | 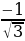 | = arctg
| = arctg 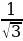 =
= 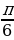
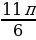 .
.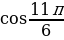 + і ∙
+ і ∙ 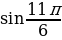 ) =
) =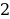 ∙
∙ 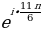 . Ничего упрощать не надо.
. Ничего упрощать не надо.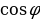 + і ∙
+ і ∙ 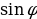 ) = r ∙
) = r ∙ 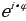 (1)
(1)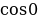 + і ∙
+ і ∙ 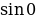 ) =
) =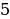 ∙
∙ 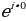 . Ничего упрощать не надо.
. Ничего упрощать не надо.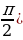 .
.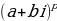 =
= 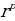 ∙ (
∙ (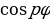 + і ∙
+ і ∙  ).
).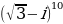 .
.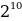 ∙ (
∙ (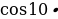
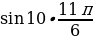 ) = (выполним несложные упрощения) = 1024 ∙ (
) = (выполним несложные упрощения) = 1024 ∙ (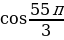 + і ∙
+ і ∙ 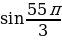 ). Ничего упрощать не надо.
). Ничего упрощать не надо.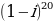 . Решить самостоятельно.
. Решить самостоятельно.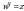 , где n - натуральное число. (Обозначение
, где n - натуральное число. (Обозначение 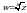 ).
).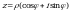 , где z 0, существует n различных значений корня n-й степени, которые находятся по формуле:
, где z 0, существует n различных значений корня n-й степени, которые находятся по формуле: 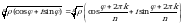 , где k=0, 1, 2…, n-1, n
, где k=0, 1, 2…, n-1, n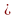 N.
N.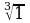 .
.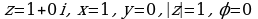 .
.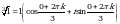 , где k = 0,1,2.
, где k = 0,1,2.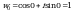 ;
;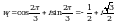 ;
;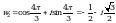 .
.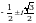 .
.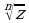 являются вершинами правильного n-угольника, вписанного в окружность радиуса
являются вершинами правильного n-угольника, вписанного в окружность радиуса 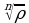 , значения аргументов соседних точек отличаются на
, значения аргументов соседних точек отличаются на 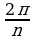 .
.



















