Вписанная окружность_урок2

Вписанная окружность

Ответ: 1

Ответ: 3 см

Ответ: 20

Ответ: 8 и 10

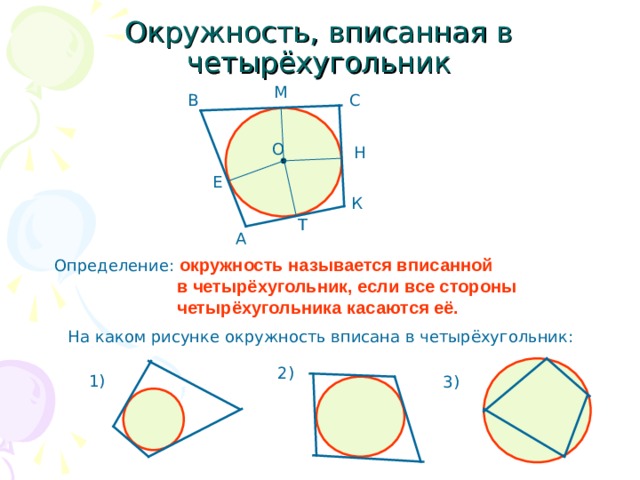
Окружность, вписанная в четырёхугольник

М

В

С

О

Н

Е

К

Т

А

Определение: окружность называется вписанной

в четырёхугольник, если все стороны

четырёхугольника касаются её.

На каком рисунке окружность вписана в четырёхугольник:

2)

1)

3)

Теорема: если в четырёхугольник вписана окружность,

то суммы противоположных сторон

четырёхугольника равны ( в любом описанном

четырёхугольнике суммы противоположных

сторон равны) .

М

В

С

О

Н

АВ + СК = ВС + АК.

Е

К

Т

А

Обратная теорема: если суммы противоположных сторон

выпуклого четырёхугольника равны,

то в него можно вписать окружность.

( доказательство – в учебнике № 724 )

Задача : в ромб, острый угол которого 60 0 , вписана окружность,

радиус которой равен 2 см. Найти периметр ромба.

В

L

S

Дано: Окр.(О; 2 см) вписана

в ромб FSLZ, F = 60 0 .

O

Найти: Р FSLZ

2

Решение:

Z

С

А

F

Т. к. окружность вписана в ромб, то стороны ромба

касаются окружности, значит, АВ FZ, AB = 2r = 4 см – диаметр.

Проведём SC FZ, SC = AB (как перпендикуляры между

параллельными прямыми), SC = 4 см

FSC – прямоугольный ,

(c м).

Р FSLZ = 4FS = 4 ·

см

Ответ:

Реши задачи

В

1)

С

Дано: Окр.(О; r ) вписана в АВСК,

Р АВСК = 10

О

Найти: ВС + АК

r

К

А

2)

В

С

6

Дано: АВСМ описан около Окр.(О; r)

BC = 6, AM = 15,

СМ = 2 АВ

Найти: АВ, СМ

А

М

15