ВПР физика 7 класс Задания 11 ключи

Задания 11. Расчетная задача

1. Задание 11 № 11

Сколько времени должен непрерывно работать насос мощностью 50 кВт, чтобы из колодца глубиной 50 м откачать воду, объёмом 100 м³? Плотность воды равна 1000 кг/м³. Ускорение свободного падения g = 10 м/с².

Пояснение.

Обозначим: P = 50 кВт, h = 50 м, V = 100 м³, ρ = 1000 кг/м³.

Время равно отношению совершаемой насосом работы к его мощности: t = A / P.

Вода объёмом V имеет массу m = ρV. Чтобы поднять такую массу на высоту h нужно совершить работу против силы тяжести F = mg, равную A = Fh.

Таким образом, t = ρVgh / P = 1000 c.

Ответ: t = 1000 c.

2. Задание 11 № 77

Из залитого подвала, площадь пола которого равна 50 м², требуется откачать воду на мостовую. Глубина воды в подвале 1 м, а расстояние от уровня воды в подвале до уровня мостовой 2 м. Определите работу, которую надо совершить, чтобы откачать воду. Плотность воды 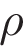 = 1000 кг/м³. Ускорение свободного падения g = 10 м/с².

Пояснение.

Обозначим: S = 50 м², h₁ = 1 м, h₂ = 2 м.

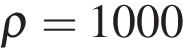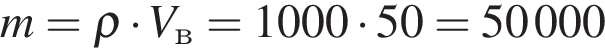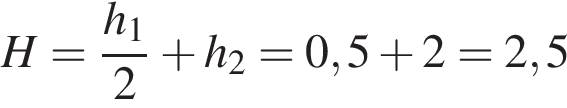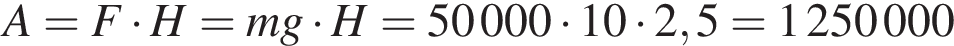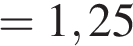Объём воды в подвале равен произведению высоты уровня воды на площадь пола:  м³. Плотность воды равняется  кг/м³. Следовательно, масса воды, которую необходимо откачать, равняется  кг. Высота подъёма от центра масс равняется  м. Следовательно, работа, которую надо совершить, чтобы откачать воду, равняется Дж  МДж.

Ответ: A = 1,25 МДж.

3. Задание 11 № 78

Найти мощность потока воды, протекающей через плотину, если высота падения воды 25 м, а расход её — 120 м³ в минуту. Плотность воды 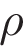 = 1000 кг/м³. Ускорение свободного паденияg = 9,8 Н/кг.

Пояснение.

Обозначим: h = 25 м, V = 120 м³, 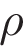 = 1000 кг/м³, t = 60 с, g = 9,8 Н/кг.

Масса падающей воды: 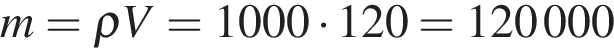 кг. Сила тяжести, действующая на воду, равняется  Н.

Работа, совершаемая потоком в минуту, равняется Дж. Мощность потока определяется по формуле 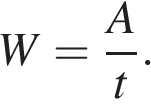 Следовательно, мощность потока равняется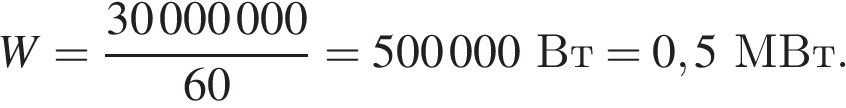 

Ответ: W = 0,5 МВт.

4. Задание 11 № 79

Из колодца глубиной 40 м поднимают ведро с водой массой 14 кг на цепи, масса каждого метра которой равна 1 кг. Какая при этом совершается работа? Ускорение свободного паденияg = 10 Н/кг.

Пояснение.

Обозначим: m_в = 14 кг, h = 40 м, 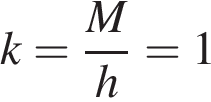 кг/м, g = 10 Н/кг.

Необходимо совершить работу по поднятию цепи и работу по поднятию ведра. Обозначим и как 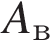 и 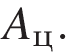 Тогда полная работа  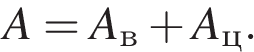Высотой ведра можно пренебречь, поэтому работа по поднятию ведра  На высоту h поднимается только самый нижний конец цепи, поэтому можно считать, что мы поднимаем центр тяжести цепи, т.е. вся масса цепи сосредоточена в точке приложения силы тяжести, находящейся в центре цепи. Эта точка поднимается на высоту 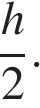 Следовательно,  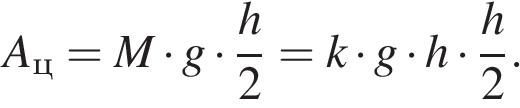Теперь можем найти полную работу:

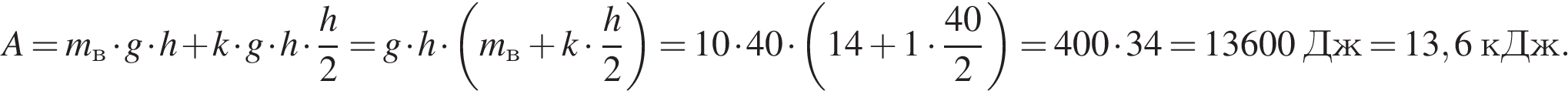
Ответ: A = 13,6 кДж.

5. Задание 11 № 83

Из воды с глубины 5 м поднимают до поверхности камень объёмом 0,6 м³. Плотность камня 2500 кг/м³. Найдите работу по подъёму камня. Плотность воды 1000 кг/м³. Ускорение свободного падения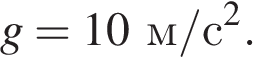 

Пояснение.

Обозначим: h = 5 м, V = 0,6 м³,  кг/м³, 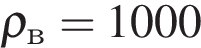 кг/м³, .

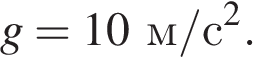Работа по подъёму камня с глубины 5 м равняется произведению высоты поднятия на ускорение свободного падения, на объём камня и разницу между плотностью камня и плотностью воды:

Ответ: A = 45 кДж.

6. Задание 11 № 85

Определите мощность двигателя, совершающего в течение часа работу 18 000 кДж.

Пояснение.

Для того, чтобы определить мощность двигателя, нужно воспользоваться формулой мощности. Переведём кДж в Дж и часы в секунды, получим:  Дж,  с. Таким образом, подставляя числовые значения в формулу, получим: 

Ответ: W = 5 кВт.

7. Задание 11 № 86

Сколько времени должен работать двигатель мощностью 25 кВт, чтобы совершить работу 36 000 кДж?

Пояснение.

Для того, чтобы определить время, которое потребуется для совершения данной работы, нужно воспользоваться формулой мощности  и выразить из неё  Таким образом, подставляя числовые значения в формулу, получим: 

Ответ: t = 0,4 ч.

8. Задание 11 № 87

Из шахты глубиной 200 м поднимают груз массой 500 кг на канате, каждый метр которого имеет массу 1,5 кг. Определите КПД установки. Ускорение свободного падения 

Пояснение.

Обозначим:  м,  кг,  кг/м, 

Общая работа складывается из работы по подъему груза и работы по подъему каната:  Работа по подъёму груза  Так как масса каната меняется линейно с его длиной от максимального значения (масса всего каната) до нуля, а в среднем — это половина максимального значения, то работа будет равна половине максимального значения, умноженного на длину каната:  Значит, общая работа:

КПД — это отношение полезной работы к затраченной. Полезной работой в данном случае является работа по подъему груза. Затраченной — работа по подъему груза и каната. Таким образом, получаем:

КПД установки равен 77%.

Ответ: 

9. Задание 11 № 90

Вычислите полезную мощность насоса, подающего ежеминутно 1300 л воды на высоту 24 м. Плотность воды  Ускорение свободного падения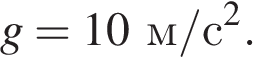 

Пояснение.

Обозначим:   м,  л, ,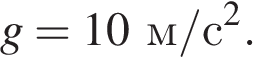 

Масса воды, которую подаёт насос ежеминутно  кг. Работа насоса равняется произведению силы на высоту, т.е. произведению массы воды на ускорение свободного падения и высоту:  Теперь воспользуемся формулой мощности 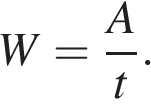 Подставляя в неё числовые значения, получаем: 

Ответ: W = 5,2 кВт.

10. Задание 11 № 92

Оконная штора массой 1,4 кг и длиной 2 м свёртывается на тонкий валик наверху окна. Какая при этом совершается работа? Трением и толщиной валика пренебречь. Ускорение свободного падения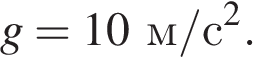 

Пояснение.

Обозначим:  кг,  м,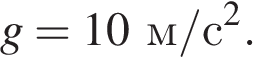 

Чтобы найти работу, которая совершается при свёртывании шторы, нужно заметить, что при свёртывании шторы её вес уменьшается. Поэтому работа равняется  Дж.

Ответ: A = 14 Дж.

11. Задание 11 № 93

Вычислите мощность, развиваемую при обработке детали на строгальном станке, если резец проходит в 1 с расстояние 56 см, а сила резания равна в среднем 3,6 кН.

Пояснение.

Обозначим: t = 1 с,  

Чтобы найти мощность, развиваемую при обработке детали, требуется сначала найти работу. Работа вычисляется по формуле  Подставим числовые значения в формулу и найдём  Дж. Теперь найдём мощность  Вт.

Ответ: W = 2016 Вт.

12. Задание 11 № 94

Наибольшая мощность, которую может развивать магистральный электровоз ВЛ-85 при непрерывной работе в течение часа, равна 11 400 кВт. Какую работу совершит такой двигатель за это время?

Пояснение.

Обозначим:  .

Чтобы найти работу, которую совершит такой двигатель за данное время, необходимо воспользоваться формулой мощности и выразить из неё работу:  Подставим числовые значения в полученную формулу и найдём работу: 

Ответ: A = 41 040 МДж.

13. Задание 11 № 95

Мощность двигателя транспортёра равна 1 кВт. За какое время он может поднять на высоту 6 м 40 м³ песка? Плотность песка 1500 кг/м³. Ускорение свободного падения g = 10 м/с².

Пояснение.

Обозначим:  h = 6 м, V = 40 м³,  g = 10 м/с².

Мощность находится по формуле 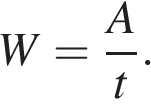 Работа находится по формуле  Силу можно найти по формуле  Чтобы найти массу, необходимо плотность умножить на объём:  Таким образом, из получившейся формулы  выразим время: 

Ответ: t = 1 ч.

14. Задание 11 № 98

Тепловоз тянет состав со скоростью 72 км/ч, развивая мощность 880 кВт. Как велика в этом случае сила тяги?

Пояснение.

Обозначим:  W = 880 кВт = 880 000 Вт.

Из формулы мощность  выразим :  Таким образом, подставляя числовые значения в формулу, вычислим 

Ответ: F = 44 кН.

15. Задание 11 № 99

Пузырёк метана объёмом 2 см³, образовавшийся на дне озера на глубине 5 м, всплывает на поверхность. Чему равна работа по всплыванию пузырька? Изменением объёма пузырька пренебречь. Плотность воды 1000 кг/м³. Ускорение свободного падения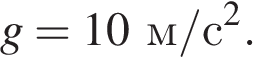 

Пояснение.

Обозначим:  h = 5 м, 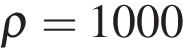 кг/м³,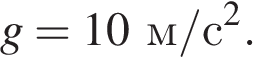 

Чтобы найти работу по всплыванию пузырька, нужно найти силу  Н. Следовательно, работа  Дж.

Ответ: A = 0,1 Дж.