Тема: Вводное повторение
Цель: повторить понятия одночлена, многочлена, арифметические действия с многочленами, формулы сокращенного умножения, различные способы разложения многочлена на множители.
Ход урока
Диагностическая работа
Вариант 1
Выполните действия:
(6 + 4х) + (5х - 3)
(4 + 3а) – (а + 5)
3х ( - 7х + 2)
- 7х + 2)
(2х + 1)(х - 1)


Разложите на множители:
х(а - b) – 5(а - b)
 - 25
- 25
 + ах + 2bх + 4b
+ ах + 2bх + 4b
Вариант 2
Выполните действия:
(6х + 4) + (7х - 3)
(3 + 10 b) – (b + 8)
4с( - 4с + 8)
- 4с + 8)
(3у + 2)(у - 2)


Разложите на множители:
у(с - х) -3(с - х)
16 - 
bу + 3b + 2су + 6с
Коррекционная работа
Повторение теоретического материала.
Опр. Одночленом называют произведение числовых и буквенных множителей.
Пример: аbс, 7 , -2
, -2
Опр. Стандартный вид одночлена – произведение числового множителя (коэффициента одночлена) и степеней различных переменных
Пример: 6ху, -0,7х ,
, 
Опр. Многочленом называют сумму одночленов
Пример: 5ху – 3х + 8, 2 - а + 7
- а + 7
Опр. Подобными членами многочлена называют те его члены, которые имеют одну и ту же буквенную часть.
Пример: 7 + 3 + 6а
+ 3 + 6а - 8
- 8 – 2, 10х – 8ху – 3ху.
– 2, 10х – 8ху – 3ху.
Опр. Для того, чтобы привести подобные члены многочлена, нужно сложить их коэффициенты и результат умножить на общую буквенную часть.
Пример: 5 + 2 + 4а
+ 2 + 4а - 3
- 3 - 7 =
- 7 =
Опр. Многочлен имеет стандартный вид, если каждый его член является одночленом стандартного вида и многочлен не содержит подобных членов.
Опр. Для того, чтобы записать алгебраическую сумму нескольких многочленов в виде многочлена стандартного вида, необходимо раскрыть скобки и привести подобные члены.
Опр. Если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобки.
Опр. Если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого на противоположный, заключенного в скобки.
Опр. Чтобы умножить многочлен на одночлен, нужно каждый член многочлена умножить на этот одночлен и полученные произведения сложить.
Пример: 9 ·(7
·(7 - 3n + 4) = 63
- 3n + 4) = 63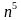 - 27
- 27 + 36
+ 36
Опр. Чтобы умножить многочлен на многочлен, нужно умножить каждый член одного многочлена на каждый член другого многочлена и полученные произведения сложить.
Пример: (3а - 2 )(-4
)(-4 +
+  ) = -12
) = -12  + 3а
+ 3а + 18
+ 18 - 2
- 2
Формулы сокращенного умножения:
 =
=  + 2аb +
+ 2аb + 
 =
=  - 2аb +
- 2аb + 
 =
=  + 3
+ 3 b + 3а
b + 3а +
+ 
 =
=  - 3
- 3 b + 3а
b + 3а -
- 
(а - b)(а + b) =  -
- 
 +
+  = (а - b)(
= (а - b)( + аb +
+ аb +  )
)
 -
-  = (а + b)(
= (а + b)( - аb +
- аb +  )
)
Способы разложения многочлена на множители:
вынесение общего множителя за скобки
применение формул сокращенного умножения
способ группировки
Самостоятельная работа:
Вариант1
Записать одночлен в стандартном виде:
4· ·6·аb
·6·аb
 ·36·
·36· ·
·
 у·7·
у·7· ·
·
 ·
·
-  b
b ·
·
 ·
·
Привести подобные члены многочлена:
- + 3
+ 3 - 4
- 4 + 3
+ 3 - 4
- 4
2 + 3 - 5
- 5 - 7
- 7 + 5
+ 5 - 2
- 2 – 9
– 9
8 у – 6х
у – 6х - 2
- 2 у +
у +  у – 3х
у – 3х
4а + 8
+ 8 - а
- а - 2
- 2 - 6
- 6 + 5
+ 5
Преобразовать в многочлен стандартного вида:
(1 + 5а) + ( - 3а)
- 3а)
( – b + 8) – (
– b + 8) – ( + b +9)
+ b +9)
(3 + 5х) + (-х + 6)
+ 5х) + (-х + 6)
(9 – 4
– 4 ) – (8 + 9
) – (8 + 9 – 3
– 3 )
)
( - 0,45а + 1,2) + (0,8
- 0,45а + 1,2) + (0,8 - 1,2а)–(1,6
- 1,2а)–(1,6 -2а)
-2а)
– (3а – аb + b) + 4а
– аb + b) + 4а - 5b – (6аb - а
- 5b – (6аb - а )
)
Выполните умножение:
3а( - 8а - 4)
- 8а - 4)
-4 (5
(5 - 3х - 2)
- 3х - 2)
( - 1,5у + 6) ·1,5у
- 1,5у + 6) ·1,5у
(3 -
-  + х)(- 5
+ х)(- 5 )
)
3аb·( - 4аb +
- 4аb +  )
)
-  b·(
b·( -
-  -
-  )
)
Выполните умножение:
(а + b)(х + у)
(х + 9)(у - 1)
(х + 6)(х + 5)
(5х - 3)(4 – 7х)
( + ху -
+ ху -  )(х + у)
)(х + у)
(5 – 2а +  )(4
)(4 - 3а - 1)
- 3а - 1)
Разложите многочлен на множители:
mх + mу + 6х + 6у
 +
+  + х+ 1
+ х+ 1
 у + х + х
у + х + х +у + 2ху + 2
+у + 2ху + 2
9 – 16
– 16
 - 8ах + 16
- 8ах + 16
 -
- 
 + 2ху +
+ 2ху +  -
- 
Вариант 2
Записать одночлен в стандартном виде:
3· ·5·ху
·5·ху
 ·32·
·32· ·
·
 ·8·
·8· ·
·
 ·
·
-  ·
·
 ·
·
Привести подобные члены многочлена:
- + 5
+ 5 - 6
- 6 + 8
+ 8 - 10
- 10
5 + 4 - 8
- 8 - 6
- 6 + 8
+ 8 - 3
- 3 – 6
– 6
9 b – 4а
b – 4а - 5
- 5 b +
b +  b – 2а
b – 2а
6 у + 9
у + 9 -
-  у - 7
у - 7 - 2
- 2 + 4
+ 4
Преобразовать в многочлен стандартного вида:
(3 + 8х) + ( – 10х)
– 10х)
( – 2b + 5) – (
– 2b + 5) – ( + 2b +7)
+ 2b +7)
(8 + 7а) + (-а + 9)
+ 7а) + (-а + 9)
(9 – 5
– 5 ) – (7 + 9
) – (7 + 9 – 4
– 4 )
)
( - 0,78х +2,3)+(0,7
- 0,78х +2,3)+(0,7 - 1,8х)–(1,3
- 1,8х)–(1,3 –3х)
–3х)
–(4 – а
– а )+3а
)+3а – 4а – (5а
– 4а – (5а -
-  b + а)
b + а)
Выполните умножение:
3b ( - 2
- 2 - 3)
- 3)
-5 (7
(7 – 4а - 3)
– 4а - 3)
( - 1,2у + 8) ·1,5у
- 1,2у + 8) ·1,5у
(5 -
-  + у)(- 3
+ у)(- 3 )
)
2аb·( - 3аb +
- 3аb +  )
)
-  ·(
·( -
-  -
-  )
)
Выполните умножение:
(m + х)(n + у)
(у - 4)(х + 2)
(а + 8)(а + 4)
(3у - 2)(5 – 6у)
( + аb -
+ аb -  )(а + b)
)(а + b)
(5 – 2х - 3)(4 – 3х +
– 2х - 3)(4 – 3х +  )
)
Разложите многочлен на множители:
аb + ас + 7b + 7с
1 + у+  +
+ 
 -b
-b - ах + аb +
- ах + аb +  - а
- а
25 - 4
 - 4bу + 4
- 4bу + 4
 -
- 
 - 10у +
- 10у +  -
- 
Решение уравнений
(23 + 3х) + (8х - 41) = 15
(19 + 2х)- (5х - 11) = 25
3,8 – 1,5у + (4,5у – 0,8) = 2,4у + 3
1,3 – 2 – (3,3х + 5) = 2х + 1
3(-2х + 1) – 2(х + 13) = 7х – 4(1 - х)
3у(4у - 1) – 2у(6у - 5) = 9у – 8(3 + у)
(3х - 2)(х + 4)- 3(х + 5)(х - 1) = 0
 + х(6 – 2х) = (х - 1)(2 - х) – 2
+ х(6 – 2х) = (х - 1)(2 - х) – 2
(х + 4)(х + 1) = х – (х - 2)(2 - х)
 –
–  =
= 
5 + 3х = 0
+ 3х = 0
у(у - 5) – 3у
 - 3
- 3 = (х + 3)(х - 3)
= (х + 3)(х - 3)
− 7 +
+  - 2 (4 + х)(х - 4) = 0
- 2 (4 + х)(х - 4) = 0
-  + 2(5 + х)(х - 5) + 7
+ 2(5 + х)(х - 5) + 7 = 3
= 3
Разложение на множители
18 – 2
– 2
2а - 16 а
- 16 а
8 + 8
+ 8 + 2
+ 2
9 - 6х – 10а - 25
- 6х – 10а - 25
 + 3
+ 3 х + 6ух + 12х – 8
х + 6ух + 12х – 8
 (х + 2у) – х – 2у
(х + 2у) – х – 2у
 (2у - 5) – 8у + 20
(2у - 5) – 8у + 20
 +
+  + 2ху – 1
+ 2ху – 1
 +
+  - 2аb – 25
- 2аb – 25
 -
-  -
-  + 2bс
+ 2bс
 +
+  + 2ху(х + у)
+ 2ху(х + у)
 -
-  - 5х(
- 5х( + ху +
+ ху +  )
)
 -
-  + 5
+ 5 b – 5а
b – 5а
 +
+  + 2
+ 2 - 2ху + 2
- 2ху + 2
 -
-  + 3
+ 3 + 3аb + 3
+ 3аb + 3
Решение задач
На путь из А в В пешеход тратит 35 мин. На обратный путь, увеличив скорость на 0,6 км/ч, он затратил на 5 минут меньше. Какое расстояние между А и В?
В саду растут яблони, груши и сливы. Всего плодовых деревьев 210. Число яблонь вдвое больше, чем груш, а груш вдвое больше, чем слив. Сколько деревьев каждого вида растет в саду?
Для изготовления бронзы берется 17 частей меди, 2 части цинка и одна часть олова. Сколько килограммов меди, инка и олова отдельно надо взять, чтобы изготовить 4 ц бронзы?
Туристический маршрут составляет 38 км. В первый день турист прошел вдвое больше, чем во второй, и на 8 км меньше, чем в третий. Сколько километров турист проходил каждый день?
Теплоход прошел расстояние между пунктами А и В по течению за 4 ч 30 мин, а из В в А против течения он прошел за 6 ч 18 мин. Какова скорость теплохода по течению, если скорость течения реки 2,4 км/ч?
В одном хранилище овощей было в 2 раза больше, чем в другом. Если в первое хранилище привезти еще 80 т овощей, а во второе – 145 т, то в обоих хранилищах овощей станет поровну. Сколько тонн овощей было в двух хранилищах первоначально?
Если от первого числа вычесть четверть второго числа, получится 129, а если увеличить второе число в 5 раз и отнять от него половину первого число, то получится первое число. Найти разность между большим и меньшим числами.
Домашнее задание
1 урок - № 20, 21, 106; 2 урок - № 22, 48, 143; 3 урок - № 170, 188, 190 (и - м)






 - 7х + 2)
- 7х + 2)

 - 25
- 25 + ах + 2bх + 4b
+ ах + 2bх + 4b - 4с + 8)
- 4с + 8)


 ,
, 
 + 3 + 6а
+ 3 + 6а ·(7
·(7 - 3n + 4) = 63
- 3n + 4) = 63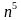 - 27
- 27 + 36
+ 36









