СВ 210 ЕН. 01 Математика
Преподаватель: Водяхина Н. В. Электронный адрес почты: nata.vodiahina2014@yandex.ru
Задание выдано 18.05.20. Задание выполнить до следующего занятия.
Законспектировать лекцию и разобрать примеры!
Тема: «Вычисление площадей плоских фигур и объемов тел вращения»
Цель: научиться вычислять площади плоских фигур и объемы тел вращения.
Вычисление площади плоской фигуры
При вычислении площадей плоских фигур с применением определенного интеграла мы рассмотрим следующие случаи:
1. Фигура ограничена непрерывной и неотрицательной на отрезке 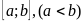 функции f(x), осью ОХ и прямыми
функции f(x), осью ОХ и прямыми 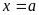 и
и 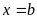 . В этом случае согласно геометрическому смыслу определенного интеграла площадь S фигуры численно равна
. В этом случае согласно геометрическому смыслу определенного интеграла площадь S фигуры численно равна 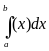 , т.е.
, т.е.
S= 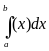 (1)
(1)
2. Фигура ограничена графиком непрерывной и неположительной на отрезке 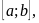
функции f (x), осью ОХ и прямыми 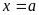 и
и 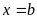
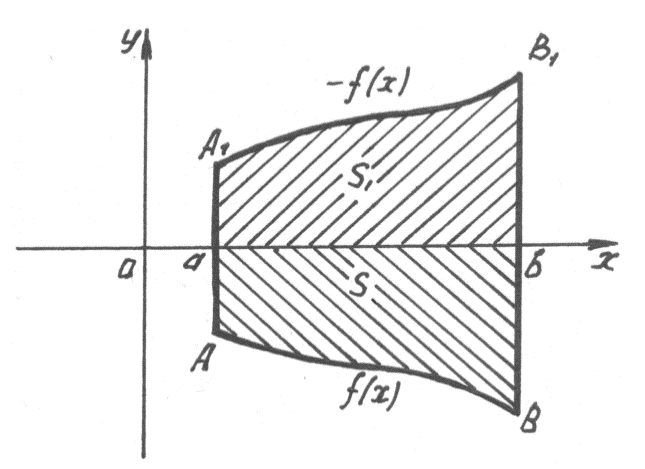
Рассмотрим функцию – f(x). Фигура аА1В1b симметрична фигуре аАВb относительно оси ОХ, а следовательно, их площади S1 и S равны.
Но
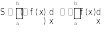
Поэтому
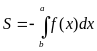 (2)
(2)
3. Фигура ограничена осью Ох, прямыми х = а , х = b и графиком функции f (x), которая непрерывна на отрезке 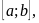 и меняет свой знак конечное число раз на этом отрезке. В этом случае разбивают отрезок
и меняет свой знак конечное число раз на этом отрезке. В этом случае разбивают отрезок 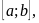 на такие частичные отрезки, на которых функция f (x) знакопостоянна на соответствующих отрезках. В нашем примере имеется три таких отрезка:
на такие частичные отрезки, на которых функция f (x) знакопостоянна на соответствующих отрезках. В нашем примере имеется три таких отрезка:
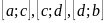 :
:
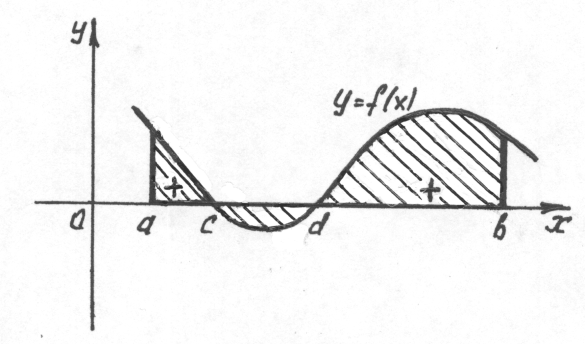
Очевидно, что искомая площадь S численно равна алгебраической сумме интегралов, взятых по каждому из полученных отрезков, причем знаки, с которыми эти интегралы входят в алгебраическую сумму, совпадают со знаками функции f (x) на соответствующих отрезках. Так, например, площадь фигуры, представленной на рисунке , вычисляется по формуле
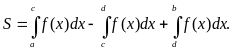
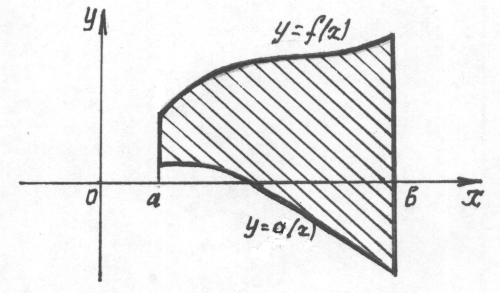
4. Фигура ограничена графиками двух непрерывных на отрезке 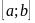 функций f(x) и g(x) и прямыми х = а , х = b,где
функций f(x) и g(x) и прямыми х = а , х = b,где 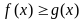 и
и 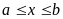 (рис. 52) В этом случае искомая площадь S вычисляется по формуле:
(рис. 52) В этом случае искомая площадь S вычисляется по формуле:
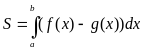 (3)
(3)
5. Фигура ограничена графиками трех и более непрерывных на отрезке 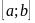 функций. В этом случае стараются искомую площадь представить в виде алгебраической суммы площадей, вычисление каждой из которых сводиться к одному из предыдущих четырех случаев. Так, например, площадь фигуры, изображенной на рисунке
функций. В этом случае стараются искомую площадь представить в виде алгебраической суммы площадей, вычисление каждой из которых сводиться к одному из предыдущих четырех случаев. Так, например, площадь фигуры, изображенной на рисунке
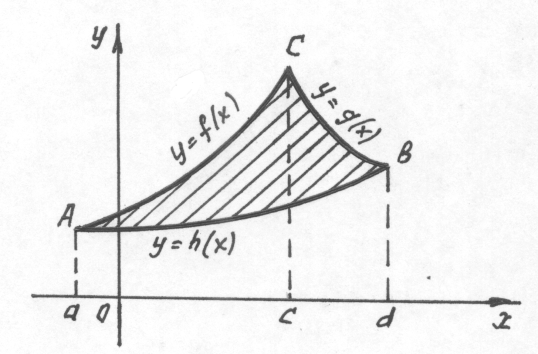
вычисляется по формуле 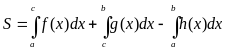
Вычисление объема тела вращения
Объем фигуры, образованной вращением вокруг оси ОХ криволинейной трапеции,
ограниченной кривой , осью Ох и прямыми х=а и х=b, вычисляется по формуле:
(4)
Аналогично, объем фигуры, образованной вращением вокруг оси ОУ криволинейной трапеции, ограниченной кривой , осью Ох и прямыми х=с и х=d, вычисляется по формуле
(5)
Примеры
Пример 1. Вычислить площадь фигуры, ограниченной линиями .
Решение: построим графики функций. Применив формулу (1), найдем площадь фигуры
Пример 2. Вычислить площадь фигуры, ограниченной линиями у = –х2 – 1, у = 0, х = –1. х = 2.
Решение: Построим графики заданных функций:
По формуле (2) находим
Пример 3. Вычислить площадь фигуры, ограниченной линиями y = sin x, y = 0, x = - /2, x =
/2, x =  .
.
Решение: очевидно, что  для всех
для всех  и
и  для всех
для всех  .
.
Поэтому:

Пример 4. Вычислить площадь плоской фигуры, ограниченной линиями
Из рисунка видно, что искомая площадь  или
или
Пример 5. Вычислить объем фигуры, образованной вращением площади, ограниченной линиями  , y=0 и х=4 вокруг оси Ох.
, y=0 и х=4 вокруг оси Ох.
Решение: выполним построение плоской фигуры. При вращении этой фигуры вокруг оси ОХ получим параболоид. Пределы интегрирования а=0 и b=4. По формуле (4) получим
(куб. ед.)
Пример 6. Вычислить объем фигуры, образованной вращением площади, ограниченной линиями  и у=0 вокруг оси Ох.
и у=0 вокруг оси Ох.
Р ешение: Выполним построение плоской фигуры. В силу симметрии фигуры относительно оси Оу возьмем пределы интегрирования от 0 до 3, а затем полученный результат удвоим. По формуле (4) находим






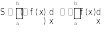
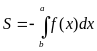 (2)
(2)
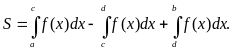
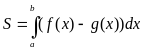 (3)
(3)