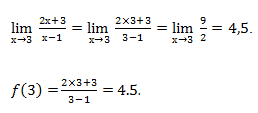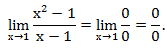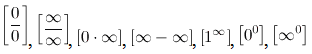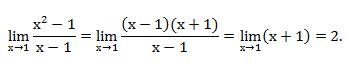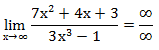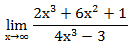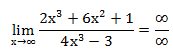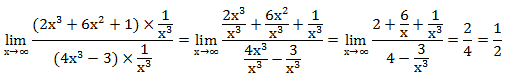Вычисление простейших пределов, 11 класс (теория+практика).

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Записывается предел следующим образом   .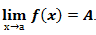

Вычислим предел: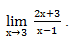 
Подставляем вместо х – 3.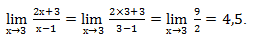
Заметим, что предел числа равен самому числу.

Примеры: вычислите пределы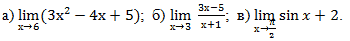 

Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной (в данной точке).

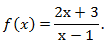
Вычислим значение функции в точке x₀ = 3 и значение его предела в этой точке.

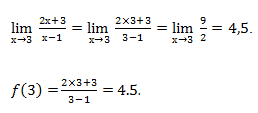
Значение предела и значение функции в этой точке совпадает, следовательно, функция непрерывна в точке x₀ = 3.

Но при вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.

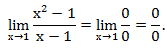
Основные виды неопределенностей: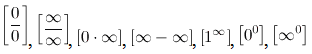  

Раскрытие неопределенностей

Для раскрытия неопределенностей используют следующее:

• упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;

• если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.

Пример: вычислим предел.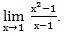
Разложим числитель на множители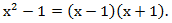 

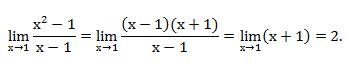
3. Вычисление пределов функции

 Пример 1. Вычислите предел функции: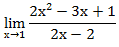 

При прямой подстановке, получается неопределенность:

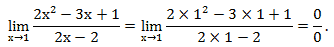
Разложим на множители числитель и знаменатель и вычислим предел.

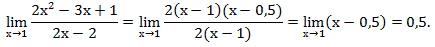
Пример 2. Вычислите предел функции: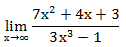 

При прямой подстановке, получается неопределенность.

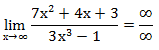
Помножим и числитель,  и знаменатель на  .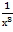

Учтем, что если число разделить на бесконечно большое число получится ноль. То есть предел 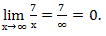 Аналогично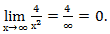   

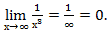
Пример 3. Вычислите предел функции: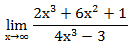 

При прямой подстановке, получается неопределенность.

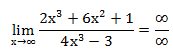
Помножим и числитель,  и знаменатель на  .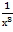

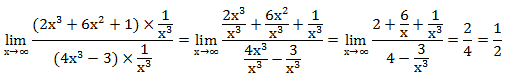
Мы учли, что 

4. Самостоятельные упражнения

Вычислите пределы:

6. Домашнее задание

Домашнее задание раздается на карточках каждому ученику.

Свойства пределов функции

1. Предел постоянной величины равен самой постоянной величине:

2. Предел суммы двух функций равен сумме пределов этих функций: Аналогично предел разности двух функций равен разности пределов этих функций.

3. Постоянный коэффициент можно выносить за знак предела:

4. Предел произведения двух функций равен произведению пределов этих функций:

5. Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

Замечание.Принято считать, что  Следующие пределы считают неопределенностью :  . Если в примере встретилась неопределенность, то надо найти пути для ее устранения. Общие правила:

1) если в числителе и знаменателе находятся многочлены , и имеется неопределенности вида   или  , то для решения нужно разложить числитель и знаменатель на множители или разделить на максимальную степень числителя (или знаменателя) и числитель и знаменатель;2) если же в числителе или в знаменателе находятся иррациональные выражения  и имеется неопределенности вида   или  , то для решения надо избавляться от иррациональности, помножив и числитель, и знаменатель на сопряженное выражение;3) если же в числителе или в знаменателе находятся тригонометрические выражения  и имеется неопределенности вида   или  , то для решения используют формулу замечательного предела 

Вычисление пределов функции

Пример 1.Найти предел функции:

Пример 2.Найти предел функции:

Пример 3.Найти предел функции:

Пример 4.Найти предел функции:

Пример 5.Найти предел функции:

Пример 6.Найти предел функции:

Пример 7.Найти предел функции:

Пример 8.Найти предел функции:

Пример 9.Найти предел функции:

Пример 10.Найти предел функции: Непрерывность функции Мы интуитивно понимаем, что если функция непрерывна, то мы можем ее нарисовать, не отрывая карандаша от листа бумаги.Функция у = f (x) называется непрерывной , если она непрерывна в каждой точке своей области определения.Чтобы понять, что такое непрерывность функции  в целом, сначала надо разобраться, что такое непрерывность функции в точке .Функция у = f (x) называется непрерывной в точке х = с, если предел функции в точке х = с равен значению функции в этой точке: Т.е. должны выполняться одновременно три условия:

1) функция определена и в самой точке х = с и в некоторой окрестности этой точки, причем U(с) ϵ D(f);2) существует  ;3) A = f(c).

Заметим, что в случае непрерывной функции в точке x = c, на графике данная точка выколотой быть не может.Для иллюстрации, как работает данное определение, рассмотрим три функции (см. табл.). Все три условия определения выполняются только у первой функции у = х + 1. У второй — не выполняется третье условие, а у третьей функции — первое.

Пример 11.Найти точку разрыва функции 

Решение

Найдем область определения функции: 5x + 7 ≠ 0, x ≠ -1,4.Ответ: -1,4.

Пример 12.Найти сумму значений точек разрыва функции 

РешениеНайдем область определения функции: х² + 2х — 3 ≠ 0. По теореме, обратной к теореме Виета: х₁ ≠ 1, x₂ ≠ -3.Далее находим сумму значений 1 + (-3) = -2.Ответ: -2.

Пример 13.Указать точку разрыва функции:

РешениеПостроим график данной функции на указанных промежутках. Видим, что целостность функции нарушается при х = 2.Ответ: 2.