| БЛОК 1. Вхождение в тему урока и создание условий для осознанного восприятия нового материала |
| Этап 1.1. Мотивирование на учебную деятельность |
| - Здравствуйте, ребята, начинаем наш урок. Какую тему мы изучаем? (Многогранники) - Коробка, небоскрёб, сэндвич, кристалл, медовые соты, холодильник имеют форму какого многогранника? (Призмы) |
| Этап 1.2. Актуализация опорных знаний |
|
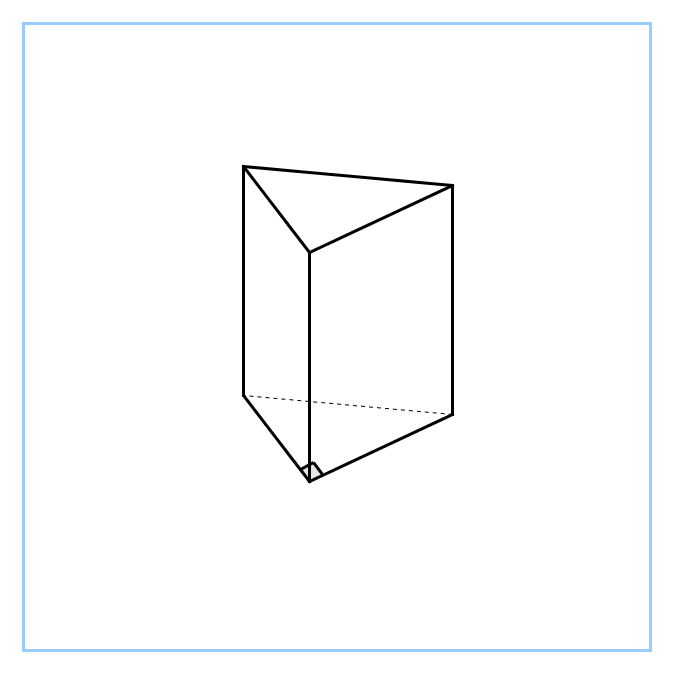
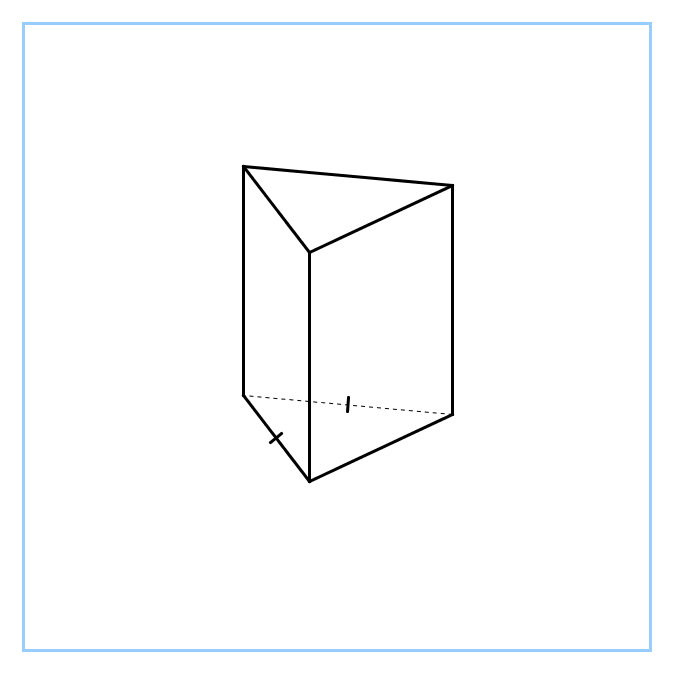
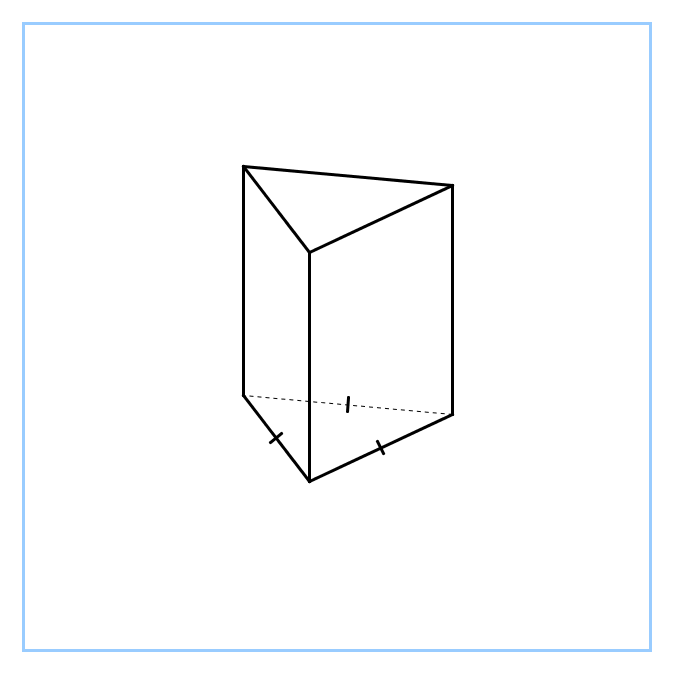
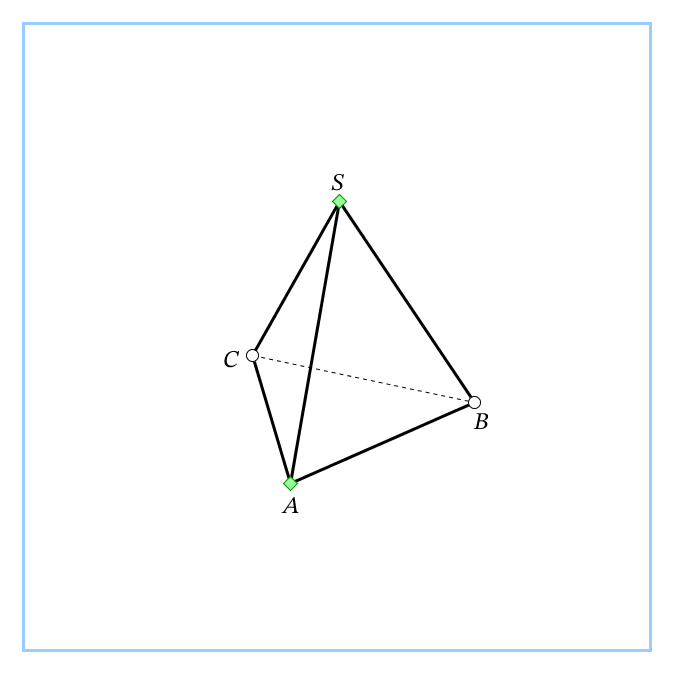
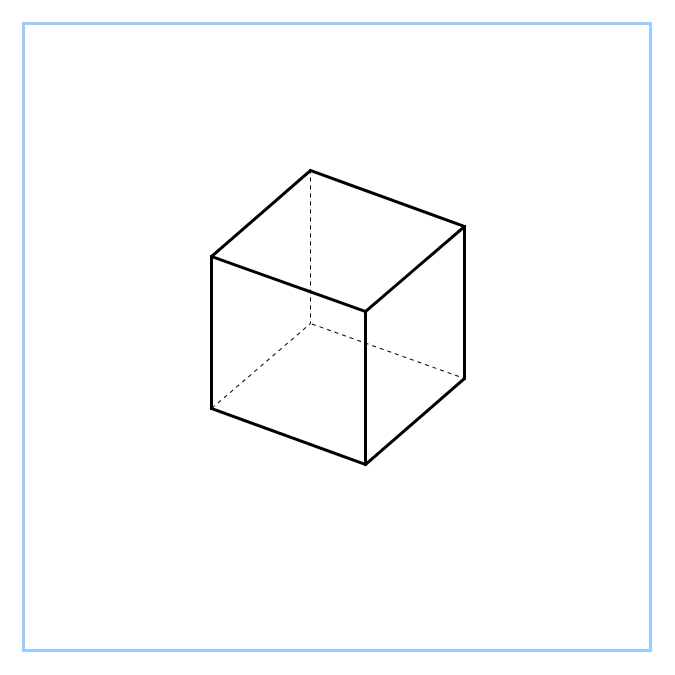
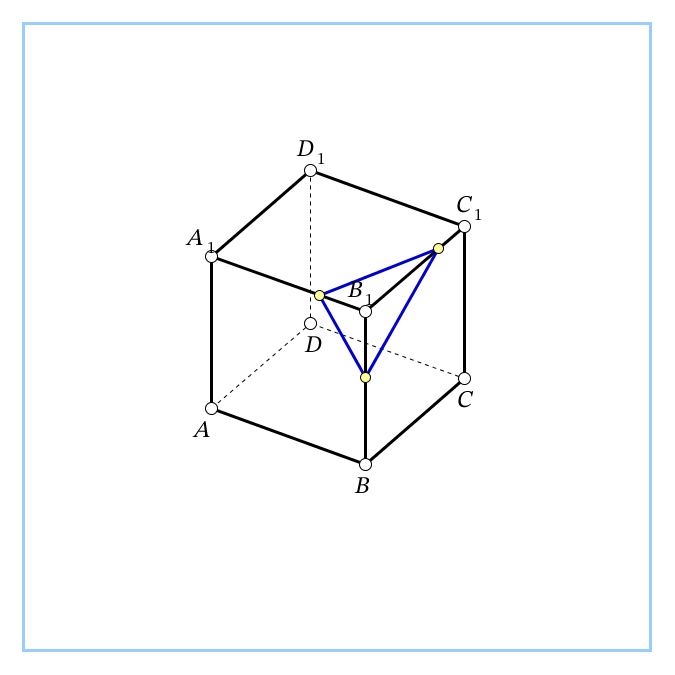
| Фронтальный опрос - Что мы о призме уже знаем? (Определение, изображение, виды, элементы) - Сформулируйте определение призмы - Перечислите виды призм по основанию по боковому ребру Мозговой штурм. - На доске три одинаковые призмы - Определите их вид (прямая, треугольная) - Давайте их сделаем разными 1) у первой в основании прямоугольный треугольник 2) у второй в основании равнобедренный треугольник 3) а третья – правильная - Какой можно сделать вывод? (Рисунок одинаковый, разными его делают обозначения, они очень важны) - Сформулируйте определение правильной призмы - Назовите элементы призмы (грани, рёбра, вершины) - Какое наименьшее число граней может иметь многогранник? (4) - Как называется такой многогранник? (тетраэдр) Появляется модель на доске - Сколько у него рёбер и вершин? (рёбер – 6, вершин – 4) - Дан куб - Сколько у куба граней, рёбер, вершин? (Граней – 6, рёбер – 12, вершин – 8) - У куба отпилили уголок. Сделайте рисунок и определите, сколько граней, рёбер и вершин у полученного тела. (Граней – 7, рёбер – 15, вершин – 10). - Вспомните, что изучали в 10 классе до многогранников? (параллельность и перпендикулярность в пространстве) - Что вычисляли? (сечения, расстояния и углы в пространстве) - Да, учились их строить, видеть, вычислять | 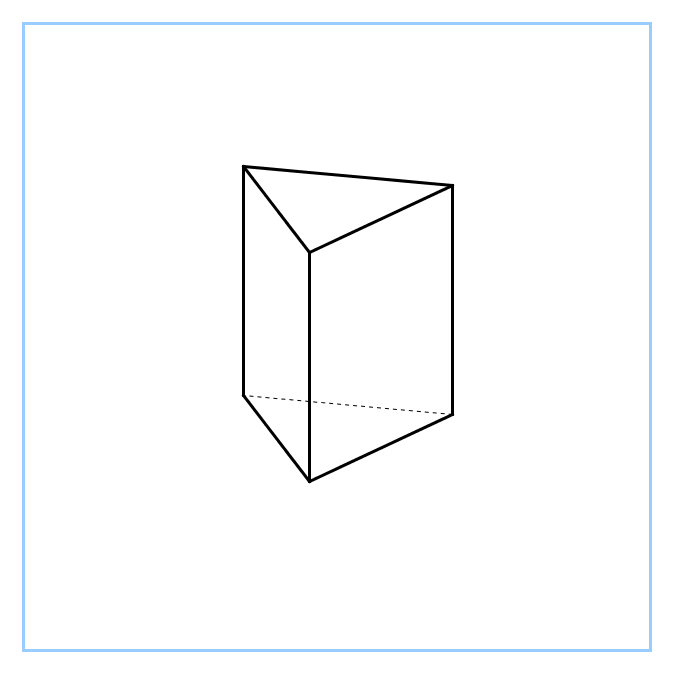  
|
| Этап 1.3. Целеполагание |
| Ребята формулируют тему - Какие цели вы поставите перед собой? (Научиться применять полученные знания и умения для призмы) |
| БЛОК 2. Постановка проблемы и поиск путей решения проблемы |
| Этап 2.1. Осуществление учебных действий в изменённых условиях |
|
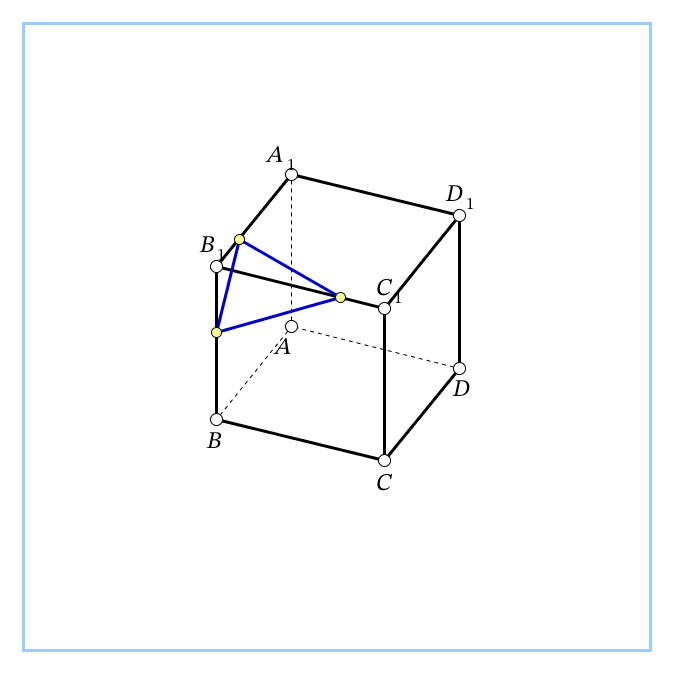
| Учебная проблема: учиться вычислять расстояние между точками, от точки до прямой, от точки до плоскости в призме. Учебная ситуация 1 Дана прямая 4-угольная призма ABCDA1B1C1D1, в основании которой прямоугольник. АВ=1, AD=8, AA1=4. Учащимся предоставляется модель призмы. Вопросы к учащимся: 1. Вычислите расстояние между точками А1 и С. (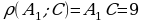 ). Ответ: 9. ). Ответ: 9. 2. Вычислите расстояние от точки В до прямой А1С. (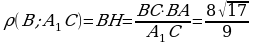 , где ВН – высота ▲ВСА1). Ответ: , где ВН – высота ▲ВСА1). Ответ: 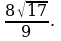 3. Вычислите расстояние от точки А1 до плоскости ВСС1В1. (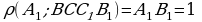 ). Ответ: 1. ). Ответ: 1. Вывод: расстояния в 4 –угольной призме вычислить несложно. Хочется рассмотреть и другие задачи на эти расстояния. | 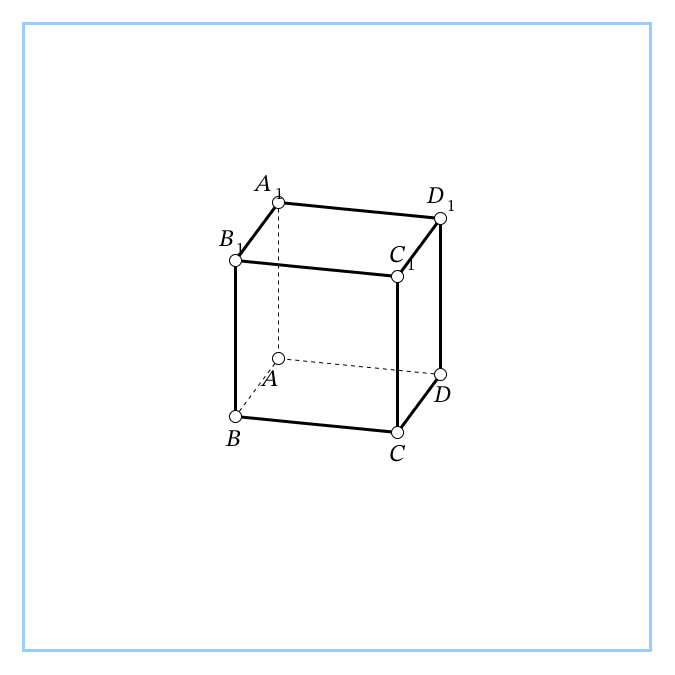 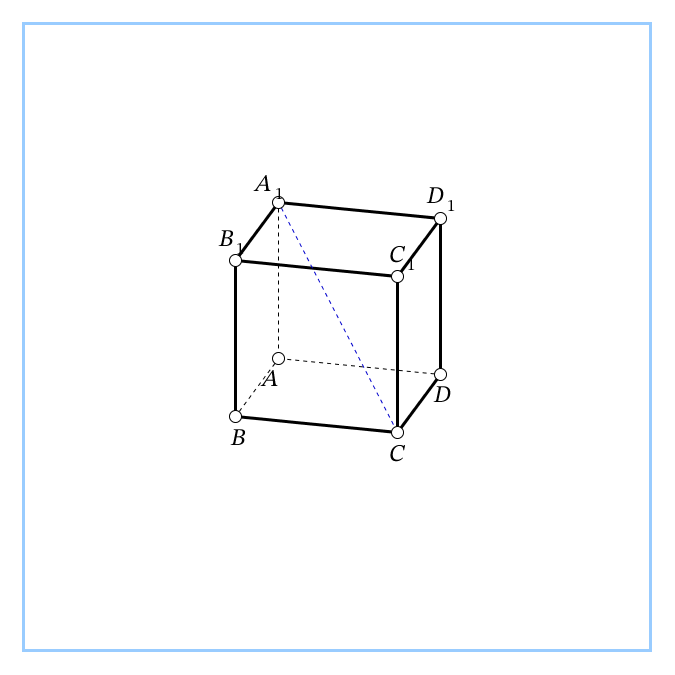 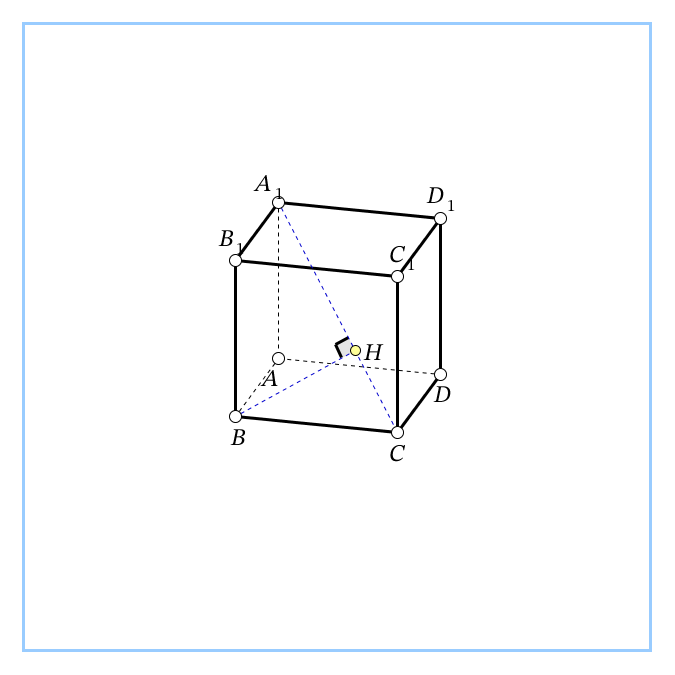 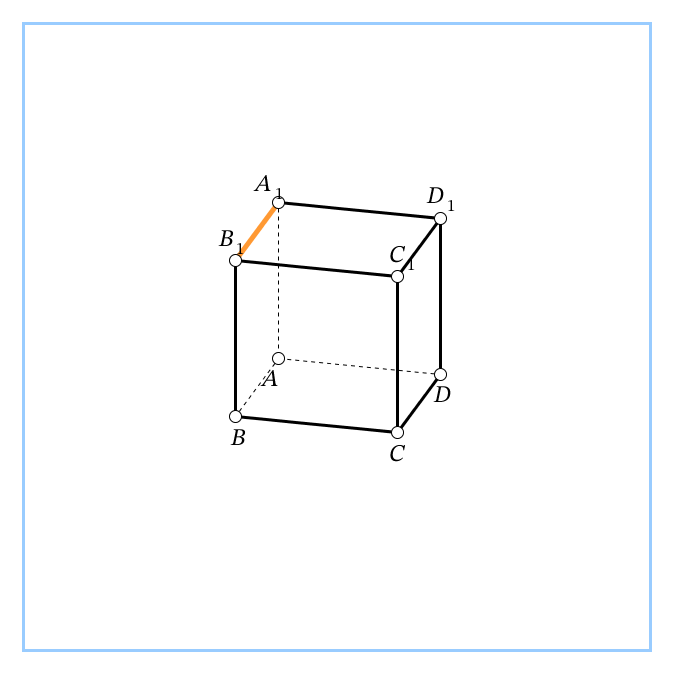
|
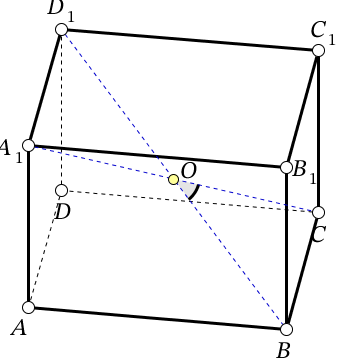
| Учебная ситуация 2 - Какие углы в пространстве мы считаем? (между прямыми пересекающимися или скрещивающимися, между прямой и плоскостью, между плоскостями 1. В правильной 4-угольной призме ABCDA1B1C1D1 известно, что А1С=2АВ. Найдите угол между диагоналями А1С и В1D.
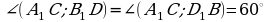 Ответ: 60º. Ответ: 60º.
| 
|
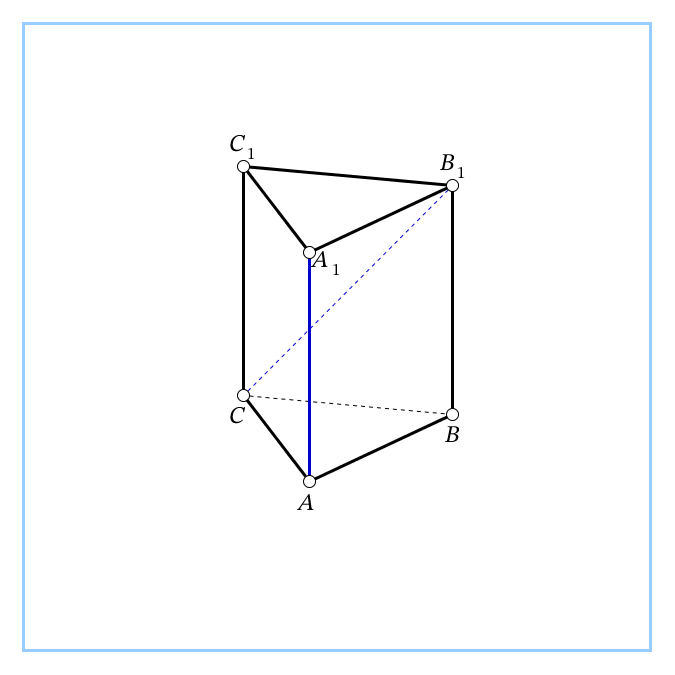
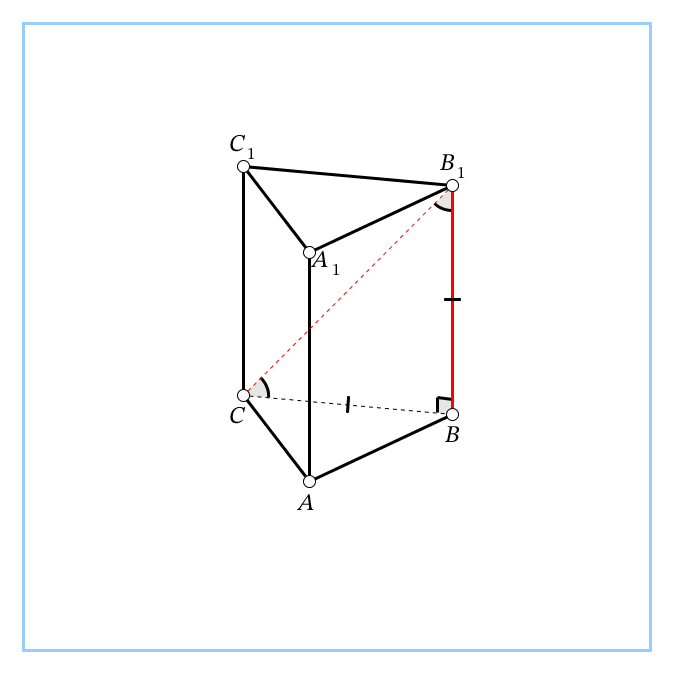
| 2. В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 6, найти угол между прямыми АА1и СВ1.
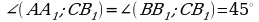 , т.к. АА1 ll ВВ1. Ответ: 45°. , т.к. АА1 ll ВВ1. Ответ: 45°.

|  
|
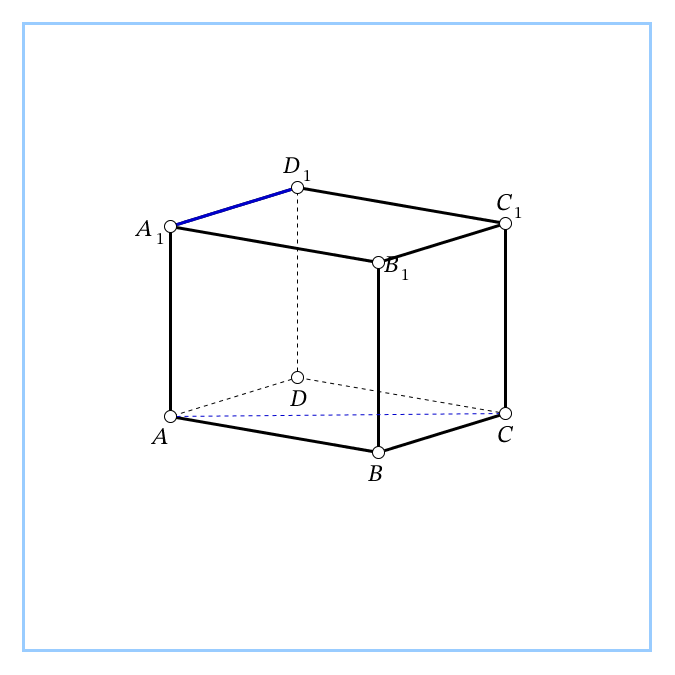
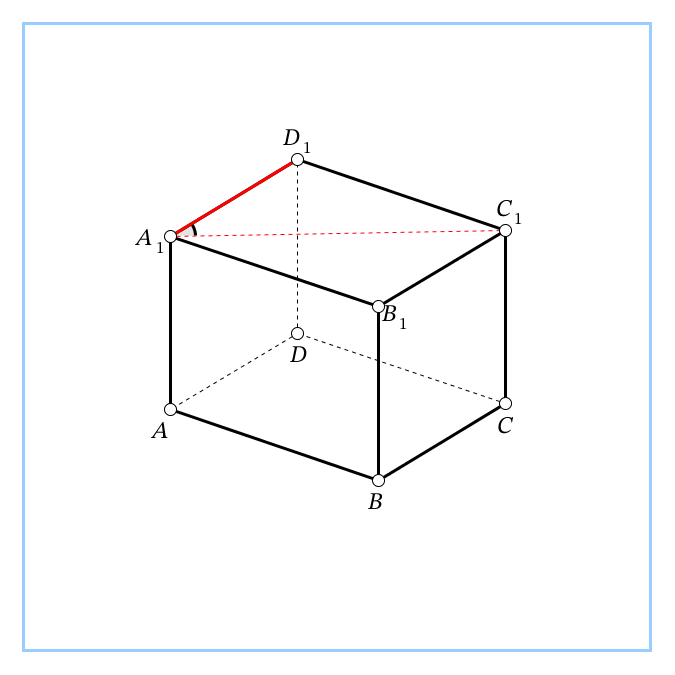
| 3. В основании прямой 4-угольной призмы ABCDA1B1C1D1 – прямоугольник. Известны длины рёбер АВ=6, АD=8, АА1=21. Найти синус угла между прямыми АС и А1D1.
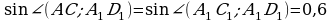 , т.к. А1С1llАС. Ответ: 0,6. , т.к. А1С1llАС. Ответ: 0,6.
|   |
| 4. В правильной 4-угольной призме ABCDA1B1C1D1 все рёбра равны 6. Найти угол между прямой ВD1 и плоскостью АВС.
Ответ: 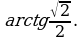 | 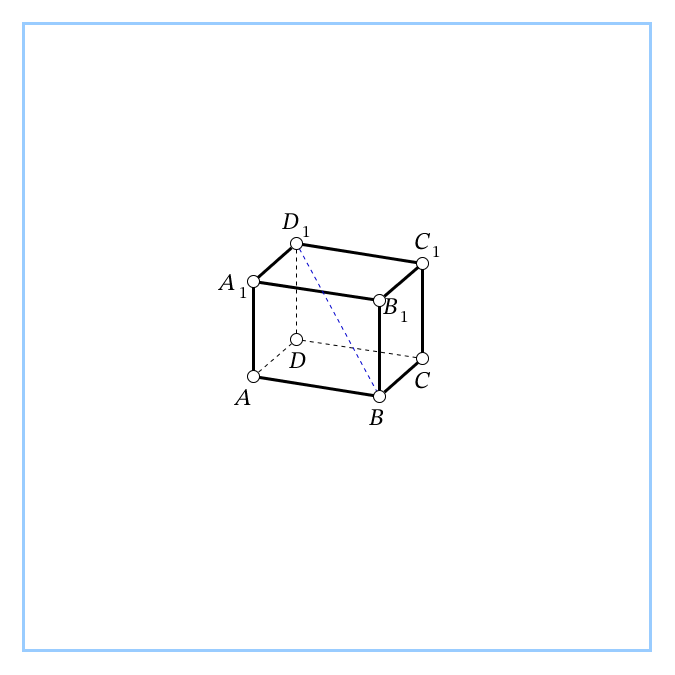 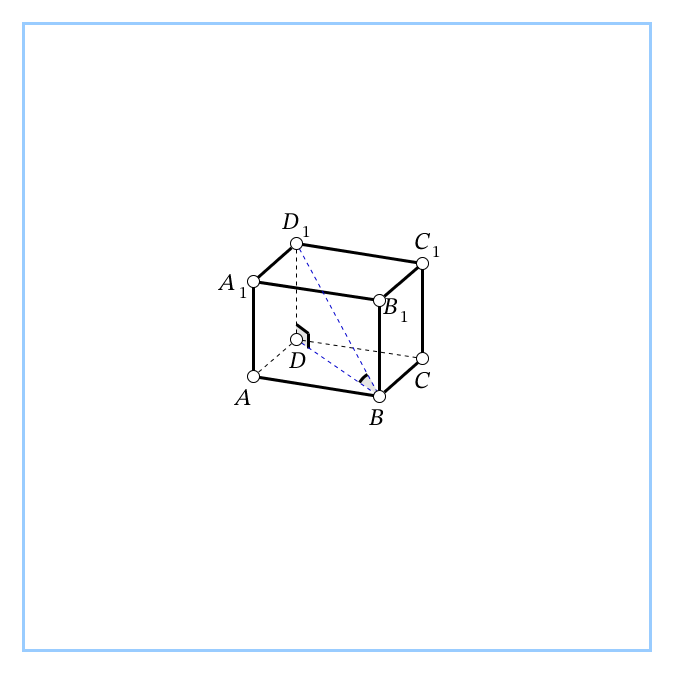 |
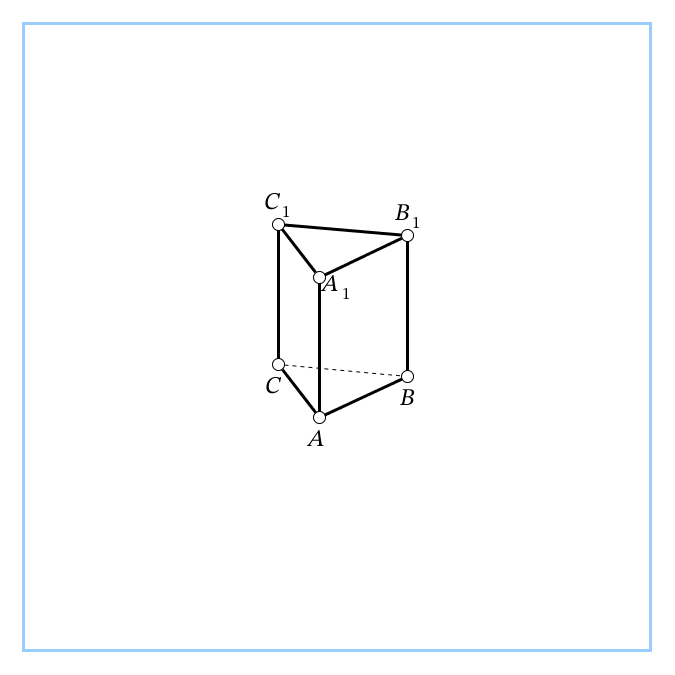
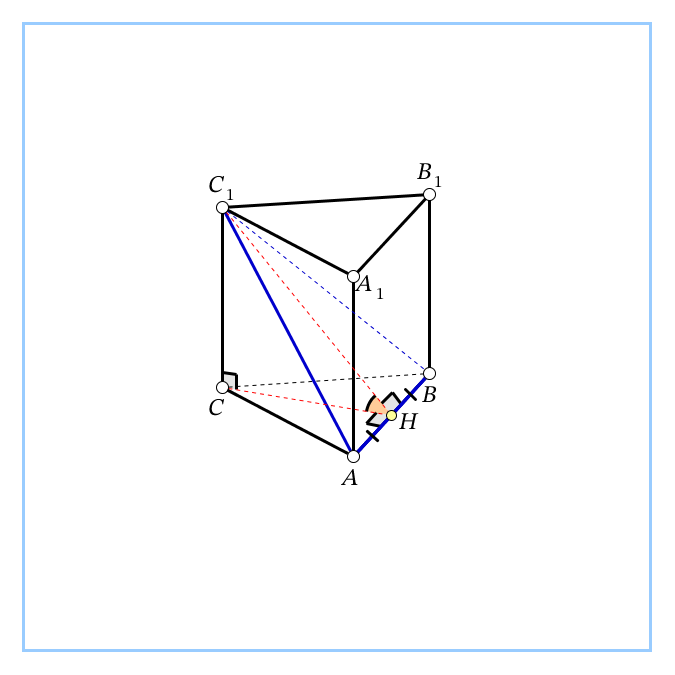
| 5. В правильной треугольной призме все рёбра равны 6. Постройте сечение призмы плоскостью, проходящей через ребро нижнего основания и противоположную вершину верхнего основания. Определите вид сечения. Вычислите площадь сечения. Найдите угол между плоскостью сечения и плоскостью основания. С1А=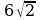 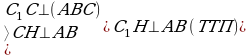 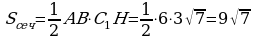 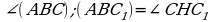 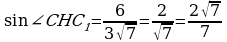 Ответ: 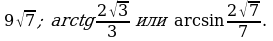
|  
|
| Вывод: все расстояния, углы и площади сечений можно вычислять в призме, это интересно, надо порешать еще задач. Рассмотреть пример с шестиугольной призмой. |
| Этап 2.2. Проверка усвоения |
| Пожалуй, самым сложным случаем является случай вычисления угла и расстояния между скрещивающимися прямыми. Используя приобретенные новые знания, ответьте на вопросы: - как вычислить угол между скрещивающимися рёбрами в прямой призме? (Найти угол между пересекающимися прямыми, параллельными данным скрещивающимся). - как вычислить расстояние между скрещивающимися прямыми в призме? (Решение может включать построение общего перпендикуляра к прямым и вычисление его длины). |
| БЛОК 3. Применение изученного материала |
| Этап 3.1. Применение знаний, в том числе в новых ситуациях |
| Самостоятельно разобрать и записать решение задачи - В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 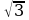 , нужно найти расстояние между прямыми AA₁ и BC₁ и угол между ними. Ответ: 1,5; 45°. , нужно найти расстояние между прямыми AA₁ и BC₁ и угол между ними. Ответ: 1,5; 45°. |
| Этап 3.2. Выполнение заданий в формате ГИА (ОГЭ, ЕГЭ) |
| Базовый уровень | Профильный уровень |
|
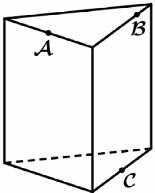 1. Плоскость, проходящая через три точки A, B и C, разбивает правильную треугольную призму на два многогранника. Сколько вершин у получившегося многогранника с меньшим числом граней? 1. Плоскость, проходящая через три точки A, B и C, разбивает правильную треугольную призму на два многогранника. Сколько вершин у получившегося многогранника с меньшим числом граней?
|
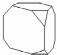 2. От деревянной правильной треугольной призмы отпилили все её вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые рёбра на рисунке не изображены)? 2. От деревянной правильной треугольной призмы отпилили все её вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
|
| Ответ: 6; 18. | | 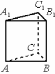 1. В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 2, найдите угол между прямыми BB1 и AC. 1. В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 2, найдите угол между прямыми BB1 и AC.
| 2. 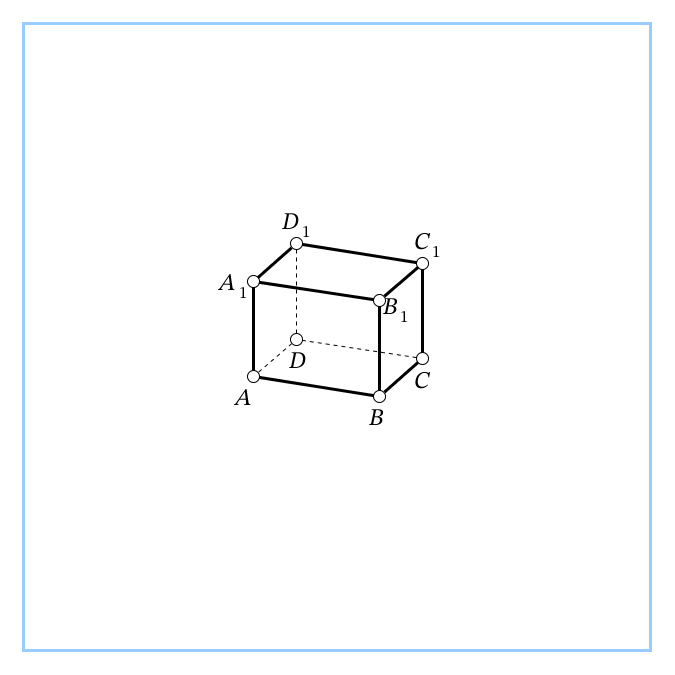 В прямой 4-угольной призме ABCDA1B1C1D1 известны длины рёбер: AB=28, AD=16, AA1=12. Найдите синус угла между прямыми DD1 и B1C. В прямой 4-угольной призме ABCDA1B1C1D1 известны длины рёбер: AB=28, AD=16, AA1=12. Найдите синус угла между прямыми DD1 и B1C. Ответ: 90º; 0,8. |
| Этап 3.3. Развитие функциональной грамотности |
| 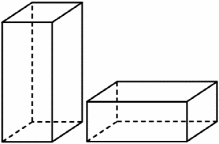 Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в два раза выше второй, а вторая втрое шире первой. Вместимость какой коробки больше? (Второй) Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в два раза выше второй, а вторая втрое шире первой. Вместимость какой коробки больше? (Второй)
|
|
| БЛОК 4. Проверка приобретенных знаний, умений и навыков |
| Этап 4.1. Диагностика/самодиагностика |
| Работа в парах. 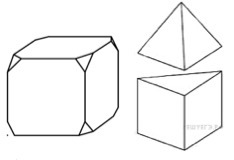 - От деревянного куба отпилили все его вершины. Сколько вершин у получившегося многогранника? - От деревянного куба отпилили все его вершины. Сколько вершин у получившегося многогранника? - К правильной треугольной призме приклеили правильную треугольную пирамиду так, что основания совпали. Сколько граней у получившегося многогранника? |
| БЛОК 5. Подведение итогов, домашнее задание |
| Этап 5.1. Рефлексия |
| Продолжите высказывания об уроке. 1. Мне понравился сегодняшний урок тем… 2. Для меня тема трудная, вот если бы… 3. Для меня тема легкая, и я … |
| Этап 5.2. Домашнее задание. Задачи на карточках |
| База | Профиль |
| 1. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах. 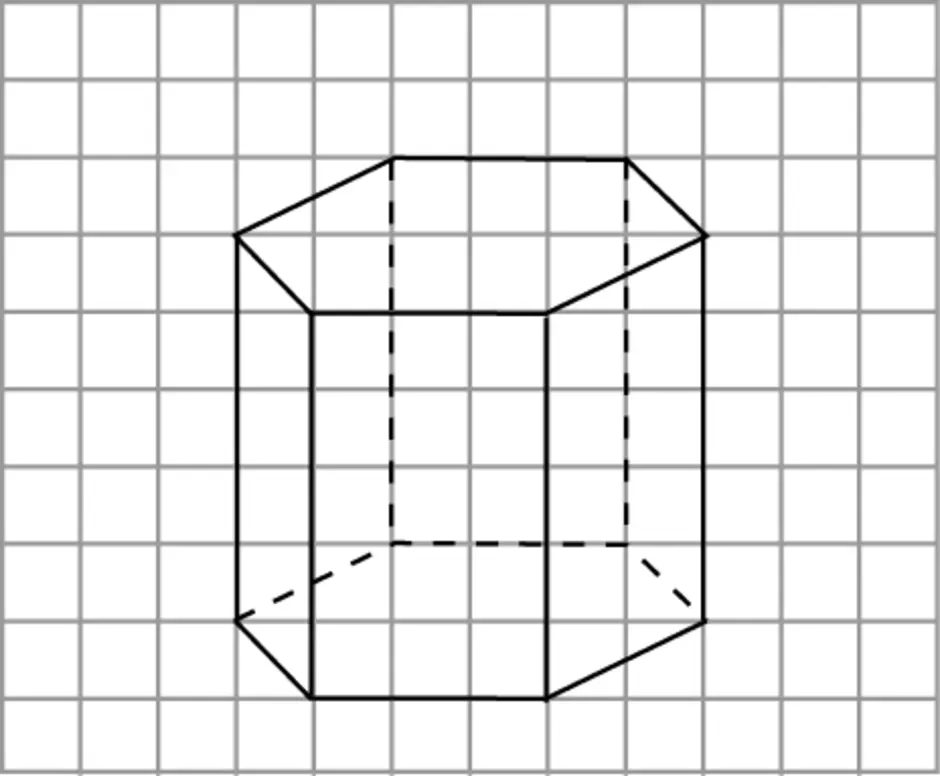 2. Вычислите количество проволоки для изготовления каркаса в виде правильной шестиугольной призмы, все рёбра которой равны 10 см. 2. Вычислите количество проволоки для изготовления каркаса в виде правильной шестиугольной призмы, все рёбра которой равны 10 см.
Ответ: 60°, 180 см. | 1. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все рёбра которой равны 1, нужно найти угол между прямыми АА₁ и Е₁С.  2. В основании прямой треугольной призмы прямоугольный равнобедренный треугольник. Катеты основания 6, боковое ребро 8. Постройте сечение призмы плоскостью, проходящей через катет нижнего основания и противоположную вершину верхнего основания. Определите вид сечения и его площадь. Найдите угол между плоскостью сечения и плоскостью основания. Ответ: 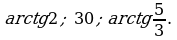 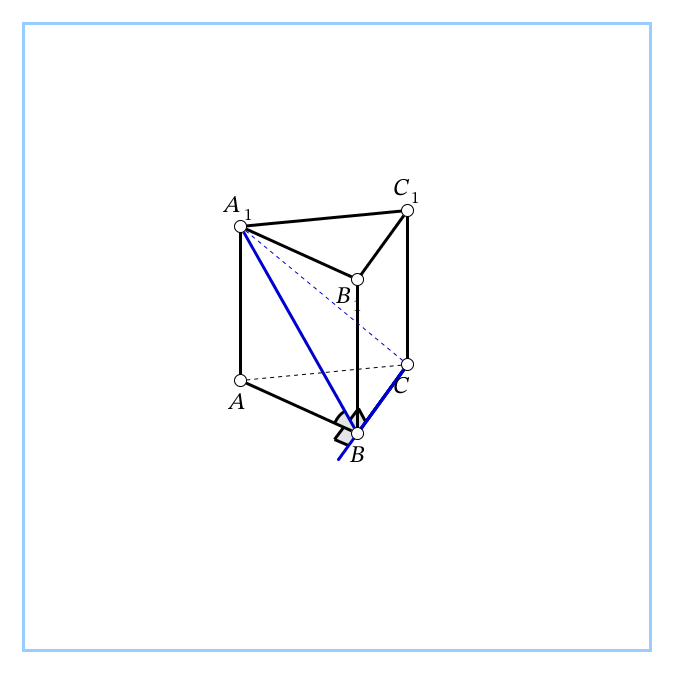 |















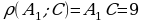 ). Ответ: 9.
). Ответ: 9.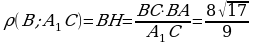 , где ВН – высота ▲ВСА1). Ответ:
, где ВН – высота ▲ВСА1). Ответ: 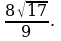
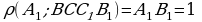 ). Ответ: 1.
). Ответ: 1.



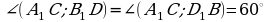 Ответ: 60º.
Ответ: 60º.
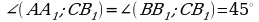 , т.к. АА1 ll ВВ1. Ответ: 45°.
, т.к. АА1 ll ВВ1. Ответ: 45°.


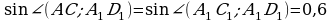 , т.к. А1С1llАС. Ответ: 0,6.
, т.к. А1С1llАС. Ответ: 0,6.

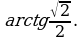


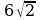
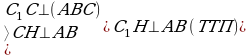
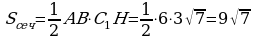
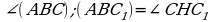
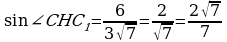
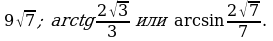


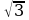 , нужно найти расстояние между прямыми AA₁ и BC₁ и угол между ними. Ответ: 1,5; 45°.
, нужно найти расстояние между прямыми AA₁ и BC₁ и угол между ними. Ответ: 1,5; 45°. 1. Плоскость, проходящая через три точки A, B и C, разбивает правильную треугольную призму на два многогранника. Сколько вершин у получившегося многогранника с меньшим числом граней?
1. Плоскость, проходящая через три точки A, B и C, разбивает правильную треугольную призму на два многогранника. Сколько вершин у получившегося многогранника с меньшим числом граней?  2. От деревянной правильной треугольной призмы отпилили все её вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
2. От деревянной правильной треугольной призмы отпилили все её вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые рёбра на рисунке не изображены)?  1. В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 2, найдите угол между прямыми BB1 и AC.
1. В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 2, найдите угол между прямыми BB1 и AC.  В прямой 4-угольной призме ABCDA1B1C1D1 известны длины рёбер: AB=28, AD=16, AA1=12. Найдите синус угла между прямыми DD1 и B1C.
В прямой 4-угольной призме ABCDA1B1C1D1 известны длины рёбер: AB=28, AD=16, AA1=12. Найдите синус угла между прямыми DD1 и B1C.  Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в два раза выше второй, а вторая втрое шире первой. Вместимость какой коробки больше? (Второй)
Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в два раза выше второй, а вторая втрое шире первой. Вместимость какой коробки больше? (Второй) - От деревянного куба отпилили все его вершины. Сколько вершин у получившегося многогранника?
- От деревянного куба отпилили все его вершины. Сколько вершин у получившегося многогранника? 2. Вычислите количество проволоки для изготовления каркаса в виде правильной шестиугольной призмы, все рёбра которой равны 10 см.
2. Вычислите количество проволоки для изготовления каркаса в виде правильной шестиугольной призмы, все рёбра которой равны 10 см.