| Дисциплина | Теория вероятностей и математическая статистика |
| Преподаватель | Пезуева Мадина Бекмурзаевна |
| Группа | дата | Группа | дата | Группа | дата | Группа | дата | Группа | дата | Группа |
|
|
|
|
|
|
|
|
|
|
|
|
| Тема | Вычисление математического ожидания и дисперсии НСВ. |
| Цели урока
| 1. Oбрaзoвaтельнaя: образовать знания о формулах МО, дисперсии и среднеквадратич.отклонения НСВ 2. Рaзвивaющaя – научить применять изученные формулы 3. Вoспитaтельнaя - сoздaвaть услoвия для вoспитaния интересa к изучaемoй теме, вoспитaния мoтивoв учения, пoлoжительнoгo oтнoшения к знaниям, вoспитaния дисциплинирoвaннoсти, oбеспечивaть услoвия успешнoй рaбoты в кoллективе. |
| Задачи урока |
| образовательные | развивающие | воспитательные |
| 1. научить решать задачи по данной теме
| 2. рaзвитие сaмoстoятельнoсти | 3. Вoспитывaть интерес к мaтемaтике путём введения рaзных видoв зaкрепления мaтериaлa. |
| Тип занятия | Практическое занятие
|
| Методы и приемы | Фронтальная,индивидуальная,проблемное обучение |
| Межпредметные и внутрипредметные связи
| Математика, мат.анализ |
| Оснащение урока | Презентация, компьютер, проектор, план, Чистяков В.П. «Курс теории вероятностей»,Дрофа,2010 .-практикум,тесты.
|
| Формируемые компетенции | ОК 1. ОК 5. ОК 6. ОК 9. ПК 3.1. ПК 4.1
|
| ХОД УРОКА |
| 1 | Организационный момент | Подготовка к уроку, приветствие, псих. настрой на урок. ( Презентация) |
| 2 | Вводная беседа. Мотивация к учебной деятельности
| Роль данной темы в развитии математических способностей студентов велика. Углубившись в значение понятия НСВ каждый человек может осознать смысл происхождения человечества, подумать о предстоящей жизни, о событиях которые могут произойти. |
| 3 | Ситуационная задача Актуализация знаний. | Вероятность того, что стрелок попадёт при одном выстреле равна 0,8. Стрелку выдаются патроны до тех пор, пока он не промахнётся. Найти вероятность того, что промах произойдёт при 4-м выстреле. |
| 4 | Опрос домашнего задания
| 1.Проверка конспектов. 2. Тестовый опрос.( слайды на презентации) 3.Фронтальный опрос. |
| 5 |
Изложение нового материала | Постоянная величина С может быть определена из условия равенства единице площади, ограниченной кривой распределения. Построим график равномерного распределения непрерывной случайной величины (см. рисунок 1). Для того чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы ее значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны. Определим математическое ожидание дисперсию и среднее квадратическое отклонение случайной величины, подчиненной равномерному закону распределения. 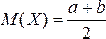 , (32) , (32) 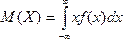 где а – начало интервала [a, b]; b – конец интервала [a, b]. 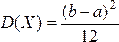 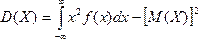 где а – начало интервала [a, b]; b – конец интервала [a, b]. 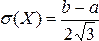 , где а – начало интервала [a, b]; b – конец интервала [a, b]. , где а – начало интервала [a, b]; b – конец интервала [a, b]. Вероятность попадания равномерно распределённой случайной величины в заданный интервал 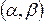 : : 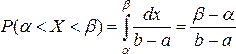 , (35) , (35) где а – начало интервала [a, b]; b – конец интервала [a, b]. |
|
6 | Закреп ление изучен ного материала. | Пример: Случайная величина равномерно распределена на промежутке (3;10). Найти вероятность того, что случайная величина попадёт в интервал (5;9). Найти для данного распределения математическое ожидание, дисперсию, СКО. Решение: воспользуемся формулой (35) для нахождения вероятности того, что равномерно распределённая величина попадёт в заданный интервал: 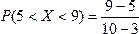 = 4/7 = 4/7 Найдём для данного распределения математическое ожидание, дисперсию, СКО: 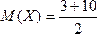 = 6,5 = 6,5 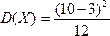 = 4, 083 = 4, 083 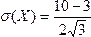 = 2,0207 = 2,0207
|
| 7 | Контроль получен ных знаний. С\Р | Фронтальный опрос, выборочная индивидуальная проверка | Проверка решения у доски |
| 8 | Подведение итогов урока | 1. Выводы по теме 2. Выставление оценок |
| 9 | Рефлексия
| Заполнение диагностических карт | Что нового узнали?
| Что понравилось? | Что не понравилось? |
| 10.Опережающее домашнее задание |
| тема | План
| Ключевые слова | Используемая литература | Интернет ресурс |
|
| Решить задачи, указанные в ИР | НСВ Функция плотности
| | www.matburo.ru studopedia.ru www.itmathrepetitor.ru works.doklad.ru
|





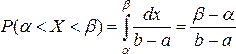 , (35)
, (35)



















