Вычисление площади многоугольника

ВЫЧИСЛЕНИЕ ПЛОЩАДИ МНОГОУГОЛЬНИКА

Формула Пика

МОУ СШ№72 ВОЛГОГРАД

Площадь вписанного в окружность четырёхугольника вычисляется по формуле Брахмагупты.

Формула Симпсона где b 1 - длина нижнего основания, b 2 - длина среднего основания, b 3 - длина верхнего основания, h – высота фигуры.

Рис. 9

рис

Рис. 11

Палетка – прозрачная пленка, разделенная на одинаковые квадраты: это могут быть квадратные дециметры, квадратные сантиметры, квадратные миллиметры.

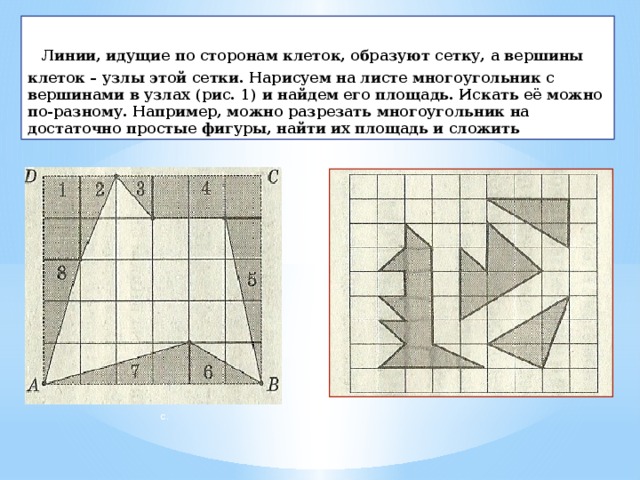
Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах (рис. 1) и найдем его площадь. Искать её можно по-разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площадь и сложить

с.

Георг Александр Пик

(10 августа 1859 - 13 июля 1942) -австрийский математик, родился в еврейской семье.

Мать - Йозефа Шляйзингер, отец -Адольф Йозеф Пик.

Георга, который был одарённым ребёнком, обучал отец, возглавлявший частный институт.

Пик вывел формулу для нахождения площади многоугольников, вершины которых лежат в узлах клетчатой бумаги.

Формула была открыта в 1899 году

Треугольника

Прямоугольника

Квадрата

Параллелограмма

Ромба

Трапеции

Многоугольника

Формула ПИКА

МЕТОД УЗЛОВ ДЛЯ ВЫЧИСЛЕНИЯ ПЛОЩАДИ :

Основное условие для применения формулы Пика :

у многоугольника, изображённого на клетчатой бумаге ( решётка), должны быть только целочисленные вершины, то есть они обязательно должны находиться в узлах решётки.

S= В + Г/2 -1,

где В - количество точек внутри многоугольника

Г — количество точек на границе многоугольника.

Разносторонние треугольники

площадь прямоугольника и ромба S = В + Г/2- 1

Параллелограмм

Трапеция, шестиугольник и пятиугольник

Получаем, S = 28 + 20/2 - 1 = 37 кв.ед.

Задача 1

Г = 8 В = 1

S = 1 + 8/2 – 1 = 1 + 4 – 1

Ответ: 4

ВЫВОД:

• Для вычисления площади многоугольника, нужно знать всего одну формулу: S = В + Г/2 - 1 - формулу Пика.
• Формула Пика проста для запоминания.
• Формула Пика удобна и проста в применении.
• Многоугольник, площадь которого необходимо вычислить, может быть любой формы.