Тема урока: «Вынесение общего множителя за скобки».
Класс: 7 «В» 27.01.2022
Тип урока: обобщающий
Цели:
-
Обобщить и закрепить знания, по теме: «Разложение на множители вынесением общего множителя за скобки».
-
Содействовать развитию умений и навыков по теме, мышления, речи, памяти, умение выделять главное, оценивать значения.
-
воспитывать уважение друг к другу при работе в коллективе, аккуратность
Ход урока:
Сегодня на уроке мы завершаем тему: «Вынесение общего множителя за скобки»
Давайте решим какие цели мы ставим перед собой на этот урок. (цели говорят дети)
-
Разминка
На партах лежат листочки для устного счета. За 1 минуту каждый вариант решает примеры устно, а второй оценивает с помощью светофоров
-
Проверка домашнего задания:
№31.17(а), №31.18(а), №31.19(б), №31.20(а,б), №31.25(а)
Ответы: №31.17(а) 0;3
№31.18(а) 0; -0,4
№31.19(б) (х – 6)(х – 6 + 2х) = 0
(х – 6)(3х – 6) = 0
6; 2
№31.20(а,б) 154 · (154 + 46) = 154 · 200 = 30 800
0,22 · (0,2 + 0,8)= 0,04
№31.25(а) 175· (17 +1) = 175 · 18 ⁞ 18
-
1 чел. У доски: Вынести общий множитель:
-
8a – 16b
-
5x2 – 15x + 25 x3
-
(3 – a)x – 2(3 – a)
-
(x + y) – 7b (y + x)
-
4a(m – n) + b2(n – m)
Остальные работают устно: По слайду вынесите общие множители:
Найдите ошибки.
2х3-3х2-х=х(2х2-3х)
2х+6=2(х+3)
8х-12у=4(2х+3у)
а6-а2=а2(а3-1)
4-2а=-2(2-а)
х3+4у2=4(х3+у2)
- Каким действием можно проверить правильность выполнения задания?
- всегда ли получаются одинаковые ответы? Почему?
-
Закрепление:
- Вашему вниманию предложены задания, которые оцениваются в разное количество баллов. Кто уверен в себе, может выбрать любые три задания и решить их самостоятельно за 7 минут. Остальные ребята работают вместе с учителем, решают самое сложное задание на доске.
-
Докажите, что значение выражения кратно 50
7 16 + 714. 4б
Ответ: 714 (72 + 1)= 714 · 50
2) Вместо звездочки поставь такой одночлен, чтобы получилось верное равенство: 6а3 – 15а2в – 24ав + ( * ) = 3а(2а2 – 5ав – 8в + 6а3в2) 2б
Ответ: 2a2b2
3) Разложи на множители: х(у – 9) + у(9 – у) – (у – 9). 4б
Ответ: (у – 9)(х – у – 1)
4) Найди корни уравнения: 18х2 = 3х. 3б
Ответ: 0; 
5) Вынеси общий множитель за скобки: (3а + 6)2. 6б
Ответ: 9(a + 2)2
6) Реши уравнение: 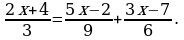 5б
5б
Ответ: 7
Проверяются выбранные задания. (Называются набранные баллы) из 18
-
Работа в парах. Задания «лото».
- У каждого на партах листочки, которые вы решаете
в парах. Если трудно, то самостоятельная работа с самопроверкой
| Кратно ли значение выражения 86 +2 15 числу 9
| Правильно ли мы вынесли общий множитель за скобки 3х-2х2+х3 = х(3-2х+ х3 ) | Вычислите наиболее рациональным способом: 153² + 153•47 |
| Решить уравнение 0,45р² + 18р =0 | Вынести общий множитель за скобки (-7а-14аb) ²
| Упростить ab(a²+ab+b²)- ab(a²-ab+b²) |
|
Карточка №1 Ф.И.
|
| Кратно ли значение выражения 144 - 74 числу 5 | Правильно ли мы вынесли общий множитель за скобки 3х-2х2+х3 = х(3-2х+ х3 )
| Вычислите наиболее рациональным способом: 168² - 168•68 |
| Решить уравнение 9у² + 0,27у = 0 | Вынести общий множитель за скобки (2x+4)2 | Упростить n(m-n)+2m(n-m)
|
|
Карточка №2 Ф.И.
|
| Кратно ли значение выражения 95 -38 числу 4 | Правильно ли мы вынесли общий множитель за скобки 12х-х2+8х3 = 4x(3-х+ 8х2 )
| Вычислите наиболее рациональным способом: 0,3³ + 0,3²•0,7 |
| Решить уравнение 2y2+8y=0
| Вынести общий множитель за скобки (-6x-9y) ² | Упростить (a+b)(a+1)-(a+b)(1-b)+(b+a)(b-a) |
|
Карточка №3 Ф.И.
|
Сам. работа (для слабых учеников)
1вариант. 2 вариант.
-
Вынеси общий множитель за скобкой :
а) 3ав – 6а а) 8ху – 16у
б) 5ха2 – 15х б) 2ав2 + 4а
в) 16у2 + 12у3 в) 18в3 – 3в5
-
Решите уравнение:
х2 – 3х = 0 2х + х2 = 0.
Самопроверка.
Критерии ошибок:
Оценка «5» - все решено верно,
Оценка «4» - одна ошибка,
Оценка «3» - две ошибки.
-
Занимательная страница. «СОФИЗМ».
Софизмом называется умозаключение, кажущиеся правильными, но ложные по сути.
Я хочу доказать вам, что 4 = 5
Равенство 4:4 = 5:5 верно.
Вынесу общий множитель за скобки 4(1: 1) = 5(1: 1)
Вычислив частное в скобках, получим 4 = 5.
Где ошибка? Ошибка: ошибка заключается в том, что нельзя было выносить множитель за
скобки в уравнении (при действии «деление»)
В то время, когда ваши мамы и папы были детьми, то есть в советские времена,
существовала такая денежная единица как рубль, которая равнялась 100 копейкам. Так вот один из софизмов говорит нам обратное.
«Один рубль не равен ста копейкам».
Доказательство:
Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. Если a=b, c=d, то ac=bd.
Применим это положение к двум очевидным равенствам
1 р.=100 коп. (*)
10р.=10·100коп. (**)
Перемножая эти равенства почленно, получим 10 р.=100000 коп.
Наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп.
таким образом, один рубль не равен ста копейкам.
Ошибка: ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.
-
Подведение итогов.
Скажите:
- для чего нужно уметь выносить множитель за скобки?
- в любом ли выражении можно вынести общий множитель?
- всегда ли получаются одинаковые ответы?
Почему?
И так вы думайте достигли ли вы цели, поставленные в начале урока?
Домашнее задание. п.28, №662,676







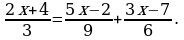 5б
5б




















