Выступление на вебинаре
Слайд1. Добрый день, уважаемые коллеги!!!
Тема моего выступления: «Формирование и оценка математической грамотности младших школьников в рамках требования ФГОС»
Цель: ознакомление педагогов с опытом работы по формированию и оценке математической грамотности младших школьников.
Слайд2. Развитие функциональной грамотности школьников определяется как одна из приоритетных целей образования.
Функционально грамотная личность – это человек, ориентирующийся в мире, человек самостоятельный, познающий и умеющий жить среди людей, обладающий определёнными
качествами, ключевыми компетенциями.
Слайд3. Содержание функциональной грамотности: грамотность в чтении и письме, в естественных науках, математическая, компьютерная, в вопросах семейной жизни, в вопросах здоровья, юридическая.
Математическая грамотность - это способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину
Учебный предмет математика предполагает формирование математических счетных навыков, ознакомление с основами геометрии;
Формирование навыка самостоятельного распознавания предметов на плоскости, практическое умения ориентироваться во времени, умение решать задачи, сюжет которых связан с жизненными ситуациями.
Главной задачей уроков математики являются интеллектуальное развитие ребенка, важной составляющей которого является словесно - логическое мышление.
Слайд4. Математическая грамотность младшего школьника как компонент функциональной грамотности трактуется как:
- понимание необходимости математических знаний для учения и повседневной жизни;
- потребность и умение применять математику в повседневных (житейских) ситуациях;
- способность различать математические объекты, устанавливать математические отношения, зависимости, сравнивать, классифицировать;
-совокупность умений.
Наша задача сегодня через содержание учебного материала, через построение урока найти то направление, которое приведет к достижению хорошего уровня функциональной математической грамотности.
Слайд5. Ориентиром для нас является стандарт начального общего образования. В нем отмечено:
«Предметные результаты освоения основной образовательной программы начального общего образования должны отражать:
-использование начальных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, а также оценке их количественных и пространственных отношений;
-приобретение начального опыта применения математических знаний для решения учебно-познавательных и учебно-практических задач» (ФГОС НОО)
Слайд6. Результаты обучения, отражающие отдельные позиции математической грамотности, могут быть конкретизированы, например:
• узнавание, называние (чтение), запись многозначного числа (в пределах миллиона);
• сравнение двух чисел (в пределах миллиона);
• ориентация в изученных величинах: единицы массы (грамм, килограмм, центнер, тонна), вместимости (литр), времени (секунда, минута, час и др.);
• соотнесение (знание соотношения) между единицами измерения однородных величин (1 тонна = 1000 кг, 1 минута = 60 секунд и др.)…
Слайд7. Результаты обучения, отражающие отдельные позиции математической грамотности, могут быть более конкретизированы, например:
• выполнение письменных вычислений, связанных с бытовыми жизненными ситуациями, на основе изученных алгоритмов (сложение/вычитание многозначных чисел, умножение/деление многозначных чисел на однозначное и двузначное число);
• выполнение (устно) арифметических действий над числами в пределах сотни и с бόльшими числами в случаях, легко сводимых к действиям в пределах ста;
• использование свойств арифметических действий для выполнения устных вычислений, необходимых в практической деятельности и повседневной жизни;
• решение текстовых задач в 1-2 действия, связанных с бытовыми жизненными ситуациями (покупка, измерение, взвешивание и др.)
Слайд8. Международные оценочные исследования функциональной грамотности: PISA, TIMSS, PIRLS
ЦЕЛЬ: оценивание не только степени усвоения учебного материала, но и способности использовать полученные навыки и знания для решения самых разных жизненных задач, то есть функциональной грамотности учащихся.
Слайд9. Проверяются три вида функциональной грамотности:
-ЧИТАТЕЛЬСКАЯ Способность к пониманию и осмыслению письменных текстов, к использованию их содержания для достижения собственных целей, развития знаний и возможностей, для активного участия в жизни общества;
-МАТЕМАТИЧЕСКАЯ способность определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину.
-ЕСТЕСТВЕННО - НАУЧНАЯ Способность использовать естественнонаучные знания для отбора в реальных жизненных ситуациях тех проблем, которые могут, исследованы и решены с помощью научных методов, основанных на наблюдениях и экспериментах, необходимых для понимания окружающего мира и тех изменений, которые вносит в него деятельность человека, а также для принятия соответствующих решений.
TIMSS — как в начальной и средней школе знают математику и естественные науки
Что проверяют. Основная цель исследования — сравнить между собой качество математического и естественнонаучного образования в начальной и средней школе.
Кто участвует. Ученики 4-х и 8-х классов.
Когда проходит. Каждые четыре года. Такая схема позволяет отслеживать, какие изменения происходят в образовании при переходе из начальной в основную школу и как они влияют на качество образования.
Как в TIMSS показывают себя школьники из России. Результаты у российских школьников достаточно высокие. В последнем исследовании 2015 года ученики 4-х классов заняли 7-е место по математике.
Слайд10. Задание для 4-х классов по математике:
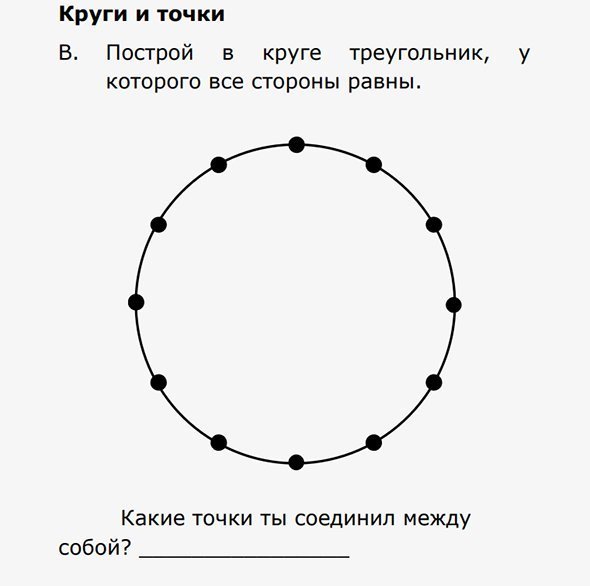
Комментарий эксперта к заданию: «Проверяется умение вписать равносторонний треугольник в окружность, разделённую на равные части. Требовалось не только увидеть, что окружность разделена на равные части, но и сообразить, что надо соединять отрезками каждую четвёртую точку, чтобы построить равносторонний треугольник, и описать способ соединения точек. Подобных заданий нет в учебниках. Практически все российские четвероклассники пытались решить это задание. Большинство справились с ним (верно выполнили его полностью 68%, верно построили, но не описали — 7%)».
Слайд11. Математическая функциональная грамотность – это комплекс трех компонентов:
-ученик понимает необходимость математических знаний, чтобы решать учебные и жизненные задачи, умеет оценивать учебные ситуации, которые требуют математических знаний;
-школьник способен устанавливать математические отношения и зависимости, работать с математической информацией: применять умственные операции, математические методы;
-ученик владеет математическим языком, применяет его, чтобы решить математические задачи, построить математические суждения, работать с математическими фактами.
Слайд12. Первый компонент
Чтобы его сформировать, нужно найти ответ на вопрос ученика: «А зачем мне эта математика нужна?». Поэтому на уроке важный момент – проанализировать ситуацию, которая стимулирует потребность и желание изучать математику.
| Пример |
| Учитель показывает изображение автомобиля и предлагает четвероклассникам продолжить предложение: «В Австралии в 2017 году прошла гонка, в которой участвовали только автомобили на…( на солнечных батареях) Какие это автомобили?». Дети высказывают предположения: «Автомобили на воздушных подушках, электричестве, газе, солнечных батареях?». После этого учитель демонстрирует текст, в котором содержится ответ на этот вопрос: «Благодаря электричеству, подаренному солнцем, можно ежедневно проезжать 30 километров. Некоторые авто способны разгоняться до 89 км/ч. Именно этот автомобиль победил в гонке в 2017 году. Он сконструирован сотрудниками голландской компании. Солнечная батарея авто весит 135 кг, ее площадь 2 м2 64 дм2». Учитель продолжает диалог с детьми: «Какие величины вы встретили в этом тексте? Надо ли учить математику, чтобы читать и понимать информацию о современных достижениях науки и техники?». Ответы детей на эти вопросы позволят показать необходимость получать и применять математические знания. |
Слайд13. Примеры заданий, чтобы сформировать первый компонент математической функциональной грамотности
1.
1. Сколько сдачи ты получишь с каждой покупки, если у тебя купюра 50 руб.,а ты купишь: один йогурт (32 руб. )? одно мороженое (26 руб. )?
2. Дима заметил, что упаковка сока стоила 36 руб. Через некоторое время его цену снизили на 8 руб. По какой цене стали продавать сок?
3.Тульские пряники вошли в бортовое меню авиаперевозчика «Аэрофлот». Для этого фабрика будет производить более 7 млн пряников в год. Вычисли, сколько пряников кондитеры выпекут за полгода, за один месяц (30 дней), за один день, если за год на фабрике выпекут 7 200 000 пряников?
4.Москва – Владивосток – это самый протяженный железнодорожный пассажирский маршрут в мире. За 144 часа вы преодолеваете путь длиной в 9288 км. Выполни деление с остатком: вычисли скорость движения поезда по этому маршруту.
5.Определи время по часам. Запиши результаты по образцу.
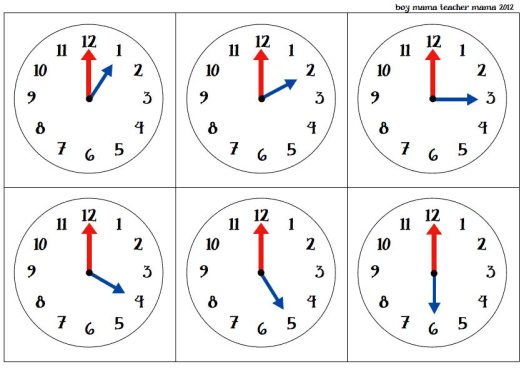
Использование таких задач расширяет математический кругозор младших школьников, способствует математическому развитию и повышает качество математической подготовленности.
Слайд14-17. Второй компонент
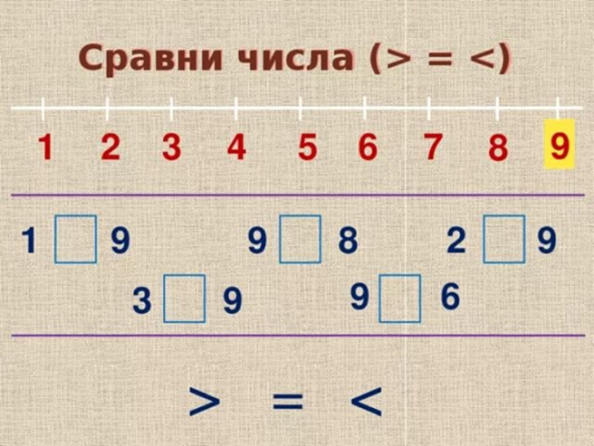
Чтобы его сформировать, давайте детям на уроках задания: сравнить предметы (фигуры) по их форме и размерам, сравнить числа;
Слайд18. упорядочить данное множество чисел, сравнить разные способы вычисления, выбрать наиболее удобный; проанализировать структуру числового выражения, чтобы определить порядок выполнения арифметических действий.
Слайд19. Попросите учеников сравнить значения однородных величин (длина, площадь, периметр, масса, время, скорость, цена, стоимость), упорядочить заданные значения величин; установить зависимости между данными и искомыми величинами при решении разнообразных учебных задач; моделировать зависимости, которые содержатся в тексте задачи; сравнить и обобщить информацию, которая представлена в таблицах, на диаграммах;
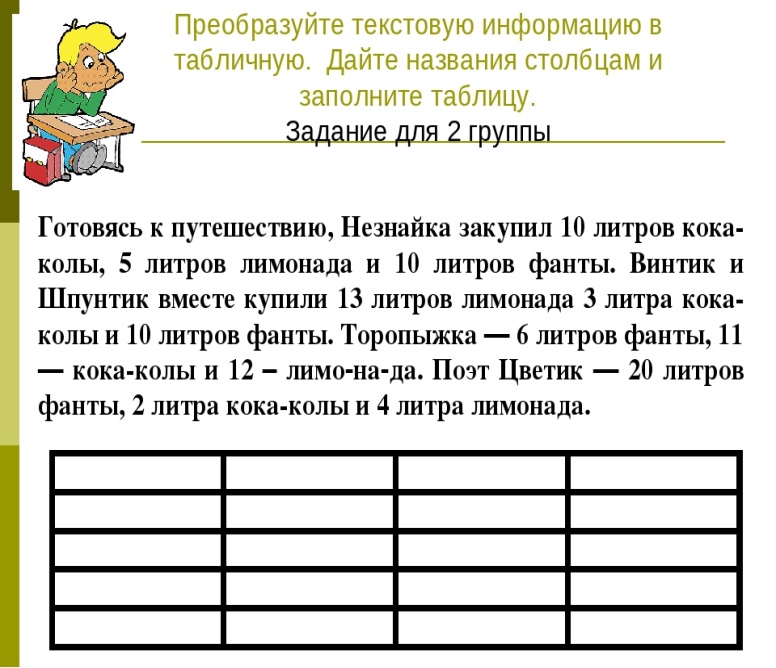
Слайд20. перевести информацию из текстовой формы в табличную.
Чтобы успешно выполнить задания, у детей должны быть сформированы читательская грамотность и смысловое чтение текстов: информационно-содержательного, инструктивного, справочного, текста-обращения, текстовой задачи.
Примеры заданий, чтобы сформировать второй компонент математической функциональной грамотности.
2. Компонент.


Слайд21. Третий компонент
Чтобы сформировать третий компонент математической функциональной грамотности, применяйте задания: понять и применить математическую символику и терминологию, построить математические суждения (рассуждения). Полезно побуждать детей высказываться в ситуациях спора, дискуссии, которые вызваны противоречием.
| 1. Пример |
| В детский сад привезли 20 кг яблок и 8 пакетов винограда. На сколько килограммов больше привезли яблок, чем винограда? Учитель предлагает ответить на вопросы: Кто готов выполнить задание и знает, что получит правильный результат? Можно ли решить эту задачу? Почему нет? да? Все ли условия есть для ее решения? Что нам необходимо, чтобы получить требуемый результат? |
3 .Хочу предложить вам Комплекс заданий способствующих развитию
математической грамотности обучающихся.
Слайд22. Задания для развития математической речи при работе с числовыми упражнениями:
1)
3) Прочитайте словесные формулировки числовых выражений. Запишите их с помощью цифр и знаков действий и найдите их значения.
К четырём прибавить два, а затем из суммы вычесть два.
К девяти прибавить один, а затем из суммы вычесть один.
Из семи вычесть четыре, а затем к разности прибавить четыре.
Из шести вычесть три, а затем к разности прибавить шесть.
4)Игра «Сюрпризный конверт»
11-9
12-8
16-7
8+7
5+6
9+4
Учащимся даётся задание записать данные числовые выражения в тетрадь и найти их значения. Затем из «сюрпризного конверта» дети достают карточку со словесными формулировками данных числовых выражений. Им необходимо отметить знаком «+» те формулировки, которые соответствуют данным числовым выражениям:
Из одиннадцати вычесть девять.
Сумма чисел восьми и семи.
Первое слагаемое двенадцать второе слагаемое восемь.
Число пять увеличить на шесть.
Число шестнадцать уменьшить на семь.
Четыре увеличить на девять.
7) Игра «Верно ли что?» Ребятам предлагается словесная формулировка высказывания, которую нужно перевести в знаковую форму, затем определить ложность данных высказываний.
Двенадцать больше трёх на девять;
с восьми часов утра до пятнадцати часов того же дня прошло шесть часов;
сумма семи и восьми равна шестнадцать;
шестнадцать меньше семи.
5. На знание математических терминов, использовали следующий игровой момент:
1. Учитель или ученик называет часть слова (слага...) и бросает мяч. Другой ученик должен поймать мяч и дополнить слово (... емое).
6. Противоположные слова
Назвать слова, противоположные по значению.
· Прямая -
· Равенство -
· Четное -
· Много -
· Сложение -
7.Опрокинутые слова
Ученикам предлагался комплект слов, в которых буквы перепутаны местами. Нужно восстановить типичный порядок слов.
Скажем:
· УМАСМ - СУММА.
· АЕМОСЛАГЕ (слагаемое).
· ЧИТАВЫЕМОЕ (вычитаемое).
· КРАТВАД (квадрат).
· УГОТЬРЕНИК (треугольник).
· РЕЗОТОК (отрезок).
8.На правильное применение математических терминов предлагались задания:
Озаглавьте каждый столбец
|
|
|
|
|
| 23 4 1 8 8 1  00 00 96 55 | 
| Миллиметр Сантиметр Дециметр Метр Километр | Сложение Вычитание |
9. «Терминологическая викторина»:
1. Линия, которую невозможно свернуть? (прямая)
2. Оценка плохого ученика? (два)
3. Часть прямой, но не луч. (отрезок)
4. Ребус: в букве О число 7. (восемь)
5. Единица измерения длины, равная 100 см (метр)
6. Прямоугольник, у которого все стороны равны. (квадрат)
7. В треугольнике их 3. (углы)
8. Инструмент школьника для измерения длины. (линейка)
9. Форма Солнца, часов …. (круг)
10. Результат сложения. (сумма)
Работая над математической грамотностью детей приходится задумываться о том, как и в какой форме донести до наших детей учебный материал.
Этот вопрос волнует не только меня, но и всех учителей начальных классов. Абсолютного и окончательного ответа на этот вопрос мы, наверное, не получим никогда, но это вовсе не означает, что поиски следует прекратить.
Известный математик Джордж Пойа говорил: «Что значит владение математикой? Это есть умение решать задачи, причем не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности».
Создание на занятиях ситуаций активного поиска, предоставление возможности сделать собственное «открытие», знакомство с оригинальными путями рассуждений, овладение элементарными навыками исследовательской деятельности позволят обучающимся реализовать свои возможности, развить способности самостоятельной познавательной деятельности, приобрести уверенность в своих силах.
Таким образом, задачи по формированию функциональной грамотности, в частности, математической грамотности обучающихся, возможно реализовать при условии оптимального сочетания учебного содержания базового уровня образования и дополнительных курсов, направленных на совершенствование прикладных математических умений, использующихся в различных жизненных ситуациях.
Таким образом, Систематическое использование на уроках математики специальных задач и заданий, формирует и развивает функциональную грамотность младших школьников, позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.













 8
8
 00
00










