Выступление по теме "Приёмы обучения в инклюзивном классе (на примере математики)"

Приёмы обучения в инклюзивном классе

(на примере математики)

Лев Семёнович Выготский указывал на необходимость создания такой системы обучения, в которой ребёнок с ограниченными возможностями не исключался бы из общества детей с нормальным развитием.

Инклюзивное (французское слово inclusif — включающий в себя, от латинского include — заключаю, включаю) или включённое образование — термин, используемый для описания процесса обучения детей с особыми потребностями в общеобразовательных (массовых) школах.

До недавнего времени, обучение детей с ОВЗ носило исключительно индивидуальный характер. Группы данных детей курировались специальными педагогами в специальных учебных организациях.

В настоящее время каждый имеет право решать, где и как ему учиться. Образование стало доступным для всех.

Инклюзивное образование играет важную роль в саморазвитии каждого ребенка. Дети с ОВЗ приобретают навыки саморазвития, самосовершенствования, укрепляют своё положение в социуме.

Одна из главных проблем, которые приходится решать учителю на уроке — это работа со слабоуспевающими учащимися. Слабоуспевающие — дети, плохо подготовленные к учебному материалу, имеющие низкий уровень интеллектуальных способностей. Работать с такими детьми сложно во многом из-за того, что у таких детей нет элементарного интереса к предмету, отсутствует стимул хорошо учиться, а давление со стороны учителей и родителей лишь усугубляет ситуацию.

Как обучить всех: и тех, кто учится с интересом, и тех, у кого его нет?

В практике можно применять большое количество разнообразных приёмов. Заслуживает внимания такой приём, как «алгоритмическая деятельность». Этот приём НЕ приводит к стандартизации мышления, не подавляет творчество, но даёт возможность усвоить обязательный уровень знаний наиболее слабым обучающимся. Следует выделить 3 этапа работы с этим приёмом при обучении решению задач:

1. схема к задаче, включающая условие и вопрос задачи;

2. составление плана решения (что главное? Что от чего зависит? Как можно найти ответ на вопрос задачи?);

3. анализ решения задачи, т.е. сам ученик рассказывает как решал задачу, почему в такой последовательности, почему выбрал данное арифметическое действие сначала, потом …

Данный навык учитель начинает формировать через «рассказ», «объяснение» на конкретной задаче. Для закрепления и отработки алгоритма решения задач идёт в практической работе на уроке. При этом я использую разные формы работы: фронтальный — всем классом проговаривая каждый этап, групповой — здесь нужно рационально организовать, объединить детей в группу (когда более «сильный» ученик показывает дополнительный пример более слабым обучающимся), индивидуальный — это наиболее результативная форма работы. Для того, чтобы выявить тех учащихся, которые что-то не поняли, провожу небольшие самостоятельные работы, и оказываю им оперативную помощь.

Как один из эффективных приёмов считаю использование «памяток», в которых записаны правила и образцы выполнения заданий (всем хорошо известен факт, что у слабоуспевающих детей есть проблема с запоминанием. Здесь учителю поможет работа с чертежами, рисунками, схемами, таблицами. Всё это способствует развитию зрительной памяти).

Составлена памятка для каждого слабого обучающегося, где указана приёмы работы с учебным материалом (с учебником математики). Это необходимо для того, чтобы ребёнок мог самостоятельно работать или при дистанционном обучении.

Запомни и действуй:

1. Прочитай содержание параграфа или отдельного пункта;

2. Выдели новые, непонятные слова и выражения. Выясни их значение через разные источники;

3. Сформулируй себе вопросы по теме и ответь на них;

4. Выпиши основные понятия;

5. Внимательно разбери схему, таблицу, чертёж, рисунок, …;

6. Попробуй составить схему, используя свои обозначения;

7. Прочитай ещё раз, предварительно поставив цель «Запомнить»;

8. Ответь на вопросы, если они есть в конце параграфа учебника.

Отметила, что большой интерес вызывает у учащихся решение задач жизненного характера. Практико-ориентированные задачи:

1. 1. Необходимо добраться от Переславля-Залесского до Ярославля. Расстояние - 120 км, скорость - 40 км/ч. Найти время в пути.

1. Какова будет стоимость вегетарианского борща, если 0,5 кг капусты стоит 85 руб., 0,5 кг картошки– 70 руб., 0,2 кг свёклы – 45 руб., 0,2 лука – 40руб., 0,4 кг моркови – 50 руб.

1. Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 8 дней. В одной упаковке 10 таблеток лекарства по 0,25 г. Какого наименьшего количества упаковок хватит на весь курс лечения?

Ещё один момент, ньюанс, который следует учитывать в работе с такими детьми — это рациональное распределение учебного материала. Он должен даваться в определённой последовательности и степень трудности нарастает постепенно, по мере усвоения фактического материала.

В работе со слабоуспевающими обучающимися следует отмечать и поощрять малейшие удачи, даже незначительные сдвиги — это вселяет уверенность в ребёнка.

Учитель всегда помнит — в центре внимания — ученик! Я никогда не сравниваю детей между собой, но обязательно показываю достижения ребёнка по сравнению с его предварительным (вчерашним) достижением.

Использую систему разноуровневых домашних заданий: дозировка, творческий характер, соизмерение объёма домашнего задания и сложность с возможностями каждого ученика. Например, слабоуспевающий решает задачу на движение, а сильные ученики — самостоятельно придумать аналогичную задачу. Или решать уравнения «по аналогии» с примерами и составить собственные уравнения.

Подготовке к ГВЭ по математике

Особое значение уделяю подготвке к ГВЭ по математике. Цель: мотивация и успешное прохождение экзамена.

На консультациях я неоднократно использую бланки ответов, анализируем вместе с ребятами ошибки заполнения, особенности записи ответов. Тем не менее, обучающиеся не всегда обращают внимание на образцы цифр и букв, некорректно записывают ответы (используют в записи единицы измерения величин, вместо запятой – точку, разделяют точкой с запятой ответы в заданиях на соответствие).

Систематически провожу внутришкольный мониторинг, который позволяет проверить уровень усвоения материала и определить пробелы в знаниях. Полученные результаты определяют индивидуальную и дифференцированную работу с обучающимися. Мониторинг и диагностика проводится на основе экзаменационных материалов.

По результатам мониторинга можно определить набор тем, хорошо усвоенных и, так сказать, западающих для всего класса и для каждого обучающегося в отдельности.

Организация повторения

Для хорошей подготовки к экзамену необходимо целенаправленное повторение разделов курса математики 5–6-х классов, алгебры и геометрии 7–9-х классов и и систематический мониторинг продвижения отдельных обучающихся по ликвидации пробелов за основную школу.

На каждом уроке включаю материал на повторение через систему упражнений составленных на основе материалов ГВЭ.

Важным условием успешной подготовки к экзаменам является тщательное отслеживание результатов обучающихся по всем темам и своевременная коррекция уровня усвоения учебного материала.

Для организации разного уровня обучения и обобщающего повторения обучающиеся с ОВЗ разбиваются на 3 группы.

1 группа - группа «риска» - обучающиеся, которые должны справиться с заданиями базового уровня и получить на экзамене «3». Необходимо учесть, чтобы обучающиеся первой группы уверенно выполняли 3 задания.

Обучающиеся:

1) должны выучить всю теорию;

2) научиться решать все типы заданий базового уровня;

3) на контрольных работах, тестах не списывать.

2 группа - обучающиеся, которые должны справиться с заданиями базового уровня и более сложными заданиями, то есть применять ЗУН в измененной ситуации. Обучающиеся этой группы должны выполнять от 4 до 7 заданий.

А для этого они:

1) должны выучить всю теорию;

2) научиться решать все типы заданий любой темы разными способами;

3) уметь объяснять, почему так решаешь;

4) уметь решать задачи на уравнения, проценты.

3 группа - обучающиеся, которые поставили перед собой цель получить высокий балл, которые умеют решать задания самой высокой сложности, то есть применять ЗУН в новой ситуации. (8-10 заданий).

Обучающиеся этой группы:

1) должны выучить всю теорию;

2) научиться решать все типы заданий любой темы разными способами;

3) уметь объяснять, почему так решаешь;

4) знать теорию геометрии;

5) знать материал по теории вероятности и статистике.

Я провожу консультацию раз в неделю для всех обучающихся. А по пятницам консультирую обучающихся заинтересованных в высоком балле за экзамен. Отвечаю на вопросы, вместе анализируем их ошибки, разбираем типы заданий. Рекомендовала всем завести тетрадь для подготовки к экзамену, в которых последние несколько страниц отвести под формулы и свойства, записывая их здесь по мере решения задач; рекомендую рассмотреть видеоуроки по различным темам, которые вызвали затруднение, интерактивные тесты. Непременное условие хорошей результативности экзамена – это стремление самого обучающегося к успеху.

Карта мониторинга

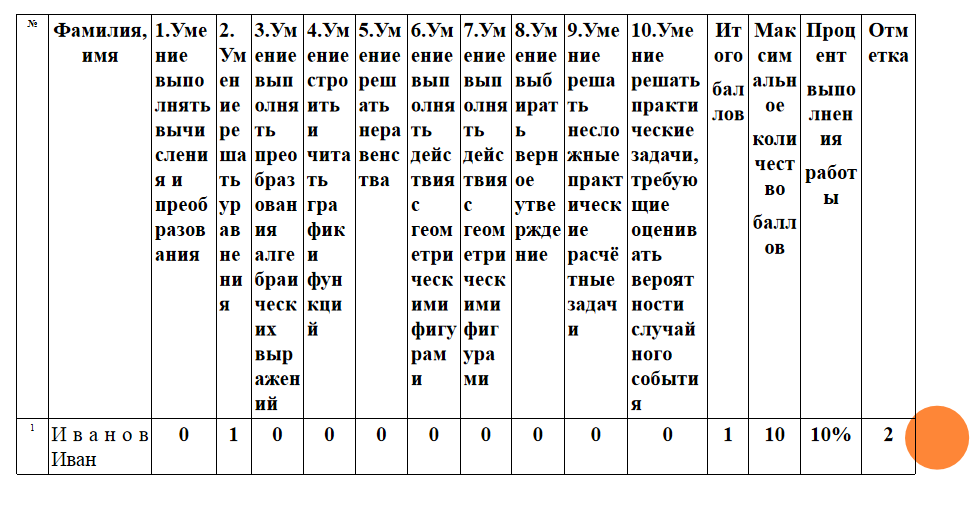
 Решение задач ГВЭ на уроках и консультациях, при этом можно начинать с заданий обязательного уровня, затем постепенно их усложнять, учитывая индивидуальные особенности обучающегося. Предлагаю домашнее задание: тренировочные работы. Для этого я использую дидактические материалы, где они знакомятся с разнообразием заданий, проверяют уровень своих знаний, в случае затруднения просматривают правильное решение или выносят вопросы на консультацию.

- обучаю приёму «спирального движения» по тесту, отметить то, что кажется простым, понятным и лёгким, выполнить задания, которые можно выполнить без раздумий.

- обучаю обучающихся внимательному и осмысленному прочтению текстов задач, в том числе и геометрических, а также выбору оптимальной стратегии их решения.

-проверяю полученный результат решения.

Важным условием успешной подготовки к экзаменам является тщательное отслеживание результатов обучающихся по всем темам и своевременная коррекция уровня усвоения учебного материала.

Интернет-ресурсы при подготовке к ГВЭ

1. СДАМ ГИА: РЕШУ ГВЭ (https://math9-gve.sdamgia.ru)

2. Инфоурок (https://infourok.ru)

3. Мультиурок (https://multiurok.ru)

4. ФИПИ (https://fipi.ru)

Работа учителя (как должна строится):

• каждый урок - продолжение предыдущего;

• многократное повторение основного материала;

• учёт низкой скорости чтения, счета и письма;

• для лучшего запоминания чаще предлагать однотипные задания;

• задания, идущие от простого к сложному;

• постоянно поддерживать у ребёнка уверенность в своих силах;

• нужно дать некоторое время для обдумывания, если ответ не верный, попросить ответить через некоторое время;

• не отвлекать во время выполнения задания, на какие – либо уточнения, дополнения;

• использовать зрительные опоры, схемы, таблицы.