Взаимное расположение двух окружностей

Взаимное расположение двух окружностей

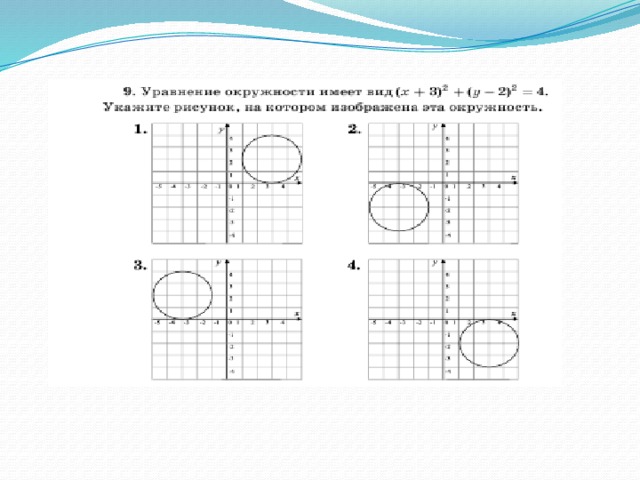
Уравнение окружности и прямой

• Уравнение окружности с центром в точке и радиусом r
• Уравнение окружности, центром которой является начало координат
• Уравнения, которые задают произвольную прямую

• - угловой коэффициент прямой.

Возможные случаи взаимного расположения окружностей

1. Центры окружностей совпадают

• Такие окружности называются  концентрическими . Если радиусы окружностей не равны, то такие окружности образуют  кольцо.  Если радиусы окружностей равны, то окружности совпадают

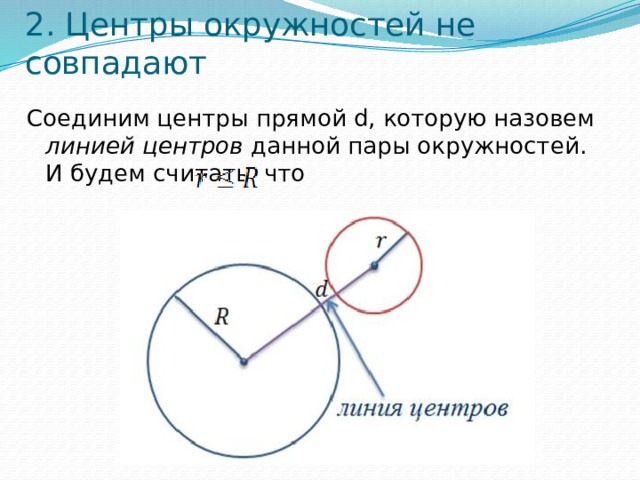
2. Центры окружностей не совпадают

Соединим центры прямой d, которую назовем линией центров данной пары окружностей. И будем считать, что

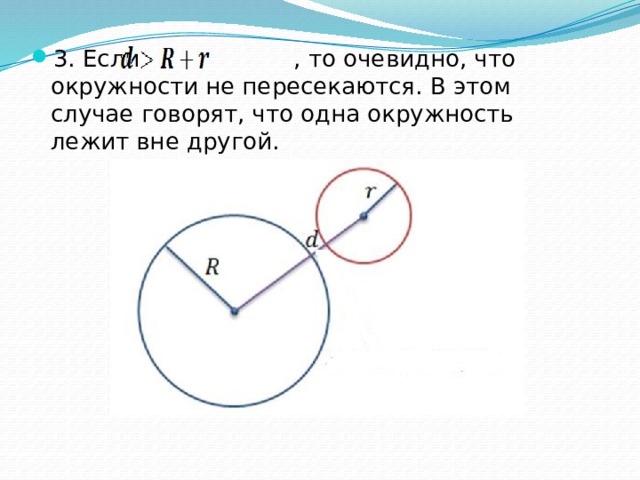
• 3. Если , то очевидно, что окружности не пересекаются. В этом случае говорят, что одна окружность лежит вне другой.

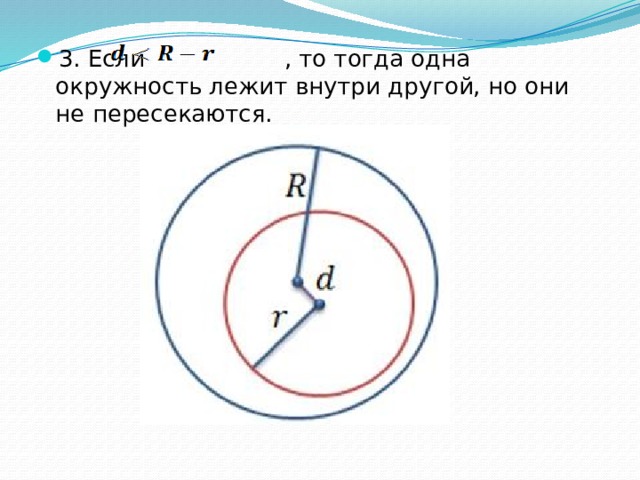
• 3. Если , то тогда одна окружность лежит внутри другой, но они не пересекаются.

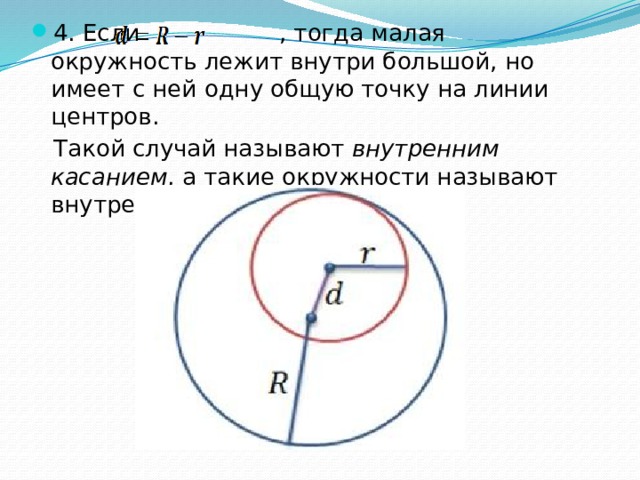
• 4. Если , тогда малая окружность лежит внутри большой, но имеет с ней одну общую точку на линии центров.

Такой случай называют  внутренним касанием , а такие окружности называют внутренне касающимися.

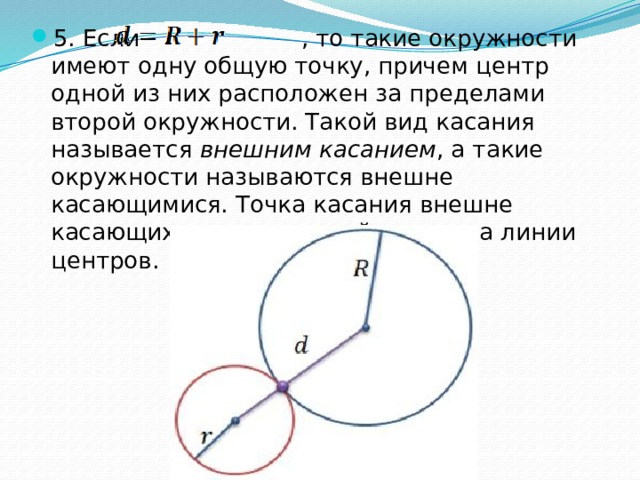
• 5. Если , то такие окружности имеют одну общую точку, причем центр одной из них расположен за пределами второй окружности. Такой вид касания называется  внешним касанием , а такие окружности называются внешне касающимися. Точка касания внешне касающихся окружностей лежит на линии центров.

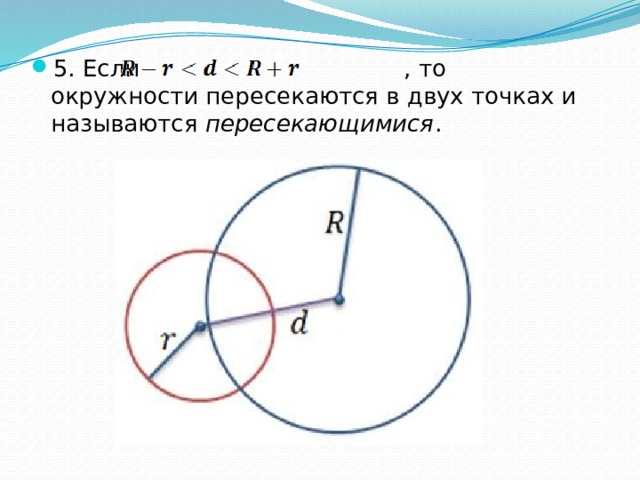
• 5. Если , то окружности пересекаются в двух точках и называются пересекающимися .

Задача 1

Окружности касаются внешним образом. Радиус меньшей окружности равен 3 см. радиус большей- 5 см. Чему равно расстояние между центрами?

Задача 2

Окружности касаются внутренним образом. Радиус меньшей окружности 3 см. Радиус большей окружности- 5 см. Чему равно расстояние между центрами окружностей?

Задача 3

Окружности касаются внутренним образом. Расстояние между центрами окружностей 2,5 см. Чему равны радиусы окружностей?