Взаимное расположение окружностей

Взаимное расположение окружностей

Выполнил

Ученик 9 “В” класса

Лось Вадим

Признаки

• Взаимное расположение окружностей можно различать по внешнему признаку (касающиеся, пересекающиеся, непересекающиеся) или по внутреннему признаку (взаимное расположение центров окружностей относительно общей касательной, общей хорды и т.д.).

Расположение центров окружностей относительно общей касательной

• В условии задач этого типа фигурируют две окружности, касающиеся одной прямой, но не указано расположение центров этих окружностей относительно этой прямой. Соответственно эта прямая является внутренней или внешней касательной для этих окружностей.

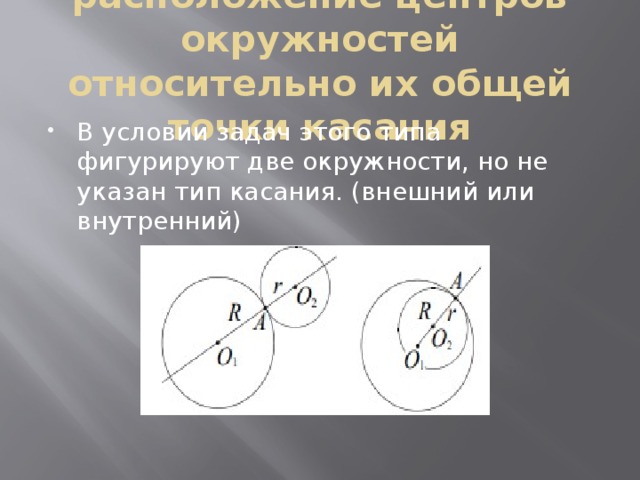
расположение центров окружностей относительно их общей точки касания

• В условии задач этого типа фигурируют две окружности, но не указан тип касания. (внешний или внутренний)

При решении подобных задач полезно вспомнить следующие факты.

• При любом способе касания точка касания и центры окружностей лежат на одной прямой.
• При внешнем касании центры окружностей расположены на линии центров по разные стороны от точки касания, при внутреннем – по одну сторону.
• Расстояние между центрами касающихся окружностей радиусов R и r (R ≥ r )равно R + r при внешнем касании и R − r при внутреннем.

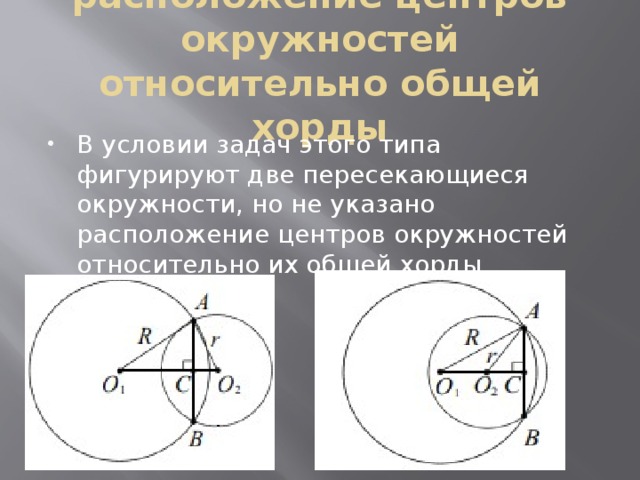
расположение центров окружностей относительно общей хорды

• В условии задач этого типа фигурируют две пересекающиеся окружности, но не указано расположение центров окружностей относительно их общей хорды.

При решении подобных задач полезно вспомнить следующие факты.

• Пересекающиеся окружности в точках А и В имеют общую хорду АВ.
• Общая хорда перпендикулярна линии центров и делится ею пополам

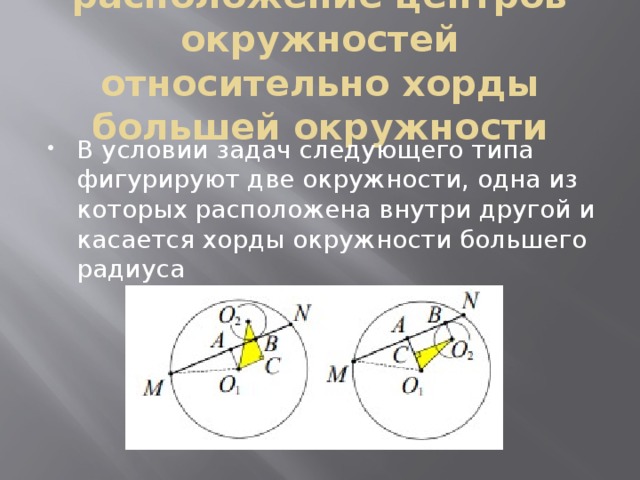
расположение центров окружностей относительно хорды большей окружности

• В условии задач следующего типа фигурируют две окружности, одна из которых расположена внутри другой и касается хорды окружности большего радиуса

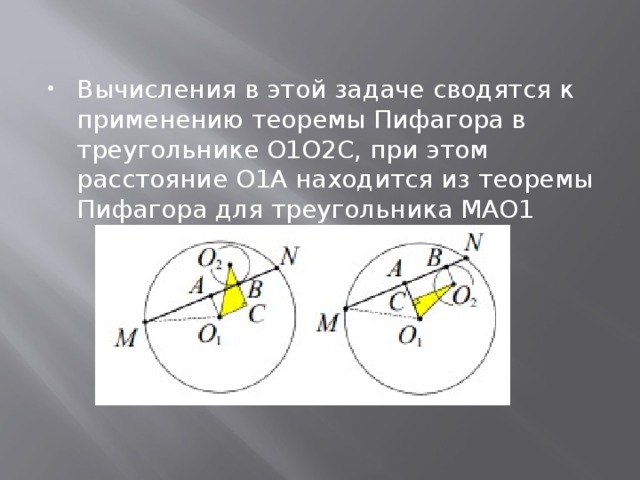
• Вычисления в этой задаче сводятся к применению теоремы Пифагора в треугольнике О1О2С, при этом расстояние О1А находится из теоремы Пифагора для треугольника МАО1

r и a r + R. Найти расстояние между точками касания. " width="640"

Задача №1

• Прямая касается окружностей радиусов R и r. Известно, что расстояние между их центрами равно a, причем R r и a r + R. Найти расстояние между точками касания.

Решение

Пусть О1 – центр окружности радиуса R, О2 – центр окружности радиуса r, A1A2 и B1B2 – внешняя и внутренняя касательные соответственно. Из центра меньшей окружности опустим перпендикуляры O2K1 и O2K2 на радиус O1A1 и продолжение радиуса O1B1 соответственно.

Рассмотрим прямоугольные треугольники O1K1O2 (гипотенуза O1 O2 = a , катет O1 K1 = R - r ) и O1K2O2 (гипотенуза O1 O2 = a катет O1 K2 = R +r). Из теоремы Пифагора для этих треугольников получим:

Задача №2

• Окружности радиусов 2 и 4 касаются в точке B. Через точку B проведена прямая, пересекающая второй раз меньшую окружность в точке A, а большую – в точке C. Известно, что AC = 3√2 . Найти BC

Решение

Поскольку в условии не сказано о типе касания окружностей (внешнее или внутреннее), то рассмотрим два случая.

• Если окружности касаются внешним образом, то проведем через точку B общую касательную KK1 (она перпендикулярна линии центров). Так как треугольники AO2B и COB1 равнобедренные и ∠ O2BA = ∠ O1BC , то они подобны по первому признаку подобия. Для подобных треугольников AO2B и O1BC можем записать

2. Окружности касаются внутренним образом. В этом случае при исходных числовых данных задача не имеет решения

Источники

• http:// alexlarin.net/ege/2013/c42013.pdf
• http://zadachi.mccme.ru/2012/#& page4
• http:// www.problems.ru/view_problem_details_new.php?id=52819
• http:// edu.sernam.ru/book_el_math.php?id=174

Спасибо за внимание!