Взаимосвязь математики и музыки. Дроби в музыке.

Разработка.

Урок- исследование «Математика и музыка» ( 8 класс)

Учитель: Мигинская Людмила Михайловна

Цели:

1. Провести исследование связи между музыкой и математикой, рассмотреть несколько музыкальных произведений, взятых из разных направлений.

2. Доказать тесную взаимосвязь математики и музыки.

3. Воспитывать эстетический вкус. Прививать любовь математике, посредством связи с музыкой.

Наглядность и оборудование.

1. Портреты Пифагора, Эйнштейна и Свиридова.

2. Песня «Время, вперёд!»

3. Волшебный квадрат Пифагора.

4. Песни о математике и о школе.

5. Таблица с нотами и долями.

1. Вводная беседа

Объявление цели и задач урока.

Учитель. О связи музыки и математики уже много веков назад задумывались многие учёные. Например:

-Пифагор именно в музыке нашёл прямое доказательство своему знаменитому тезису «Всё есть число». Об этом сегодня и будет разговор (демонстрация портрета Пифагора)

-Эйнштейн сказал: « Настоящая наука и настоящая музыка требуют однородного мышления» (демонстрация портрета Эйнштейна)

Об этом можно привести ещё много высказывание знаменитых математиков.

Задача нашего урока доказать это, начнём с прослушивания произведения. Свиридов Георгий Васильевич - композитор и пианист он написал произведение, которое называется «Время, вперёд!» Послушайте и постарайтесь представить, что рисует эта музыка, о чём она, какое воздействие оказывает на слушателя (прослушивание музыки).

- Как будто ракета взлетает, новые достижения, движение вперёд!

- Развитие каких-то событий (важных)

- Мелодия взлетает всё выше и выше.

Какое это произведение мелодичное или ритмичное? ( ритмичная)

Что же такое ритм? Ритм- идёт отстукивание, чередование длительности звуков или выполняется какой-то порядок.

А возможно ли это без участия математики? (Нет)

Попробуем это доказать. Когда мы произносим слово ритм, наши мысли обращаются к музыке, и это верно, ведь ритм один из важнейших элементов музыки, но ритм можно обнаружить и среди чисел.

(Демонстрируется порядок закономерности на примере волшебного

квадрата четных чисел Пифагора)

Мы уже сказали, что ритм - это чередование длительности звуков (слабых и сильных)

Демонстрируется таблица №1

Вы видите, что дроби широко используются в музыке. Сразу понятно -насколько один звук должен быть короче или длиннее другого.

Давайте, используя таблицу, решим несколько примеров

(Таблица 2)

Ответы: І.сравнить

1. 3) ¼ больше 1/8

2) 4) 1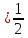

І І.Проверить равенства:

4)

Но этого недостаточно для написания (создания) музыки. Чтобы записать слова используют буквы, а музыку- ноты.

1. Сколько всего нот? (7)

Где ещё в жизни в природе встречается это число?
(Семь цветов радуги; Семь чудес света; Семь морей( так считали в древности); пословицы)

Учащиеся приводят свои примеры

1. Параллелограмм- есть такое понятие в музыке. Сколько пар параллельных прямых в слове НОТЫ (3).

Приведите примеры изученных в 8 классе в фигур, у которых есть пары параллельных отрезков.

Параллели можно обнаружить и в самом звучании музыки:

*звучит песня о математике*

Сколько здесь голосов? (мужских и женских)

Наблюдается здесь параллельность?

Одновременное (параллельное) звучание двух голосов (женских выше мужской ниже, но красиво, да?)

Параллельного могут звучать голоса, музыкальное сопровождение

Звучания голосов в хоре

Музыку можно изобразить с помощью нот и математического графика (изображение графиков)

Давайте проведем музыкальное математическую викторину, которую подготовили ученики.

Рассмотрим понятие противоположность.

Весь мир состоит из противоположностей:

В математике: плюс – минус, прямая – кривая, чётное – нечетное число, больше – меньше, сложение – вычитание. (Придумайте ещё примеры противоположностей)

В музыке:

Быстро – медленно, громко – тихо, одногласие – многогласие, высокое – низкое. (Придумать ещё примеры)

Заключение. Подведем итог.

Наш урок - исследование продемонстрировал тесную связь музыки и математики, в них есть много общего. Общие понятия, какие? (Параллельность, противоположность, симметрия построения). Общие черты в использовании специальных символов(каких?). Занимаясь музыкой человек тренирует свои математические способности.

Цель урока достигнута, задачи выполнены.

Вывод: Математика может развиваться без музыки, ф музыкальное искусство подчиняется многим законам математики и не может существовать без неё. Музыка есть таинственная арифметика души: она вычисляет сама того не осознавая.

А сейчас, послушаем песни, посвященные математике.