

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 14.03.2025 16:34

Брусницына Светлана Алексеевна
учитель математики
58 лет
Местоположение
Россия, Ростов
Специализация
Зачетная работа по теме: "Тригонометрические уравнения" 10 класс
Категория:
Алгебра
26.10.2019 15:18


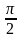 – х ) – 2 = 0 б) Найдите все корни этого уравнения, принадлежащие отрезку [−5π; −7π/2 ]
– х ) – 2 = 0 б) Найдите все корни этого уравнения, принадлежащие отрезку [−5π; −7π/2 ]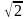 sin³ x−
sin³ x− 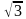 cos² x − 4 sin x + 4
cos² x − 4 sin x + 4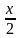 - cos²
- cos² 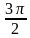 + 2х ) = cos x. а) Решите уравнение. б) Укажите корни уравнения, принадлежащие отрезку [5π/2; 4π ]
+ 2х ) = cos x. а) Решите уравнение. б) Укажите корни уравнения, принадлежащие отрезку [5π/2; 4π ]









