Зачет №1.
Начальные геометрические сведения.
1 вариант
Установите верно или неверно высказывание.
-
Вертикальные углы равны.
-
Если угол острый, то смежный с ним угол также является острым.
-
Сумма смежных углов равна 180°.
-
Если угол равен 45°, то вертикальный с ним угол равен 45°.
-
Любые две прямые имеют ровно одну общую точку.
-
Через любую точку проходит более одной прямой.
-
Если угол равен 60°, то смежный с ним равен 120°.
-
Сумма вертикальных углов равна 180°
-
Через любые две точки можно провести прямую.
-
Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой.
-
Смежные углы равны.
-
Если угол равен 108°, то вертикальный с ним равен 72°.
-
Если угол равен 47°, то смежный с ним равен 143°.
-
Если две прямые перпендикулярны третьей прямой, то эти две прямые не пересекаются.
-
Через любую точку проходит ровно одна прямая.
-
Если угол равен 120°, то смежный с ним равен 120°
-
Всегда один из двух смежных углов острый, а другой тупой.
-
Через любые две точки можно провести прямую, и притом только одну.
-
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
-
Единицей измерения угла является миллиметр, сантиметр, дециметра.
-
Каждая сторона развернутого угла является продолжением другой стороны.
-
Градусная мера развернутого угла менее 1800.
-
Луч, исходящий из вершины угла и делящий его на две части, называется биссектрисой угла.
-
Угол называется прямым, если он равен 900.
-
Угол называется острым, если он больше 900.
-
Угол называется тупым, если он меньше 900.
-
Простейший прибор для измерения углов на местности является астролябия.
-
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются вертикальными.
-
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
-
Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
-
Равные отрезки имеют разные длины.
-
Выбрав единицу измерения , всегда можно измерить любой отрезок.
-
Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
-
Стандартной международной единицей измерения отрезков выбран метр.
2 вариант
-
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
-
Единицей измерения угла является миллиметр, сантиметр, дециметра.
-
Каждая сторона развернутого угла является продолжением другой стороны.
-
Градусная мера развернутого угла менее 1800.
-
Луч, исходящий из вершины угла и делящий его на две части, называется биссектрисой угла.
-
Угол называется прямым, если он равен 900.
-
Угол называется острым, если он больше 900.
-
Угол называется тупым, если он меньше 900.
-
Простейший прибор для измерения углов на местности является астролябия.
-
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются вертикальными.
-
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
-
Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
-
Равные отрезки имеют разные длины.
-
Выбрав единицу измерения , всегда можно измерить любой отрезок.
-
Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
-
Стандартной международной единицей измерения отрезков выбран метр.
-
Вертикальные углы равны.
-
Если угол острый, то смежный с ним угол также является острым.
-
Сумма смежных углов равна 180°.
-
Если угол равен 45°, то вертикальный с ним угол равен 45°.
-
Любые две прямые имеют ровно одну общую точку.
-
Через любую точку проходит более одной прямой.
-
Если угол равен 60°, то смежный с ним равен 120°.
-
Сумма вертикальных углов равна 180°
-
Через любые две точки можно провести прямую.
-
Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой.
-
Смежные углы равны.
-
Если угол равен 108°, то вертикальный с ним равен 72°.
-
Если угол равен 47°, то смежный с ним равен 143°.
-
Если две прямые перпендикулярны третьей прямой, то эти две прямые не пересекаются.
-
Через любую точку проходит ровно одна прямая.
-
Если угол равен 120°, то смежный с ним равен 120°
-
Всегда один из двух смежных углов острый, а другой тупой.
-
Через любые две точки можно провести прямую, и притом только одну.
Зачет № 2
ТРЕУГОЛЬНИКИ.
1 вариант
Установите верно или неверно высказывание
1. Все диаметры окружности равны между собой.
2. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
3. Каждая из биссектрис равнобедренного треугольника является его медианой.
4.В математике каждое утверждение, справедливость которого устанавливается путем рассуждения, называется теоремой, а само рассуждение называется доказательством теоремы.
5. Все хорды одной окружности равны между собой.
6. Любая высота равнобедренного треугольника является его биссектрисой.
7. Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
8. Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
9. Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.
10. Расстояние от точки, лежащей на окружности, до центра окружности равно диаметру.
11. Любая биссектриса равнобедренного треугольника является его медианой.
12. В любом треугольнике медианы пересекаются в одной точке.
13. Треугольник со сторонами 6 см, 8 см и 9 см является равнобедренным.
14. Предложение, в котором разъясняется смысл того или иного выражения или названия, называется определением.
Зачет № 2
ТРЕУГОЛЬНИКИ.
2 вариант
1. Сумма длин трех сторон треугольника называется его периметром.
2. Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
3. В математике каждое утверждение, справедливость которого устанавливается путем рассуждения, называется определение, а само рассуждение называется доказательством определения.
4. Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
5. Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
6. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
7. В любом треугольнике биссектрисы пересекаются в одной точке.
8. Треугольник со сторонами 6см, 8 см и 9 см не является равнобедренным.
9. В равнобедренном треугольнике углы при основании равны.
10. Предложение, в котором разъясняется смысл того или иного выражения или названия, называется теоремой.
11. Все хорды одной окружности равны между собой.
12. Самая большая хорда называется диаметром окружности.
13. Радиус окружности в два раза больше диаметра.
14. Часть плоскости, ограниченная окружностью, называется кругом.
Зачет №3. Параллельные прямые.
1 вариант.
Установите верно или неверно высказывание
1.Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
2. Две прямые на плоскости называются параллельными, если они пересекаются.
3. При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°.
4. Через любую точку проходит ровно одна прямая.
5. Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.
6. Если две прямые параллельны третьей прямой, то эти две прямые параллельны.
7. Если при пересечении двух прямых третьей прямой соответственные углы равны 37°, то эти две прямые параллельны.
8. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
9. Два отрезка называются параллельными, если они лежат на параллельных прямых.
10. Через любые две точки проходит прямая, и притом только одна.
11. Через точку, не лежащую на данной прямой , проходит только одна прямая , параллельная данной.
12. Если прямая пересекает одну из двух параллельных прямых, то она не пересекает другую.
13. Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.
14. Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 80° и 100°, то эти две прямые параллельны.
15. Если две параллельные прямые пересечены третьей прямой, то соответственные углы равны.
16. Если две параллельные прямые пересечены третьей прямой, то односторонние углы равны.
17. 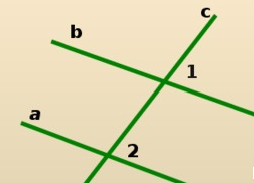 Углы 1и 2 на рисунке называются односторонние
Углы 1и 2 на рисунке называются односторонние
18. Углы 1и 2 на рисунке называются соответственные
19. Углы 1и 2 на рисунке называются накрест лежащие.
2 вариант.
Установите верно или неверно высказывание
1.Сумма внутренних накрест лежащих углов , образованных двумя параллельными прямыми и секущей, равна 1800.
2. Две прямые на плоскости называются параллельными, если они не пересекаются.
3. Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
4. Через любую точку проходит ровно одна прямая.
5. Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.
6. Если две прямые параллельны третьей прямой, то эти две прямые параллельны.
7. Если при пересечении двух прямых третьей прямой соответственные углы равны 54°, то эти две прямые параллельны.
8. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 180°, то эти две прямые параллельны.
9. Два отрезка называются параллельными, если они лежат на параллельных прямых.
10. Через любые две точки проходит прямая, и притом только одна.
11. Через точку, не лежащую на данной прямой , проходит только одна прямая , параллельная данной.
12. Если прямая пересекает одну из двух параллельных прямых, то она пересекает другую.
13. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
14. Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.
15. Если двух параллельные прямые пересечены третьей прямой, то соответственные углы равны.
16. Если две параллельные прямые пересечены третьей прямой, то сумма соответственных углов равна 1800
| 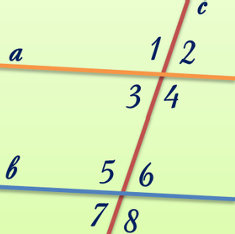
| 17.Углы 1и 5 на рисунке называются односторонние 18. Углы 6 и 2 на рисунке называются соответственные 19. Углы 4и 5 на рисунке называются накрест лежащие |
Зачет № 4. Соотношения между сторонами и углами треугольника.
1 вариант
Часть 1. Установите верно или неверно высказывание.
-
Сумма углов любого треугольника равна 360 градусам.
-
Треугольника со сторонами 1, 2, 4 не существует.
-
Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
-
Сумма углов любого треугольника равна 180° .
-
В треугольнике против большей стороны лежит больший угол.
-
Внешний угол треугольника равен сумме двух углов треугольника.
-
В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
-
В прямоугольном треугольнике гипотенуза меньше катета.
-
Если два угла треугольника равны, то треугольник равнобедренный.
-
Сумма двух острых углов прямоугольного треугольника равна 900.
-
Гипотенуза равна половине катета, лежащего против угла 300.
-
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
-
Все наклонные, проведенные из точки не лежащей на прямой, к этой прямой равны между собой.
-
Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой.
-
Сторона прямоугольного треугольника, лежащая против прямого угла, называется катетом.
-
Каждый угол равностороннего треугольника равен 60 градусов.
-
Треугольник АВС с углами 400 и 1000 является равнобедренным.
-
Углы при основании равнобедренного треугольника острые.
-
В треугольнике медиана меньше высоты, проведенной из той же вершины.
-
В равнобедренном треугольнике высоты, проведенные из вершин основания, равны.
Часть 2. Решите задачи.
-
Найдите угол А треугольника АВС, если угол В равен 78 градусам, а угол С на 23 градуса больше угла В.
-
Найдите угол при основании равнобедренного треугольника, если угол при вершине 84°.
-
В равнобедренном треугольнике СDЕ с основанием СЕ проведена высота СК. Найдите угол ЕСК, если угол D равен 54°.
-
Один из внешних углов равнобедренного треугольника равен 120°. Найдите углы треугольника.
Зачет № 4. Соотношения между сторонами и углами треугольника.
2 вариант
Часть 1. Установите верно или неверно высказывание.
-
Сумма углов любого треугольника равна 180 градусам.
-
Треугольника со сторонами 1, 2, 5 не существует.
-
Длина гипотенузы прямоугольного треугольника больше суммы длин его катетов.
-
Сумма углов любого треугольника равна 360°
-
В треугольнике против меньшей стороны лежит меньший угол.
-
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
-
В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
-
В прямоугольном треугольнике гипотенуза меньше катета.
-
Если два угла треугольника равны, то треугольник равносторонний.
-
Сумма двух острых углов прямоугольного треугольника равна 900.
-
Катет, лежащий против угла 600, равен половине гипотенузы.
-
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
-
Все наклонные, проведенные из точки, не лежащей на прямой, к этой прямой равны между собой.
-
Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой.
-
Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой.
-
Каждый угол равностороннего треугольника равен 50 градусов.
-
Треугольник АВС с углами 500 и 800 является равнобедренным.
-
Углы при основании равнобедренного треугольника острые.
-
Острый угол равнобедренного прямоугольного треугольника равен 45 градусов.
-
Перпендикуляр, проведенный из точки к прямой, больше любой наклонной, проведенной из той же точки к этой прямой.
Часть 2. Решите задачи.
-
В треугольнике угол С = 90°, угол А = 30°. Найти угол В.
-
Найдите угол при основании равнобедренного треугольника, если угол при вершине 70 градусов.
-
Найдите угол А треугольника АВС, если угол В равен 78 градусам, а угол С в 2 раза меньше угла В.
-
В равнобедренном треугольнике АВС c основанием АС проведена биссектриса АD.Найдите угол ADC, если угол С = 60°.







 Углы 1и 2 на рисунке называются односторонние
Углы 1и 2 на рисунке называются односторонние



















