Просмотр содержимого документа
«Зачеты для 9 класса подготовка к ОГЭ»
Вариант
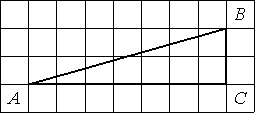
1. Найдите тангенс угла В треугольника АВС, изображённого на рисунке.
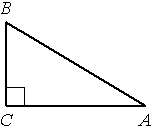
2. В треугольнике ABC угол C прямой, ВС = 6, sinA = 0,6.
Найдите AB.
3. В треугольнике АВС углы А и С равны 20º и 60º соответственно. Найдите угол между высотой ВН и биссектрисой BD.

4. Два острых угла прямоугольного треугольника относятся как 2:3. Найдите больший острый угол. Ответ дайте в градусах.
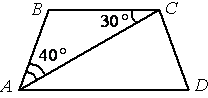
5. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
6. Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.
Вариант
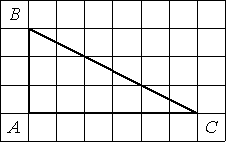
1. Найдите тангенс угла В треугольника АВС, изображённого на рисунке.
2. В треугольнике ABC угол C прямой, АС = 8, cosA = 0,8.
Найдите AB.

3. В треугольнике АВС углы А и С равны 20º и 50º соответственно. Найдите угол между высотой ВН и биссектрисой BD.

4. Два острых угла прямоугольного треугольника относятся как 1:29. Найдите больший острый угол. Ответ дайте в градусах.
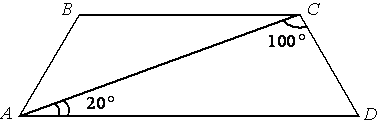
5. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
6. Разность углов, прилежащих к одной стороне параллелограмма, равна  . Найдите меньший угол параллелограмма. Ответ дайте в градусах.
. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
7. Углы выпуклого четырехугольника относятся как 8:9:11:17. Найдите меньший угол. Ответ дайте в градусах.
8. В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25º. Найдите величину угла ОСД
9. Точка О – центр окружности,
Найдите величину угла ACB

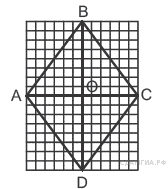
10. На рисунке изображен параллелограмм  . Используя рисунок, найдите
. Используя рисунок, найдите 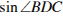 .
.
7. Углы выпуклого четырехугольника относятся как 2:9:10:19. Найдите меньший угол. Ответ дайте в градусах.
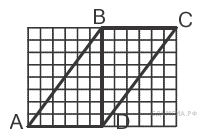
8. В окружности с центром в точке О проведены диаметры AD и BC, угол АВО равен 55º. Найдите величину угла ОDС.
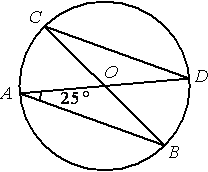
9. Точка О – центр окружности,
Найдите величину угла AOB.

10. На рисунке изображен ромб  . Используя рисунок, найдите
. Используя рисунок, найдите  .
.
 Решение.
Решение.
Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему. Треугольник 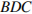 — прямоугольный, поэтому
— прямоугольный, поэтому 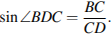
Вычислим по теореме Пифагора длину гипотенузы 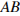 :
:
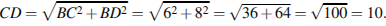
Тогда
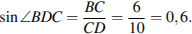
Ответ: 0,6.
Ответ: 0,6
Решение.
Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему. Треугольник 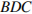 — прямоугольный, поэтому
— прямоугольный, поэтому 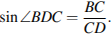
Вычислим по теореме Пифагора длину гипотенузы 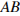 :
:
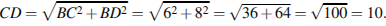
Тогда
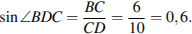
Ответ: 0,6.
Ответ: 0,6
















 Решение.
Решение. 









