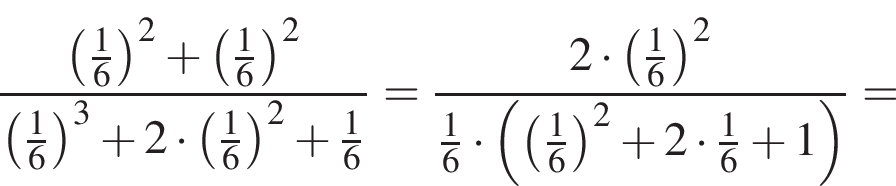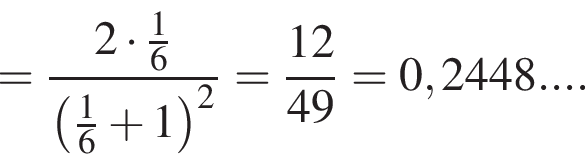Задачи ЕГЭ по математике, решаемые с помощью графов

Задачи ЕГЭ по математике, решаемые с помощью графа – дерева.

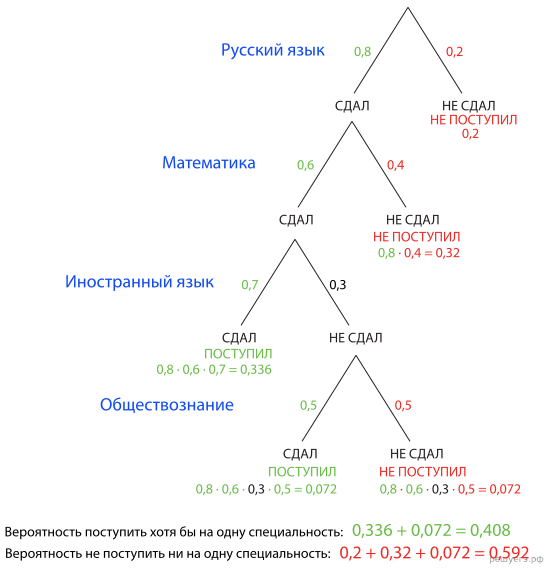
1. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов  — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов  — математика, русский язык и обществознание.

Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку  — 0,8, по иностранному языку  — 0,7 и по обществознанию  — 0,5.

Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.

Решение с помощью двоичного дерева.

1. Правильный игральный кубик бросали до тех пор, пока сумма выпавших при всех бросках очков не стала больше чем 3. Известно, что общая сумма очков оказалась равна 4. Какова вероятность того, что был сделан ровно один бросок? Ответ округлите до сотых.

Решение. Пусть событие A состоит в том, сумма всех выпавших в результате одного или нескольких бросаний очков равна 4. Построим дерево вариантов, приводящих к этому событию. Исходы приводящие к этому событию отмечены оранжевым цветом.

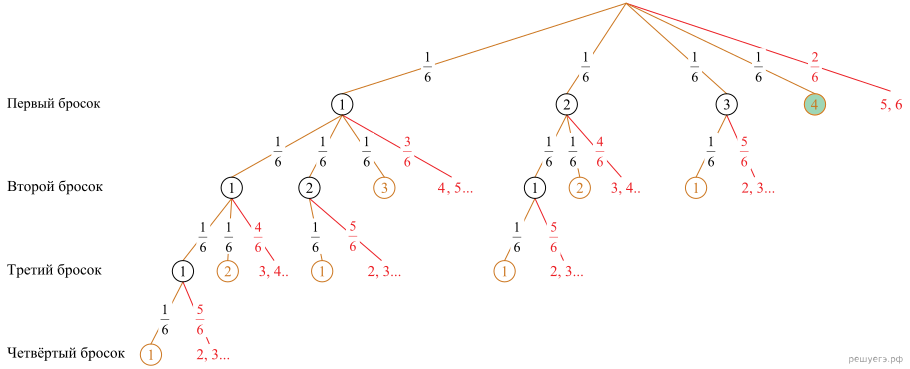
Найдем вероятность P(A):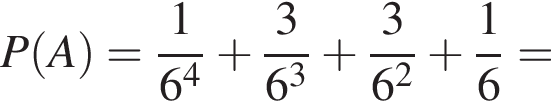

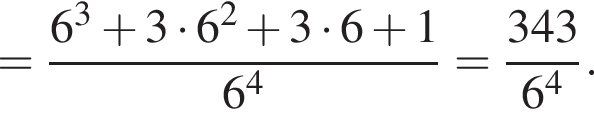
Пусть событие B состоит в том, что был сделан один бросок. Тогда искомая вероятность P(B|A) события В при условии, что событие А наступило (вероятность того, что был сделан один бросок, при условии что выпало 4 очка) определяется по формуле условной вероятности 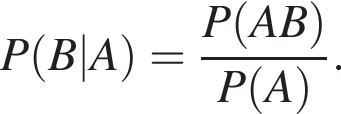Вероятность произведения событий B и A, то есть события, в котором при первом бросании кости выпало 4 очка (выделено салатовым цветом), равна 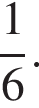Тогда для искомой вероятности получаем:

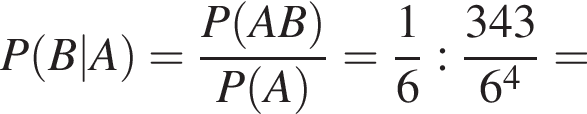
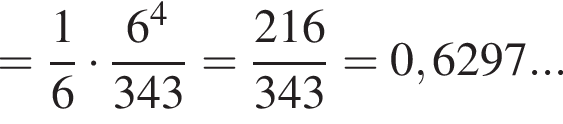
Округляя до сотых, получаем 0,63. Ответ: 0,63.

1. Правильный игральный кубик бросали до тех пор, пока сумма выпавших при всех бросках очков не стала больше чем 2. Известно, что общая сумма очков оказалась равна 3. Какова вероятность того, что было сделано ровно два броска? Ответ округлите до сотых.

Решение. Изобразим с помощью дерева возможные исходы. Зелёным цветом отмечены исходы, удовлетворяющие условию «сумма выпавших очков равна 3». Оранжевым цветом отмечены исходы, удовлетворяющие условию «сумма очков, выпавших ровно за два броска равна 3».

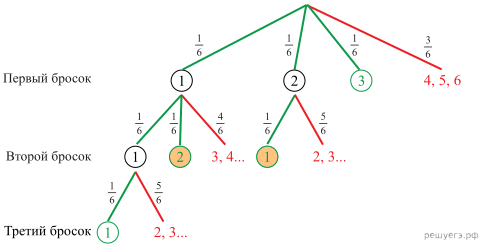
Вероятность события «сделано два броска» при условии «в сумме выпало 3 очка» равна:

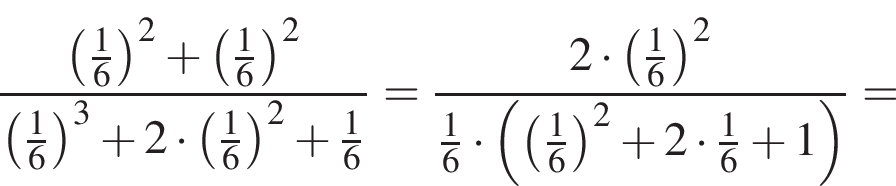
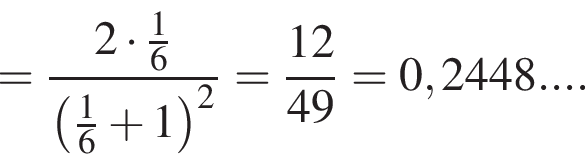
Округляя до сотых, получаем 0,24. Ответ: 0,24.

1. В городе 48 % взрослого населения  — мужчины. Пенсионеры составляют 12,6 % взрослого населения, причём доля пенсионеров среди женщин равна 15 %. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».

Решение. Пусть х  — доля мужчин-пенсионеров среди всех мужчин. Построим дерево вероятностей

Пенсионеры составляют 0,126 взрослого населения города, откуда получаем:

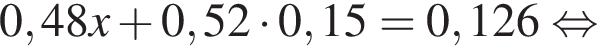
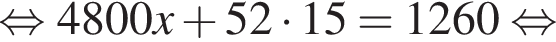
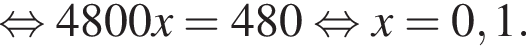
Т.о., вероятность того, что случайно выбранный мужчина окажется пенсионером, равна 0,1.

1. Артём гуляет по парку. Он выходит из точки S и, дойдя до очередной развилки, с равными шансами выбирает следующую дорожку, но не возвращается обратно. Найдите вероятность того, что таким образом он выйдет к пруду или фонтану.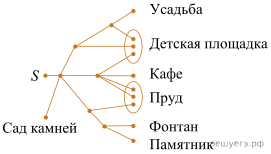

Решение. Чтобы выйти к фонтану Артёму нужно пройти три развилки. На первой развилке нужно выбрать одну из четырёх дорожек, на второй  — одну из двух, на третьей  — одну из двух. Значит, вероятность выйти к фонтану равна 0,25·0,5·0,5=0,0625.

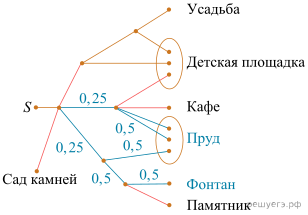
Выйти к пруду Артём может двумя разными способами. Первый способ: на первой развилке нужно выбрать одну из четырёх дорожек, на второй  — одну из двух. Вероятность этого способа равна 0,25·0,5=0, 125. Второй способ: на первой развилке нужно выбрать одну из четырёх дорожек, на второй  — две из четырёх. Вероятность этого способа тоже равна 0,25·0,5 = 0,125.

Значит, вероятность того, что Артём выйдет к пруду или фонтану, равна 0,0625+0,125+0,125=0,3125. Ответ: 0,3125.