Задачи гидростатика

ГИДРО- и АЭРОСТАТИКА

0а)_Каково давление воды на дно в точках А, В, С (рис.4)? Атм давление не учитыв.

0б) В сосуд, имеющий форму куба с ребром а, налита доверху жидкость плотн ρ. Опр силы давл жидк на дно и на стенки сосудов. Ат давление не учитывайте.

А). Когда жидк покоится, давл во всех т, леж на 1 урне, одинак: разн давл вызв бы перетек жидк. След, p_A=p_B=p_C. В т же С p_C=ρgh, где ρ – плотн воды. При выч давл жидк глубину след отсч от своб поверхн этой жидкости. Иначе аквалангист, заплыв на 100м глубине в низкую подв пещеру, м бы «спрятаться» от давл воды.

Б) Давл жидкости на дно сосуда = весу столба жидкости выс а с пл осн=1: p₁=ρgа.

Сила давл на дно сосуда:F₁=p₁S=ρga³. Давл на бок грань куба б завис от расст до поверхн жидк. На глуб h давлp=ρgh. Тк давл изм с глуб по лин закону, то для опр силы давл н ср давл p_ср= ρgh+0/2= ρgh/2.

умн на площадь боковой грань: F₂= ρga³/2.

В) На гориз листе резины лежит переверн кастрюля ра R=10 см и выс H=15 см. В дне кастр просв круглое отв  r=1 см, в кот плотно вставл легкая вертик трубка В кастр через трубку налив воду. Когда вода заполн всю каст и подним по трубке на h=4 см, она нач вытекать из-под краев кастрюли. Какова масса m кастр?

Вода нач вытекать, когда кастр чуть приподн напр вверх сила давл воды на дно. Эта сила F=pS д уравновесить дейст на кастр силу тяжести mg. p=ρgh  ,

pS=mg откуда

г) Оцените массу атм Земли (радЗемли R = 6400 км).

Вес атм = силе давл воздуха на всю поверхн Земли, пл кот где p_а = 50 Па

Такая п оценка массы атм воз потому, что осн часть атм сосред на высотах, малых по ср с рад Земли. Поэтому м счит, что вес атм = mg,

1. В цилиндрич сосуд радиуса R наливают жидкость.

А)До какой высоты h н налить жидк, чтобы сила, с кот жид­кость давит на бок поверхн сосуда, была = силе давл на дно? Б)Б ли завис сила давл на дно от формы сосуда при одном и том же ур-не жидк? Отв: h = R.

2. В цилиндр сосуд налиты равные массы воды и ртути. Плот­н ртути 13600 кг/м3, воды 103 кг/м3. Общая высота столба жидк-тей 143 см.а)Найти давл на дно сосуда. Отв: 26.1 кПа.

Б)Нарис график зти гидростатич давления от глубины.

2) Сосуд неизв объёма доверху наполн неизв жидк. Как найти плотн жидк, если в вашем распор имеется медная деталь неправ формы и весы? Опиш посл-ть ваших действий.

3. Для откач воды из подвала исп насос мощн 300Вт. Ширина подвала 6м, длина 24 м, высота 4м.Перед нач откач уровень воды в подвале нах на уровне земли. Ск врем займёт откачив? в проц откачив мощн насоса ост неизм. Отв 47 часов.

З 1.23 (Сосуд) На шерохов поверх стола стоит шир сосуд масс m. Пл дна сосуда S. В бок стене у самого дна имеется закрытое пробкой отв сеч σ. В сосуд налив воду. Когда высота воды в сосуде достиг вел h, пробка выскальз из отв, и сосуд прих в движ с ускор a. Найти коэф тр между дном и поверхн стола. Каков д б коэф тр, чтобы сосуд остался на месте после выскальз пробки

1)Льдина пл попер сеч S = 1 м2 и толщ Н = 0,4 м плавает в озере. Какую работу н соверш, чтобы полн погрузить льдину в воду? Плотн льда

2) Тонкая палоч (рис.) длин l=40см, сдел из материала плотн ρ = 0,22 г/см3, шарн подвеш к потолку на высоте h так,что нижн ее конец погружен в жидк, С Плотн ρ0=0,8г/см3 Опр длину погруж части палочки l0.

3) В сосуд, напол заполн жидк плотн ρ, опускают удерж в верт полож цилиндр, по высоте = высоте сосуда (рис). Цилиндр оказ в равнов, когда от его нижн края до дна ост 1/4 высоты сосуда. Чему= плотн м-ла цилиндра, если его сеч S , а сеч сосуда S0 Трения нет.

4) Цилиндр пробирка с дробью внутри, имеющ пл попер сеч S =l см2 плавает в воде вертик, причем из воды высов часть пробирки выс h =5см . Какова мин плотн жидк, в кот пробирка с груз не утонет, если сумм масса пробирки и грузика М =20 г? Плотн воды

Сообщающиеся сосуды

1) В U-обр трубке нах ртуть, вода и керосин . Найдите высоту столбов воды и керос, если в правом колене трубки ур-нь ртути на h = 1 см выше, чем в левом.

2) При равнов поршень в 1 из сообщ сосудов (рис) устан на h₁ = 20 см выше, чем во 2м. Массы поршн m₁ = 2 кг и m₂ = 4 кг. Если на 1 поршень пост гирю  m₃ = 3 кг, то поршни устан на одинак высоте. Как распол поршни, если гирю переставить на 2 поршень?

Реш1) Пусть высота столба керосина (рис.9) h_к, тогда высота столба воды h_в = h_к + h. Давление в т А и В д б одинак: h_к = h(ρ_рт-ρ_в)/(ρ_в-ρ_к) = 63 см. Отсюда h = 64 см.

Реш2)  когда поршни устана на разных урнях, следует учит и давл столба жидк. Если перест гирю на 2 поршень, он окаж ниже 1го. Обоз разность высот порш в этом сл h, плотн жидк ρ, а пл поршн S₁ и S₂ и учит, что сила давл жидк на поршень при равнов = по мод весу этого поршня с грузом, получ систему

m₃ = ρh₁S₁ и m₃ = ρS₂(h – h₁), откуда h = h₁(1 + S₁/S₂). Поск из 2 ур следует, что S₁/S₂ = (m₁ – m₃)m₂, находим: 1й поршень б распол выше 2го на h = h₁(m₁ + m₂ + m₃)/ m₂.

Гидравл машины

1). Какую силу F н приложить к малому поршню гидр машины, чтобы большой поршень м поднять груз  m = 600 кг? Пл поршней S₁ = 0,5 см² и S₂ = 30 см².

Реш. Отн сил, дейст на поршни = отн пл этих поршн:F₁/F₂ =S₁/S₂или F/S₁=mg/S₂. Отсюда F =mgS₁/S₂ =100Н.

2). Действие гидравл машины осн на зне Паскаля, кот вып для жидк и газов. М ли в гидравл машине заменить жидкость газом?

Реш. Из-за сжимаем газа в нем трудно создать большое давл, поэтому такая машина не б созд большой силы.

1)Первонач в сооб сосудах нах ртуть ( рис). После того как в узкий сосуд налив столб воды высотой 68 см ртуть подним в шир сосуде на … мм? Плотн ртути 13,6×10³ кг/м³, плотн воды 1,0 × 10³ кг/м³. 1) 1; 2) 10; 3) 100; 4) 25; 5) 5.

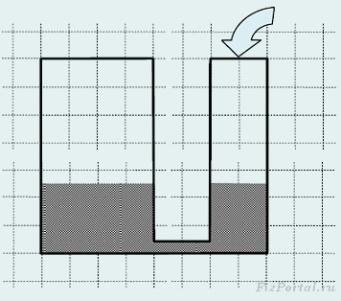
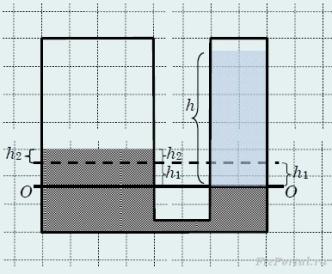
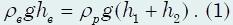
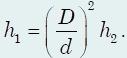
2) В сообщ сосудах нах ртуть. Пл сеч 1 сосуда в 2 р пл др. Шир сосуд долив водой до края. На ск см подниме урнь ртути в др сосуде? Первонач уровень ртути б распол на h=36,8 см ниже верхн края сосуда. Плотн ртути в 13,6 раз плот воды.

 Реш  В шир сосуд придется долить воды высо h + h₁,где h₁ –это выс опусr ртути в шир сосуде. При этом ртуть, по отy к св первонач полож, подним на высоту h₂.  Высоты h₁ и h₂ свяжем, вос рав объемов ртути, в силу ее не сжим h₁S₁ = h₂S₂,т к, по усл задачи S₁/S₂ = 2, то h₂ = 2h₁.
Давл, созд водой в шир сосуде б= давл ртути в узком сосуде ρ_вg(h + 2h₂) = ρ_pg(h₂/2 + h₂).
Отсчет высоты вед от нижн урня ртути в шир сосуде. Решим посk ур отн высоты.

ρ_вh + 2ρ_вh₂ = (3/2)ρ_ph₂. Откуда h₂ = ρ_вh/((3/2)ρ_p − 2ρ_в). После вычисления h₂ = 2 см.

3)В сообщ цилиндр сосудах диам кот отлич в 2 р нах ртуть. В узкий сосуд наливают столб воды высотой . На ск изм уровни ртути в сосудах отн первонача? Плотности воды и ртути

4а)Ведро изг в виде усечен конуса с дном рад R и рад верхней части 2R напол доверху жидк массы m Опр давл и силу давления на дно и стенки. Атм давл пренебречь

б)решить з-чу если ведро имеет форму переверн усеч конуса с дном рад 2R

5)при подъеме груза массой M с пом гидравл пресса была соверш работа А. При этом малый поршень сделал n ходов перемещ за 1 ход на h. Во ск раз отлич площади поршней?

6) Тонкосте стакан массы m, распол верт вниз дном, плавает на гр-це раздела 2 жидк с пл-тями ρ1 и ρ2. Найти глубину погруж стакана в нижн жидкость, если дно стакана имеет толщ h и пл S . Массой стенок стакана пренебр.

усл равнов Из з-на Паскаля

УСЛОВИЕ ПЛАВАНИЯ ТЕЛ»

Пр льдинка плавает на грце между водой и керосином. Какая часть ее объема нах ниже границы раздела жидкостей, если керосин покрывает льдинку полностью?

Реш. Усл плавания F_A = mg,где m = ρ_ЛV – масса льдинки, V – ее объем.

Арх сила F_A = ρ_ВgV + ρ_Kg(V- V_B),где V_B – объем вытес воды. Отсюда V_B/V = (ρ_Л - ρ_K)/(ρ_{В -} ρ_K)=0,5.

Пр2 Легкий спл конус погруж в воду один раз верш вверх, а др раз – верш вниз В каком сл н совершить большую работу для полного погруж конуса? Одинак ли по модуля силы Арх действ на полн погруж в воду конус в 1 и 2 сл?

Реш больший объем воды вытесн конус, распол верш вверх. След, в этом сл на конус б действ большая сила Архимеда, и поэтому в процессе погруж придется прилаг большую силу. Когда конус погруж полн, объем вытесн им воды в любом сл = объему конуса нез от его располож.

0.Лодка плавает в мален бассейне. Как изм ур-нь воды в бассейне, если выброс из лодки в бассейн камень?Отв.уменьш, и уровень воды в бассейне пониж

4. Полый шар изг из материала с плотн 3 г/см3. Рад шара 20 см. а)Каков д б мах рад полости, чтобы шар утонул в воде, плотн кот 1 г/см3? Отв: 17.4 см. б)Как изм рез-т п.1), если воду замен жидкостью с плотн в 1,5 раза большей, чем у воды?

Закон архимеда

Пр1  Кусок железа в воде весит 1,67 Н. Найти его объём. Плотность железа 7,8г/ см³.

Реш. Вес в воде уменьш за счёт силы Архимеда:где- вес железа в воздухе.Тогда:,отсюда.

Пр2) Какое наим число брёвен длиной 10м и пл сеч 300см² н взять для плота, чтобы перепра на нём через реку автома массой 1000кг. Счит плотность дерева 800кг/м³.

Реш. Чтобы перепр машину на плоту, н вып усл плавания:. где m₁-масса n-числа брёвен плота, а m₂-масса автом., аТогда. Отсюда . .

N== N=

1) Опр подъемную силу аэростата вмещающего 5000 м³ водорода, если масса оболочки гондолы со всем оборуд =1000 кг.

3. Медный шар с внутр полостью весит 2.59 Н в возд и 2.17 Н в воде. Плотн воды и меди 1 и 8.9 г/см3 соотв. А)Опр объём внутр полости. Отв: 13 см3.

Б)Как по характ погруж шара в воде м опр полож полости, если она несимм отн ц шара?

5. Кусок металла, сплав меди и серебра, в воздухе имеет вес Р1=2.5 Н, а в воде Р2=2.25 Н. Плотн серебра ρс=10.5 г/см3,меди - ρм=8.9 г/см3, воды - ρв= 1 г/см3. А)Опр массу серебра и меди в этом куске сплава. Отв: 184 г ,71 г.

Б)Изм ли вес металла в воде, если внутри куска окаж маленькая замкн полость? Отв поясн.

6. Кусок пробки массой 1.2 г привязан к куску железа массой 11.7 г. При погруж этих связ тел в воду их вес сост 64 мН. А)) Опр плотность пробки. Плотн железа 7.8 г/см3. Отв: 0.246 г/см3.б)) Какая часть объема пробки окаж погруж в воду, если ее отвяз от куска железа?

7. Для опр плотн неизв жидко однор тело подвес на пружин весах в этой жидкости, а затем - в вакууме и в во­де. Оказ, что тело весит 1.66 Н в жидкости, 1.8 Н в вакууме и 1.6 Н в воде.

А)Найти плотн жидк и тела. Отв700 кг/м; 9000 кг/мЗ. Б)Как повлияет изм атм давл на рез измер?

8. Льдина равном толщ плавает, выст над ур-нем воды на 2 см. Пл основ льдины 200 см2, плотн льда и воды 0.9 и 1 г/смЗ. А)Найти массу льдины. Б)Какой мин груз н полож на льдину, чтобы её утопить? Ответ: 3.6 кг.

9. В стак с водой плавает в верт полож брусок в форме прямоуг параллелепип. Брусок длиной 3 см имеет кв сеч со стор 1 см. а)Как из расст от поверхн воды до ниж грани бруска, если брусок перев в гориз полож? Б)Как при этом изм урнь воды в стакане? Отв: уменьш в 3 раза.

10. В сосуде с ртутью плавает шарик масс 100 г, напол погру­ж в ртуть. В сосуд долив воду так, что она полн покрывает плав шарик. Плотн ртути 13.6 г/см3, воды 1 г/см3.

А)Какая часть объема шарика окаж при этом погр в ртуть? Отв: 0.46

Б)Чему = сила Архимеда, действ на этот шарик, если его опустить в большой сосуд с водой?.

11Груз, прикрепл к 3 одинак воздуш шарам, под­ним с пост скор. Массы оболоч шаров и сопрот воздуха пренебр малы. А)С каким ускор б двиг сма, если один из шаров лопнет? Б)Как изм это ускор, если газ в шарах нагреть? Шары герметич­ и сдел из тонк эластич м-ла.Отв: g/3.

12. Для подъем со дна водоема груза объем 0.1 м3 и плотн 2700 кг/м3 к нему привяз полый шар

массой 2 кг.1) Какой объем д иметь полость шара, чтобы груз равном подни­м к поверхн? Сопр

воды пренебр.2) Как соотн силы Архимеда, действ на каждое из тел?Ответ: 0.172 м3.

13. Плоская шайба высотой Н из м-ла плотн р плавает на гр-це разд 2 жидк. Плотн верхней жидк ρ1, нижней ρ2 (ρ2 ρ ρ1). Верхняя жидк полн покрыв шайбу. А)На какую глуб погруж шайба в нижнюю жидк? Огв: h = H(ρ – ρ1)/(ρ2 – ρ1). Б)Нарис з-ть гидростатич давл от глуб, если толщ кажд из слоев жидкости= толщ шайбы.

14. В сосуде 2 несмешив жидкости с плотн 1 г/см3 и 2 г/см3, толщины этих жидк 10 см и 15 см соотв. С поверх верхней жидк в сосуд опуск без нач скор маленьк обтекаем тело, кот достиг дна в тот момент, когда его скорость стан =0.

А)Какова плотн тела? Трение не учит. Отв: 1.6 г/см3. Б)Нарис график з-ти гидрост давл от расст до поверхн верхней жидкости.

15. Полый стальн куб со стороной 1 м, заполн наполов во­дой, плавает в воде так, что его нижняя грань распол гориз. Толщ стенок куба 4 мм. Плотность стали 7.8 г/см3.

А)Опр глубину погруж нижней грани куба. Ответ: 67.6 см. б)Какая часть объема тела окаж погруж в жидк, если плот­н тела в n раз меньше плотн жидк?

16. Полый алюм кубик плавает в воде, погрузивш в неё на 60% св объёма. Полость напол заполн жидк. В рез=те над поверхн воды стало выступ 5% объема кубика. Плотн алюм 2700 кг/м3, воды - 1000 кг/м3.А)Найти плотн жидк, залитой в полость. Отв: 900 кг/м3. Б)Какую часть объёма кубика занимает полость?

17. Тонкая однор палочка шарн закрепл за верхн конец. Нижн конец палочки погр в воду. При равнов под водой нах 0.2 длины палочки.А)Найти плотн м-ла палочки. Отв: 360 кг/м3. Б)Как изм глубина погруж палочки, если темпер жидкости возрастёт?

18. Тонкий стерж массой 1 кг шарн закрепл одним концом, опущен в воду так, что др его конец упирает в дно, а поло его длины оказ под водой. Плотн м-ла стержня в 2 р плотн воды.а)Опр силу давл стержня на дно.Отв: 3.06 Н. б)Как изм эта сила, если стержень окаж под водой полн?

19. Тонкий длинн цилиндр поплавок массой 2 г с привяз к одному из его концов грузиком плавает в воде, погрузивш в неё на 2/3 своей длины. Ось поплав образ с поверхн воды нек угол.

А)Найти натяжение нити, связыв поплавок с грузиком.

Б)От чего зависит сила Архимеда, дейст на поплавок?Ответ: 9.8 мН.

20. К концу тонк прямого металл стержня длины 1 м прикрепл шарик рад 10 см и массой 10 г так, что его ц т ле­жит на продолж стержня. Стерж с шариком опуст в водоём, глуб кот меньше 1 м. В рез шарик оказ погруж в воду напол, а стержень одним концом упир в дно водоёма.

а)Считая объём стержня пренебр малым, найти силу, с кот он действует на дно водоёма.

Б)Какую силу н приложить к шарику, чтобы полностью погрузить его в воду?Отв: 24.5 Н.

21. К концу однор палочки длиной 20 см и массой 4 г подвеш на тонкой нити алюм шарик рад 5 мм. Палочку кладут на край сосуда с водой, добив равнов при погруж в воду полов ша­рика.  Плотн алюм 2700 кг/м3, воды - 1000 кг/м3. А)Опр, на каком расст от края сосуда подвеш шарик. Отв: 7.76 см. б)Как изм резт п.1), если воду замен маслом с плотн, меньшей плотн воды?

22. Два шарика объемом 10 см3 каждый разной массы, связа невес нерастяж нитью, погружены в воду. Сила натяж нити 12 мН. А)Найти отн масс шарик, если легкий шарик окаж погруж в воду напол Отв: 2.95..б)Нарис график з-ти силы Архим от объема погруж в воду части шарика.

23. Тело объемом 1 м3 и массой 2400 кг удержив в водоеме на глу­бине 20м.

А)Какую работу н соверш, чтобы за 20 с поднять тело к по­верхн? Силой сопр воды пренебр.

Б)Нарис зть гидростатич давл и силы Архимеда от глубины. Ответ: 285 кДж.

24. Однор кубик плотн 0.7 г/см3 со стор 0.5 м плавает в воде. А)Опр мин раб, необх для того, чтобы погру­з его в воду полн. Б)Нарис график зти силы Арх от полож ц м куб отн поверх воды.

1)Маленький деревянный шарик погрузили в воду на глубину H и отпустили. На какую высоту над поверхностью воды поднимется шарик

Реш. Выберем 0-отсч потенц эн на уровне воды. Тогда на глубине h

В наивысшей т подъема x механич эн откуда

2)В сосуде с накл дном наполн жидк с плотн на дне стоит кубик Найти силу давл кубика на дно. Расст от верхнего ребра кубика до поверхн воды h, угол наклона дна к гориз α. Между

дном и нижней гранью кубика вода не проникает. Ребро кубика l. Отв

1 слаг составл силы тяжести, действ на кубик, 2е — сила давл столба воды над кубиком; эта сила давл напр по нормали к грани.

3) Отверстие в гориз дне сосуда закрыто лёгким полусферич колпачком рад R. Сосуд наполнен жидкостью плотн ρ. Дно нах на глубине H. Найдите силу, с кот колпачок давит на дно сосуда. Ускор св падения g. Объём шара

реш Т к колпачок лёгкий, то иск сила = весу жидк, нах непо-сре над ним. Пусть V — объём этой жидкости тогда

3)На поверхн воды плавает деревян брусок кв сечения, имеющ плотн

Какое из 2 полож равновесия, показ на рис, б устойчивым и почему?

Потенц эн бруска в обоих сл одинак, а потен эн воды—нет. Как несл убедиться, равнов в промеж полож меж указ положен нет. Поэтому равнов бруска устой в том сл когда ц т вытеснен воды распол выше: если сторону квадр в сеч бруска принять за 1, то

где h — расст по верт от ц т вытесн воды до ц т бруска. Зн, полож2 устойч. К такому же рез прив анализ устойчи, провед исх из сравн вращ моментов сил при небольшом откл бруска от положения равновесия

4) Цилиндрич ведро, напол заполн водой, жёстко закрепл на краю лопасти ветр мельницы ( рис). При какой угл скор ω вращ лопастей вода не б вылив из ведра? Длина лопасти L мн больше высоты ведра h и диам его дна d. Ускор своб падения g.

Опр полож поверхн воды в ведре в мом, когда лопасть сост нек угол α с вертик. Ур движ эл жидк, нах вблизи её поверхн где -архим сила, дейст на данный эл

в равнов напр архим силы перпенд к своб поверхн жидкости; с др стор, из-за малости разм ведра перех процессы быстротеч, и воду в каждый мом врем м считать нах в равнов. Из ур получ, что поверхн воды в ведре перпенд вектору пусть угол откл

вект Вода не б выливаться из ведра, заполн наполовину, если откуда

5 Переверн вверх дном стакан погруж в водоем. На какой глубине стакан нач тонуть?:

Плотн воды ρ = 10³ кг/м³.Атм давл 10⁵ Па. Объем стакана V=200 мл = 200∙10^–3 л = 2∙10^–4 м³.Масса стакана m=50 г = 5∙10^–2 кг

Реш Уменьш объема вытесн жидк м происх за счет сжатия воздуха в стак, кот, в св оч м идти за счет увел давл. Изм темпер, по мере погруж стакана, м не учит, Связь давления газа и его объема при пос температуре выр з Бойля–Мариотта.Давл жидк действ увел с глуб и перед во все стороны, в ч и вверх, одинаково.Гидростатич давл прямо пропорц плотн жидк и ее высоте (глуб погруж).

(+)

5)На квадр деревянн плоту разм 2 × 2 × 0,3 м, сде из дерева плотн 800 кг/м³, стоит физик массой  80 кг. На какое расст от центра плота он должен отойти, чтобы край плота окунулся в воду?

6)Сферу радиусом R, составл из двух одинак плотно пригнанн тонкостен полусфер массой m каждая, наполт жидкостью плотн ρ. 1) Какую вертик силу н приложить к нижней полусфере, чтобы жидкость не вылив, если вер сфера закреплена? 2) С какой силой надо сжимать левую и правую полусферы, чтобы жидкость не выливалась?

Олимпиада мфти 8 кл

2.Сосуд неизв объёма доверху наполн неизв жидк. Как найти плотность жидкости, если в вашем распор имеется медная деталь непр формы и весы? Опишите посл-ть ваших действий.