Задачи на движение по воде

Задачи на дви­же­ние по воде

1. Из пунк­та А в пункт В, рас­по­ло­жен­ный ниже по те­че­нию реки, от­пра­вил­ся плот. Од­но­вре­мен­но нав­стре­чу ему из пунк­та В вышел катер. Встре­тив плот, катер сразу по­вер­нул и по­плыл назад. Какую часть пути от А до В прой­дет плот к мо­мен­ту воз­вра­ще­ния ка­те­ра в пункт В, если ско­рость ка­те­ра в сто­я­чей воде вчет­ве­ро боль­ше ско­ро­сти те­че­ния реки?

Ре­ше­ние.

Пусть ско­рость те­че­ния реки (и плота)   км/ч. Тогда ско­рость ка­те­ра про­тив те­че­ния равна   км/ч, а по те­че­нию   км/ч. Сле­до­ва­тель­но, ско­рость ка­те­ра про­тив те­че­ния в 3 раза боль­ше ско­ро­сти плота, а по те­че­нию — в 5 раз боль­ше ско­ро­сти плота. Если плот до встре­чи про­плыл   км, то катер — в 3 раза боль­ше, т. е.   км. После встре­чи катер прой­дет   км, а плот — в 5 раз мень­ше, т. е.   км. Всего плот прой­дет

.

От­но­ше­ние прой­ден­но­го пло­том пути ко всему пути равно  .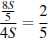

Ответ: плот прой­дет    всего пути.

2. Рас­сто­я­ние между при­ста­ня­ми А и В равно 80 км. Из А в В по те­че­нию реки от­пра­вил­ся плот, а через 2 часа вслед за ним от­пра­ви­лась яхта, ко­то­рая, при­быв в пункт В, тот­час по­вер­ну­ла об­рат­но и воз­вра­ти­лась в А. К этому вре­ме­ни плот про­шел 22 км. Най­ди­те ско­рость яхты в не­по­движ­ной воде, если ско­рость те­че­ния реки равна 2 км/ч. Ответ дайте в км/ч.

Ре­ше­ние.

Обо­зна­чим ис­ко­мую ско­рость (в км/ч) за   . Плот прошёл 22 км, зна­чит, он плыл 11 часов, а яхта 9 часов. Таким об­ра­зом, имеем:

, 
от­ку­да на­хо­дим   .

Ответ: 18 км/ч.

3. Мо­тор­ная лодка про­шла 36 км по те­че­нию реки и вер­ну­лась об­рат­но, по­тра­тив на весь путь 5 часов. Ско­рость те­че­ния реки равна 3 км/ч. Най­ди­те ско­рость лодки в не­по­движ­ной воде.

Ре­ше­ние. Обо­зна­чим   км/ч ис­ко­мую ско­рость. По те­че­нию реки лодка дви­га­лась  ч. 
Про­тив те­че­ния лодка шла   ч. По­лу­ча­ем урав­не­ние

. 

Решим его:

Корни квад­рат­но­го урав­не­ния: 15 и −0,6. Сле­до­ва­тель­но, ско­рость лодки равна 15 км/ч.
Ответ: 15 км/ч.

4. Ры­бо­лов в 5 часов утра на мо­тор­ной лодке от­пра­вил­ся от при­ста­ни про­тив те­че­ния реки, через не­ко­то­рое время бро­сил якорь, 2 часа ловил рыбу и вер­нул­ся об­рат­но в 10 часов утра того же дня. На какое рас­сто­я­ние от при­ста­ни он от­да­лил­ся, если ско­рость реки равна 2 км/ч, а соб­ствен­ная ско­рость лодки 6 км/ч?

Ре­ше­ние.

Пусть ис­ко­мое рас­сто­я­ние равно   км. Ско­рость лодки при дви­же­нии про­тив те­че­ния равна 4 км/ч, при дви­же­нии по те­че­нию равна 8 км/ч. Время, за ко­то­рое лодка до­плывёт от места от­прав­ле­ния до места на­зна­че­ния и об­рат­но, равно   часа. Из усло­вия за­да­чи сле­ду­ет, что это время равно 3 часа. Со­ста­вим урав­не­ние:  . Решив урав­не­ние, по­лу­чим   = 8 . 

Ответ: 8 км.

5. Ту­ри­сты про­плы­ли на лодке от ла­ге­ря не­ко­то­рое рас­сто­я­ние вверх по те­че­нию реки, затем при­ча­ли­ли к бе­ре­гу и, по­гу­ляв 2 часа, вер­ну­лись об­рат­но через 6 часов от на­ча­ла пу­те­ше­ствия. На какое рас­сто­я­ние от ла­ге­ря они от­плы­ли, если ско­рость те­че­ния реки равна 3 км/ч, а соб­ствен­ная ско­рость лодки 6 км/ч?

Ре­ше­ние.

Пусть S км — рас­сто­я­ние, на ко­то­рое от ла­ге­ря от­плы­ли ту­ри­сты. Зная, что ско­рость те­че­ния реки — 3 км/ч, а ско­рость лодки — 6 км/ч, найдём, что время, за ко­то­рое они про­плы­ли туда и об­рат­но, со­став­ля­ет   Учи­ты­вая, что они были на сто­ян­ке 2 часа и вер­ну­лись через 6 часов после от­плы­тия можно со­ста­вить урав­не­ние: 

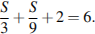
От­сю­да S = 9 км. 

Ответ: 9 км.

6. Катер прошёл от одной при­ста­ни до дру­гой, рас­сто­я­ние между ко­то­ры­ми по реке равно 48 км, сде­лал сто­ян­ку на 20 мин и вер­нул­ся об­рат­но через   после на­ча­ла по­езд­ки. Най­ди­те ско­рость те­че­ния реки, если из­вест­но, что ско­рость ка­те­ра в сто­я­чей воде равна 20 км/ч.

Ре­ше­ние.

Пусть ско­рость те­че­ния реки равна   км/ч. Тогда ско­рость ка­те­ра по те­че­нию реки равна   км/ч, а про­тив те­че­ния —   км/ч. Время дви­же­ния ка­те­ра по те­че­нию реки равно  , а про­тив те­че­ния —   по смыс­лу за­да­чи   Весь путь занял  . Со­ста­вим и решим урав­не­ние:

Тем самым, ско­рость те­че­ния реки равна 4 км/ч. 

Ответ: 4 км/ч.

7. Мо­тор­ная лодка про­шла от одной при­ста­ни до дру­гой, рас­сто­я­ние между ко­то­ры­ми по реке равно 16 км, сде­ла­ла сто­ян­ку на 40 мин и вер­ну­лась об­рат­но через   после на­ча­ла по­езд­ки. Най­ди­те ско­рость те­че­ния реки, если из­вест­но, что ско­рость мо­тор­ной лодки в сто­я­чей воде равна 12 км/ч.

Ре­ше­ние.

Пусть ско­рость те­че­ния реки равна   км/ч. Тогда ско­рость лодки по те­че­нию реки равна  , а про­тив те­че­ния  . Время дви­же­ния лодки от одной при­ста­ни до дру­гой по те­че­нию реки равно  , а про­тив те­че­ния   Весь путь занял   Со­ста­вим урав­не­ние:

Ко­рень −4 не под­хо­дит нам по усло­вию за­да­чи. Ско­рость те­че­ния реки равна 4 км/ч. 

Ответ: 4 км/ч.

8. Теп­ло­ход про­хо­дит по те­че­нию реки до пунк­та на­зна­че­ния 165 км и после сто­ян­ки воз­вра­ща­ет­ся в пункт от­прав­ле­ния. Най­ди­те ско­рость теп­ло­хо­да в не­по­движ­ной воде, если ско­рость те­че­ния равна 4 км/ч, сто­ян­ка длит­ся 5 часов, а в пункт от­прав­ле­ния теп­ло­ход воз­вра­ща­ет­ся через 18 часов после от­плы­тия из него.

Ре­ше­ние. Пусть   км/ч — ско­рость теп­ло­хо­да в не­по­движ­ной воде, тогда   км/ч — ско­рость теп­ло­хо­да по те­че­нию,   км/ч — ско­рость теп­ло­хо­да про­тив те­че­ния. По те­че­нию теп­ло­ход дви­жет­ся   часов, а про­тив те­че­ния  часов, весь путь занял   часов, со­ста­вим урав­не­ние: 

Ко­рень   не под­хо­дит по усло­вию за­да­чи, сле­до­ва­тель­но, ско­рость теп­ло­хо­да равна 26 км/ч. 

Ответ: 26.