Линейные сравнения и системы сравнений. Теория и задачи.
Применения китайской теоремы об остатках.
Сравнения по модулю свойства сравнений.
1) если 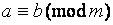 и
и 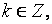 то
то 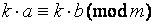 ;
;
2) если 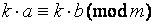 и числа
и числа 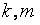 взаимнопросты, то
взаимнопросты, то 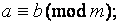
3) если 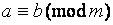 и
и 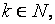 то
то 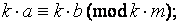
4) если 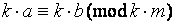 и
и 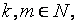 то
то 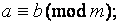
5) если 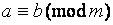 и
и 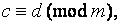 то
то 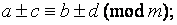
6) если 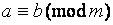 и
и 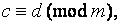 то
то 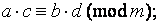
7) если 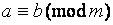 и
и 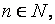 то
то 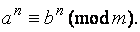
Следствия
1)Любое слагаемое левой или правой части сравнения можно перенести в др часть с противоп зн, т. е., если, напр, 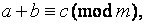 то
то 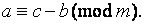
2)В сравнении по модулю 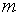 м отбросить или добавить слагаемое, делящееся на число
м отбросить или добавить слагаемое, делящееся на число 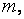 т. е., если, например,
т. е., если, например, 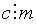 и
и 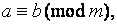 то
то 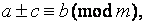 или
или 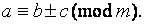
Классом эквивалентности отношения сравнения по данному модулю 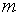 называется класс вычетов по модулю
называется класс вычетов по модулю 
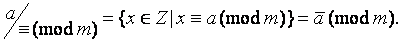
Вычетом класса вычетов по модулю 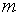 называют любое из чисел, принадлежащих этому классу вычетов.
называют любое из чисел, принадлежащих этому классу вычетов.
Теорема1 (о структуре класса вычетов).
Класс вычетов 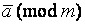 совп с мн-вом чисел вида
совп с мн-вом чисел вида 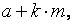 где
где 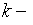 любое нат:
любое нат: 
Теорема 2.Если какой-либо вычет класса вычетов по данному модулю 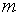 имеет при делении на
имеет при делении на 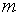 остаток
остаток 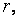 то все числа, входящие в этот класс вычетов, имеют вид
то все числа, входящие в этот класс вычетов, имеют вид 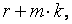 где
где 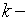 любое целое
любое целое
Суммой 2 классов вычетов 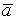 и
и 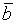 наз класс выч, порожденный эл
наз класс выч, порожденный эл 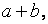 т. е.
т. е. 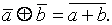
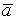 и
и 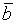 называют класс вычетов, порожденный элементом
называют класс вычетов, порожденный элементом 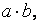 т. е.
т. е. 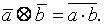
Т1. Алгебра 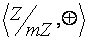 является абелевой группой.
является абелевой группой.
т2. Алгебра 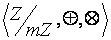 является коммутативным кольцом.
является коммутативным кольцом.
Полной системой вычетов по модулю 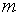 называют мн-во чисел, взятых по одному и только по одному из каждого класса вычетов по данному модулю
называют мн-во чисел, взятых по одному и только по одному из каждого класса вычетов по данному модулю 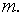
Прим. Полная система вычетов по модулю 6 -это множество: 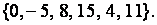
О1. Класс вычетов 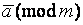 называют взаимно простым с модулем
называют взаимно простым с модулем 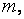 если
если 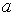 и
и 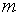 взаимно просты.
взаимно просты.
О2. Приведённой с-мой вычетов по данному модулю 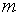 называют множество чисел, взятых по одному и только по одному из каждого класса вычетов по данному модулю
называют множество чисел, взятых по одному и только по одному из каждого класса вычетов по данному модулю 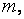 взаимно прост с модулем
взаимно прост с модулем 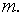
Составим приведенную систему вычетов по модулю 12.Класс вычетов по модулю 12 явл след кл вычетов: 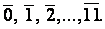 Взаимно простыми с модулем 12 являются следующие классы вычетов:
Взаимно простыми с модулем 12 являются следующие классы вычетов: 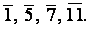 Выберем в каждом из этих классов вычетов по 1 представит:
Выберем в каждом из этих классов вычетов по 1 представит: 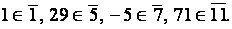
Тогда в кач привед с-мы вычетов по мод 12 м взять мн-во 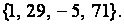
В кольце вычетов по модулю m, обратимыми элементами являются вычеты, взаимно простые с модулем m. Они образуют мультипликативную группу кольца вычетов.
Функцией Эйлера 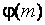 называется число классов вычетов по мод
называется число классов вычетов по мод 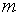 , вз простых с модулем
, вз простых с модулем 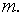
Функция .Эйлера мультипликативна 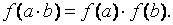
Если число 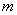 имеет каноническое разложение на простые множители вида,
имеет каноническое разложение на простые множители вида, 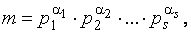 то для вычисления функции Эйлера
то для вычисления функции Эйлера 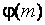 верна ф-ла
верна ф-ла
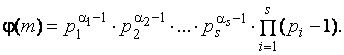
Т (Эйлера). Для любого модуля 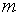 и любого натурального
и любого натурального 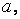 взаимно простого с числом
взаимно простого с числом 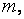 имеет место формула Эйлера:
имеет место формула Эйлера: 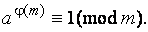
Т (Ферма). Имеют место утверждения.
1. Если натуральное число 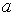 не делится на простое
не делится на простое 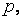 то верно сравнение
то верно сравнение 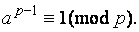
2. Для любого простого модуля 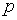 и любого натурального
и любого натурального 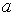 имеет место сравнение
имеет место сравнение 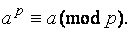
Замечание. Теоремы Эйлера и Ферма часто используют при нахождении остатка от деления больших степеней нат чисел 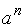 на некоторое натуральное
на некоторое натуральное 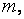 причём числа
причём числа 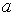 и
и 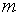 вз просты.
вз просты.
Сформулируем алгоритм решения подобных задач.
1. Вычислить функцию Эйлера 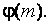
2. Разделить показатель степени 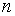 на
на 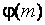 с остатком:
с остатком: 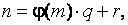 где
где 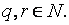
3. Восп св-вами степеней с натуральным показателем и запис выр 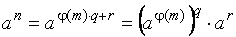 .
.
4. Восп те Эйлера (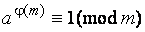 ), запис сравнение
), запис сравнение 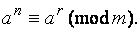
5. Исп оп и св-ва сравн, найти остаток от дел степени 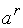 на число
на число 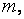 т. е. получить сравнение
т. е. получить сравнение 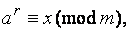 где
где 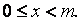 Тогда
Тогда 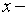 иск ост от деления.
иск ост от деления.
Прим1. Найти остаток от деления числа 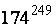 на 13.
на 13.
числа 174 и 13 взаимно просты. .
1. Вычислим зн функции Эйлера от делителя: 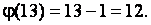
2. Разделим показатель степени 249 на 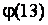 с ост:
с ост: 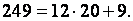
3. По св-вам степеней с нат показателем, имеем цепочку равенств:
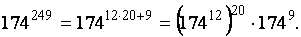
4. По т Эйлера, имеет место сравнение 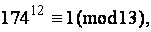 тогда, по св-вам сравнений,
тогда, по св-вам сравнений, 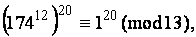 откуда
откуда 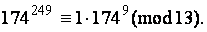
Так как имеет место сравнение 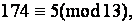 получим:
получим: 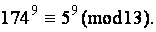
Зам, что 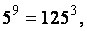 тогда, учит
тогда, учит 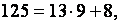 по св-вам сравн получим:
по св-вам сравн получим:
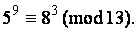 Далее найдём ост от деления
Далее найдём ост от деления 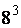 на 13. Для этого поделим число
на 13. Для этого поделим число 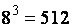 на 13 с ост:
на 13 с ост: 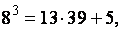 ост= 5. Следовательно, остаток от деления числа
ост= 5. Следовательно, остаток от деления числа 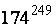 на 13 равен 5.
на 13 равен 5.
Прим2. Доказать, что при любом натуральном n число 37 n+2 +16 n+1 +23 n делится на 7 .
Решение. Очевидно, что 37 є 2(mod 7), 16 є 2(mod 7), 23 є 2(mod 7)
Возведем 1е сравнение в степень n+2 , 2е – в степень n+1 , 3е – в степень n и сложим:
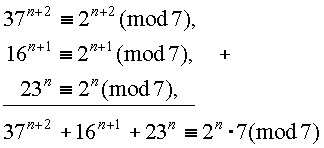 т.е. 37 n+2 +16 n+1 +23 n делится на 7
т.е. 37 n+2 +16 n+1 +23 n делится на 7
Прим3 найти остаток при делении 8 · 541 на 96.
Задачи
1. Докажите, что 3 105 +4 105 делится на 181.
2. Докажите, что число 5 2n-1 Ч 2 n+1 +3 n+1 Ч 2 2n-1 при любом нат n делится на 19 .
3. Найдите остаток от деления числа (9674 6 +28) 15 на 39 .
4. При дел нат числа N на 3 и на 37 получ, соотв, остатки 1 и 33 . Найд ост от дел N на 111 .
5. Док что при любых неч положит зн n число S m =1 n +2 n +3 n +...+m n дел нацело на число 1+2+3+...+m .
6. Докажите, что число 20 15 -1 делится на 11 Ч 31 Ч 61.
7. Докажите, что число p 2 -q 2 , где p и q – простые числа, большие 3, делится на 24 .
8. Док, что если нат число делится на 99, то сумма его цифр в десятич записи не менее 18.
9. Докажите, что если при дел многочлена M(x) с целыми коэфф на х-а в частном получится Q(x) , а в остатке R , то (1-a)S(Q)=S(M)-R , где через S(A) обозн сумма коэфф многочлена А .
10. Докажите, что ни при каких натуральных n и k , k1 , число 3 n k не делится на 5 .
1. Покажите, что по модулю 8 числа −64, −14, 38, −1, 4, 11, 25, −3 сост полную систему вычетов, а числа 17, −11, −33, 19 приведенную систему вычетов.
2. Покажите, что числа 36, −11, −10, 9, −2, 11 составляют полную систему вычетов по модулю 6. Выбрать вычеты, составляющие приведенную систему вычетов по модулю 6.
3. Запишите полную систему вычетов по модулю7, наименьшую по абс величине.
4)Какой остаток будет у след чисел а) б) в)при дел на ч 31?
Для этого нам н знать неск свв из теории чисел, кот покажем на 2 примере 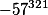
1. 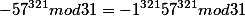 , вынос -1 за "скобки" ( отд множ) и м сразу посч. Если степень числа (321) четн то рез-т =1, если неч то -1.
, вынос -1 за "скобки" ( отд множ) и м сразу посч. Если степень числа (321) четн то рез-т =1, если неч то -1.
2.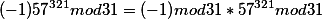
Если число м предст в виде 2 и б сомнож то, ост от этого числа= произв ост от сомнож по этому же модулю.
3.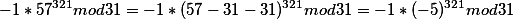
Прибавив или отняв от любого сомнож целое колич модуля - остаток не изменится.
4. 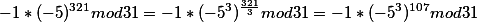
Тоже ничего сложного, просто преобр степень. Обычное свойство степеней.
5. 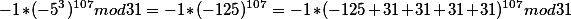
Здесь мы возвели -5 в куб и восп 3 правилом, прибавив к нему 4 раза модуль
6. 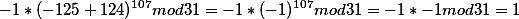
По правилу 1, получим что наш ответ 1 Т е можно утверждать что 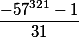 есть целое число.
есть целое число.
7. Последнее правило гласит, что формо, всегда суще два остатка и они равноценны. В нашем прим это 1 и -30, так как 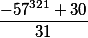 тоже целое .
тоже целое .
Решение сравнения 1 степени
В теории чисел криптографии и других областях науки часто возникает задача отыскать решение сравнения 1 степени вида: 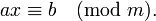 эквивалентно диофантовому уравн ax+my=b
эквивалентно диофантовому уравн ax+my=b
Решение начинают с вычисления НОД(a, m)=d. При этом возможны 2 случая:
Если 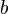 не кратно
не кратно 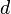 , то у сравнения нет решений.
, то у сравнения нет решений.
Если 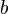 кратно
кратно 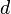 , то у сравнения единственное решение по модулю
, то у сравнения единственное решение по модулю 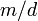 , или, что то же ,
, или, что то же , 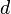 реш по модулю
реш по модулю 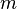 . В этом случае в реультате сокращения исходного сравнения на d получим сравнение :
. В этом случае в реультате сокращения исходного сравнения на d получим сравнение :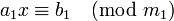
где 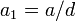 ,
, 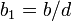 и
и 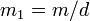 целые числами, причем
целые числами, причем 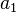 и
и 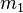 вз просты. Поэтому число
вз просты. Поэтому число 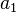 м обр по модулю
м обр по модулю 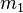 , т е найти такое число c, что
, т е найти такое число c, что 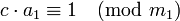 (др сл,
(др сл, 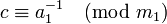 ). Теперь реш находится умножением полученного сравнения на c:
). Теперь реш находится умножением полученного сравнения на c:
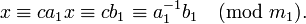
Практически вычисление значения c может быть осуществлено разными способами: с помощью теоремы Эйлера, алг Евклида, теории цепных дробей (см. алгоритм) и др. В частности, теорема Эйлера позволяет записать значение c в виде:
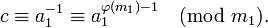
Пусть 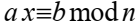
тогда 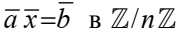
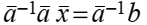
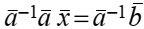
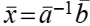
Но 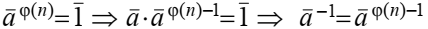
Прим1 Для сравнения 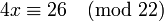 имеем
имеем 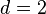 , поэтому по мод 22 сравн имеет 2реш. Замен 26 на 4, сравним с ним по мод 22, и затем сокр все 3 числа на 2:
, поэтому по мод 22 сравн имеет 2реш. Замен 26 на 4, сравним с ним по мод 22, и затем сокр все 3 числа на 2: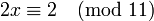
Поск 2 вза просто с модулем 11, то его м обратить по модулю 11 и найти 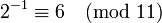 . Умн сравн на 6, получ реш по модулю 11:
. Умн сравн на 6, получ реш по модулю 11: 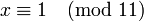 , экв с-ти двух реш по модулю 22:
, экв с-ти двух реш по модулю 22: 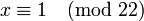 и
и 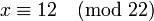 .
.
Прим 2 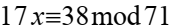
решение 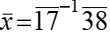
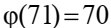
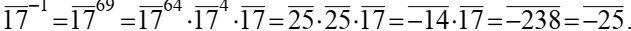
Системы сравнений
Простейшая система сравнений отн попарно вз простых модулей 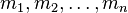
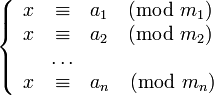
всегда разрешима, и её решение единств по модулю 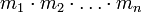 (см. китайскую теорему об остатках).
(см. китайскую теорему об остатках).
Решить следующие системы сравнений в Z: x=2(mod7), x=6(mod 13), x=1(mod3)
полагаем x=7a+2 x=13b+6 x=3c+1 имеем систему диофантовых уравнений
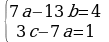 Решаем каждое с помощью расширенного алгоритма Евклида
Решаем каждое с помощью расширенного алгоритма Евклида
1.е уравнение решаем сначала когда правая часть =1 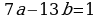 (1) коэф-ты наз большими букв A,B,C:
(1) коэф-ты наз большими букв A,B,C:
A=7 B=13 C=1 (у B изменяем знак чтобы было натуральным, потом изм знак в выходной формуле)
т.к НОД(А,B)=1 C=1 делится на НОД. Задача имеет решение
Вход: m=7 n=13 p=1 q=0 r=0 s=1
1) nm n:=n-m=13-7=6 r:=r-p=0-1=-1 s:=s-q=1-0=1
2)mn m:=m-n=7-6=1 p:=p-r=1-(-1)=2 q:=q-s=0-1=-1
3)m
4)m
5)m
6) m
7) m
8) m=n=1 m:=m-n=1-1=0 p:=p-r=2-(-11)=13 q:=q-s=-1-6=-7
конец X:=r=-11 Y:=s=6
Общее решение (класс) найдем по формулам
Xr=X+B*r/НОД(A,B)=11+(13)*r/1= -11+13r
Yr=Y-Ar/ НОД(A,B) = 6-7r/1= 6 -7r Изменяем знак Yr т.е. положим Yr== -6 +7r
Т.к. правая часть (1) была =1 увеличиваем решения в 4 раза
a=4Xr=4(-11+13r)= -44+52r b=4Yr=4(-6 +7r)=-24+28 r (2)
2)решаем 2-е уравнение 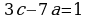
A=3 B=7 C=1 НОД(3,7)=1 С делит НОД
m:=3 n:=7 p=1 q=0 r=0 s=1
1) m
2) m
3) mn m:=m-n=3-1=2 p:=p-r=1-(-2)=3 q:=q-s=0-1=-1
4) mn m:=m-n=2-1=1 p:=p-r=3-(-2)=5 q:=q-s=-1-1=-2
5) m=n m:=m-n=1-1=0 p:=p-r=5-(-2)=7 q:=q-s=-2-1=-3
конец k :=n=1 ; x := r=-2; y := s=1;
Xr=X+B*r/НОД(A,B)=-2+7*r/1= -2+7r
Yr=Y-Ar/ НОД(A,B) = 1-3r/1= 1 -3r
Изменяем знак Yr т.е. положим Yr== -1 +3r Оконч c=-2+7r a=-1+3r (3)
Сравнивая (2) и (3) видим что надо решить еще диофантово уравнение
a= -44+52r1 = -1+3r2 или 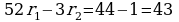
A=52 B=3 C=43 НОД(52,3)=1 С=43 делитcя на НОД=1
mn m=34 n=3 p=1 q=-7 mn m=31 n=3 p=1 q=-8 mn m=28 n=3 p=1 q=-9
mn m=25 n=3 p=1 q=-10 mn m=22 n=3 p=1 q=-11 mn m=19 n=3 p=1 q=-12
mn m=16 n=3 p=1 q=-13 mn m=13 n=3 p=1 q=-14 mn m=10 n=3 p=1 q=-15
mn m=7 n=3 p=1 q=-16 mn m=4 n=3 p=1 q=-17 mn m=1 n=3 r=-1 s=18
mn m=1 n=2 r=-2 s=35 m=n m=1 n=1 p=3 q=-52; конец X:=r=-2 Y:=s=35
Xr=X+B*r/НОД(A,B)=-2+3r Yr=Y-A*r/ НОД(A,B)=35-52r
Т.к. BYr=-35+52r
Так как справа не 1 а 43 умн оба ответа на 43
r1=43Xr=43(-2+3r)= -86+129r r2=43Yr=43(-35+52r)=-1505+2236r
Получим оконч
a= -1+3 r2 =-1+3*(-1505+2236r)=-4516+6708r
b=-24+28r1= -24+28*(-86+129r)= -2432+3612r
c=-2+7r2=-2+7*(-1505+2236r)= -10537+15652 r
-----------------------------------------------------------------------------------------------------------------
2) система уравнений x=4(mod 5), x=1(mod7), x= 1(mod52) ь x=5a+4 x=7b+1 x=52c+1
5a-7b=1-4=-3
Ниже сокращенное изложение прохода адгоритма Евклида
mn m=5 n=7 r=-1 s=1 mn m=5 n=2 p=2 q=-1 mn m=3 n=2 p=3 q=-2
mn m=1 n=2 r=-4 s=3 m=n m=1 n=1 p=7 q=-5 конец X:=r= -4 Y:=s=3
Xr=X+B*r/НОД(A,B)=-4+7r Yr=Y-A*r/ НОД(A,B)=3-5r
BYr Yr=-3+5r Умножим на -3
a=Xr*(-3)=(-3)(-4+7r1)=12-21r1 b=Yr*(-3)=(-3)*(-3+5r1)=9-15r1 (1)
2)5a+4=52c+1 или 5a-52c=-3
mn m=5 n=47 r=-2 s=1 mn m=5 n=42 r=-3 s=1 mn m=5 n=37 r=-4 s=1
mn m=5 n=32 r=-5 s=1 mn m=5 n=27 r=-6 s=1 mn m=5 n=22 r=-7 s=1
mn m=5 n=17 r=-8 s=1 mn m=5 n=12 r=-9 s=1 mn m=5 n=7 r=-10 s=1
mn m=5 n=2 p=11 q=-1 mn m=3 n=2 p=21 q=-2 mn m=1 n=2 r=-31 s=3
m=n m=1 n=1 p=52 q=-5
конец X:=r= -31 Y:=s=3
Xr=X+B*r/НОД(A,B)=-31+52r Yr=Y-A*r/ НОД(A,B)=3-5r
BYr Yr=-3+5r Умножим на -3
a=Xr(-3)=Xr*(-31+52r2)=93-156r2 c=Yr*(-3)=(-3)*(-3+5r2)=9-15r2 (2)
Из 1 и 2 приравнивая a – 3-е уравн a=12-21r1 = 93-156r2 или -21r1+156r2 =93-12=81
Сокращаем на 3 -7r1+52r2=27
mn m=7 n=52 r=-1 s=1 mn m=7 n=45 r=-2 s=1 mn m=7 n=38 r=-3 s=1 mn m=7 n=31 r=-4 s=1
mn m=7 n=24 r=-5 s=1 mn m=7 n=17 r=-6 s=1 mn m=7 n=10 r=-7 s=1 mn m=7 n=3 p=8 q=-1
mn m=4 n=3 p=15 q=-2 mn m=1 n=3 r=-22 s=3 mn m=1 n=2 r=-37 s=5 m=n m=1 n=1 p=52 q=-7
Результат: r1=999-1404r r2=135-189r Оконч из ф-л (1),(2):
a=12-21r1=12-21*(999-1404r)=-21966+29484r
b=9-15r1=9-15*(999-1404r)=-14976+21060r
c=9-15r2 =9-15*(135-189r)=-2016+25515r
Китайская теорема об остатках
Ф1) Пусть числа 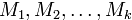 — попарно взаимно простые, и
— попарно взаимно простые, и 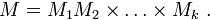
Тогда система 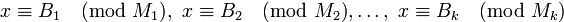
имеет единственное решение среди чисел 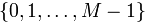 , и это решение может быть представлено в одном из следующих видов:
, и это решение может быть представлено в одном из следующих видов:
1. либо 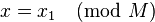 при
при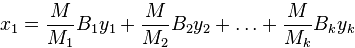
и 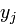 обозначим число, обратное числу
обозначим число, обратное числу 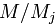 относительно умножения по модулю
относительно умножения по модулю 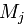 :
: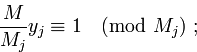
2. либо 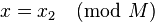 при
при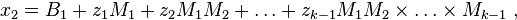
и числа х 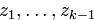 последоват определяемых из сравнений
последоват определяемых из сравнений
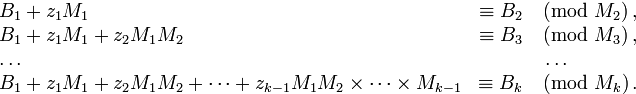
Ф2)пусть m = m1 m2 ... mk.
Тогда кольцо вычетов по модулю m изоморфно прямой сумме (или прямому произведению) колец вычетов Zmi: Zm ≅ Zm1 ⊕ Zm2 ⊕ ... ⊕ Zmk
При всей своей простоте Китайская теорема об остатках очень важна, т к позволяет свести изучение кольца вычетов по модулю m, где m — произвольное целое, к изучению колец вычетов по модулю ps, где p — простое число. Действ, любое целое число представимо в виде m = m1 m2 ... mk, где каждое из чисел mi есть степень простого числа. Тогда Zm изоморфно прямой сумме колец Zmi (примарных колец)
Обобщение китайской теоремы об остатках
Т1 Система 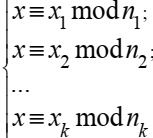 (1)
(1)
совместна тогда и только тогда, когда 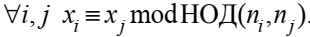
Т2 Если система (1) совместна, то при любом частном решении 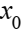 ее общее решение имеет вид
ее общее решение имеет вид
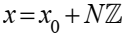 где
где 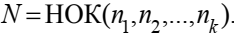
Примеры рещения систем сравнений
1) решить систему сравнений 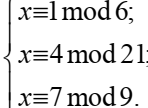
Решение их 1) 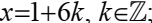 из 2)
из 2) 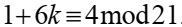 т е
т е
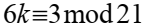
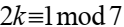 и значит
и значит 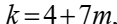 тогда
тогда 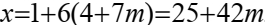 Подставим в 3)
Подставим в 3) 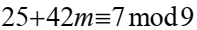 откуда
откуда 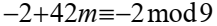
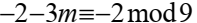
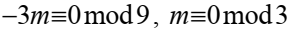
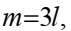
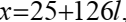 Заметим, что
Заметим, что 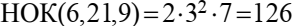
2)Найти решение системы сравнений
x=2(mod 5),
x=15(mod 17),
x=5(mod 12).
Решение Числа 5, 17 и 12 - взаимно простые, по теореме решение существует.
Вычислим вел 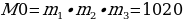 , Mi=M0/mi, i=1,...,n, M1=204, M2=60, M3=85.
, Mi=M0/mi, i=1,...,n, M1=204, M2=60, M3=85.
Решим вспомогательные сравнения Miyi=ai(mod mi), i=1,...,3.
Рассмотрим 1е сравнение:
204y1=2(mod 5)=200y1+4y1=2(mod 5)=0+4y1=2(mod 5).
Здесь учли, что 200y1(mod 5)=0, т.к. 200 делится на 5.
Перебираем y1=1,2,3,4,5 в сравн 4y1=2(mod 5), нах y1=3. Действ, 4·3-2=12-2=10 дел на 5.
Аналогично находим решения 60y2=15(mod 17), y2=13, 85y3=5(mod 12), y3=5.
Получаем решение
x=M1y1+M2y2+M3y3 (mod M0)=1817(mod 1020)=797(mod 1020)
Примеры решений з-ч
1) Найти натуральное число, которое при делении на 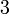 дает в остатке
дает в остатке 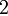 , при делении на
, при делении на 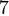 дает в остатке
дает в остатке 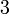 , а при делении на
, а при делении на 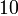 — в ост
— в ост 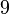 .
.
Реш. Пусть 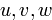 — частные от деления неизв числа на
— частные от деления неизв числа на 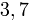 и
и 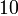 соотв. Имеем:
соотв. Имеем:
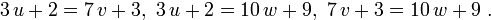
Решаем последнее уравнение в целых числах,
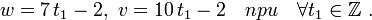
Подст найденное выражение для 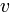 в 1 уравнение
в 1 уравнение 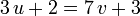 :
: 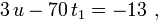
кот также м решить: 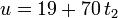 при
при 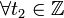 . След общий вид искомых чисел:
. След общий вид искомых чисел:
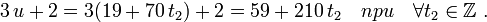
Наименьшее положительное число получается при 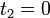 .Ответ.
.Ответ. 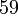 .
.
прим2) Решим систему сравнений
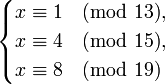
\Реш Так как модули 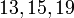 попарно взаимно просты, то данная система имеет единств решение по модулю
попарно взаимно просты, то данная система имеет единств решение по модулю 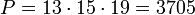 . Сравнение
. Сравнение 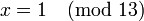 соответствует диофантовому уравнению
соответствует диофантовому уравнению 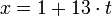 , где
, где 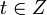 .
.
Заменяя 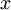 во в2 сравнении системы на
во в2 сравнении системы на 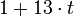 , получаем
, получаем 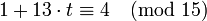 , т.е.
, т.е.  .
.
К числу 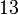 обратным мультипликативным элементом по модулю
обратным мультипликативным элементом по модулю 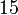 является число
является число 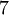 . Умн посл сравн на
. Умн посл сравн на 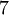 и переходя в нём к вычетам по мод 15, получим
и переходя в нём к вычетам по мод 15, получим 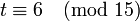 . Таким обра,
. Таким обра, 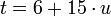 , где
, где 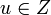 .
.
Следовательно, 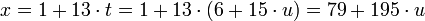 , при этом все числа вида
, при этом все числа вида 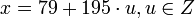 являются решениями первых двух сравнений данной системы. Подставим в 3 сравнение вместо
являются решениями первых двух сравнений данной системы. Подставим в 3 сравнение вместо 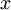 полученное выше значение
полученное выше значение 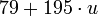 :
:
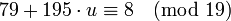 ,или (переносим
,или (переносим 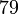 )
)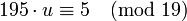 ,
,
далее (делим обе части на 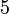 )
)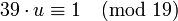 .
.
Так как 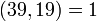 , то
, то 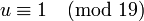 , или
, или 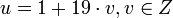 .Итак,
.Итак,
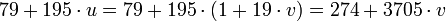 , т.е.
, т.е. 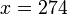 .
.
Пример на применение Китайской теоремы об остатках.
Пусть m = 3·5·7 = 105. Ск кв корней из единицы в Zm?
Реш: 23 = 8 корней. При представлении Z105 в виде прямой суммы Z3⊕Z5⊕Z7 они соответствуют тройкам (1, 1, 1) (1, 1, -1) (1, -1, 1) (1, -1, -1) (-1, 1, 1) (-1, 1, -1) (-1, -1, 1) (-1, -1, -1),
каждая координата которых равна ±1. Чтобы найти конкретные числа, надо применить алгоритм из Китайской теореме об остатка (видимо, его след бы наз "Китайский алгоритм", но такое название не является общепринятым).
Список литературы
1) Виноградов И.М. Основы теории чисел изд. Лань, 2009г
2) Н. Б. Алфутова, А. В. Устинов Алгебра и теория чисел для математических школ
3) Сравнения.doc https://studfiles.net/preview/5358203/page:2/
4)Б.М.Веретенников, И.М.Михалёва, Алгебра и теория чисел ч.1., УФУ , Екатеринбург, 2014г.
4) ВАЛИЦКАС А.И. ИЗБРАННЫЕ ВОПРОСЫ ТЕОРИИ ЧИСЕЛ И КОМБИНАТОРНОГО АНАЛИЗА, ФГБУ ,ТиМОМ, Тобольск 2011







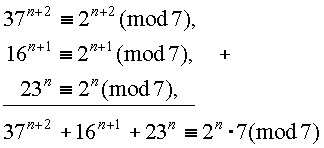 т.е. 37 n+2 +16 n+1 +23 n делится на 7
т.е. 37 n+2 +16 n+1 +23 n делится на 7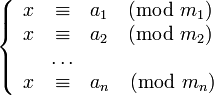
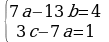 Решаем каждое с помощью расширенного алгоритма Евклида
Решаем каждое с помощью расширенного алгоритма Евклида 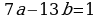 (1) коэф-ты наз большими букв A,B,C:
(1) коэф-ты наз большими букв A,B,C: 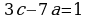
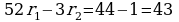
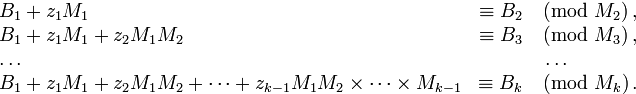
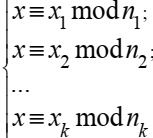 (1)
(1)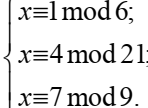
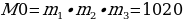 , Mi=M0/mi, i=1,...,n, M1=204, M2=60, M3=85.
, Mi=M0/mi, i=1,...,n, M1=204, M2=60, M3=85.