Задачи на проценты

Муниципальное бюджетное образовательное учреждение Краснинская средняя общеобразовательная школа

Задачи на проценты

Работу выполнил Большунов Андрей

7 а класс

Руководитель: Серова Надежда Николаевна

Красный 2015

• Моя цель : систематизировать свои знания о задачах на проценты.

• Задачи:

• Изучить литературу и подкорректировать свои знания о процентах
• Проверить свои умения решать задачи на проценты
• Ответить на вопросы:

Нужны ли мне знания о процентах?

Как часто мы встречаемся с процентами?

• Методы исследования

• Анализ математической литературы по теме исследования
• Изучение, исследование и сбор информации
• Решение задач по теме

• Гипотеза:

«У меня хватит знаний, чтобы решать задачи на проценты из ГИА»

План:

• Введение. Проценты в прошлом и настоящем.
• Основная часть:

• Три основных действия.
• Основные типы задач на проценты.
• Процентные вычисления в жизненных ситуациях

а). Распродажа, тарифы, штрафы. Примеры задач.

4) Задачи на смеси, растворы, сплавы.

• Примеры задач, взятых из ГИА прошлых лет.

• Вывод.

Немного истории

• Процент - это одна сотая часть целого.

Слово «процент» происходит от латинских слов pro centum , что

буквально означает «со ста».

Проценты дают возможность легко сравнивать между собой части

целого, упрощают расчёты и поэтому очень распространены.

Широко начали использовать проценты в Древнем, Риме, но идея

процентов возникла раньше – вавилонские ростовщики уже умели

находить проценты. Были известны проценты и в Индии.

Долгое время под процентами понимались исключительно прибыль или убыток на каждые 100 рублей.

Знак % произошёл благодаря опечатке. В рукописях pro centum

часто заменяли словом « cento » (сто) и писали его сокращенно- cto. В Париже в 1685 году была напечатана книга-руководство по

коммерческой арифметике, где по ошибке наборщик вместо cto

набрал %.

После этой ошибки многие математики стали употреблять знак %

для обозначения процентов , и постепенно он получил всеобщее

признание. Но существуют и другие версии возникновения этого знака.

Проценты в прошлом и настоящем

Проценты - одно из математических понятий, которые часто

встречаются в повседневной жизни. Мы часто слышим или читаем, что, например, в выборах приняли участие 52,5% избирателей, промышленное производство сократилось на 12%, банк начисляет 14% годовых, молоко содержит 3,2% жира и т.д.

Долгое время проценты применялись только в торговых и

денежных сделках. Со временем область применения расширилась, проценты встречаются в хозяйственных и финансовых расчётах, статистике, науке и технике.

С помощью процентов часто показывают изменение той или иной конкретной величины. Такая форма является наглядной числовой характеристикой изменения, характеризующей значимость произошедшего изменения.

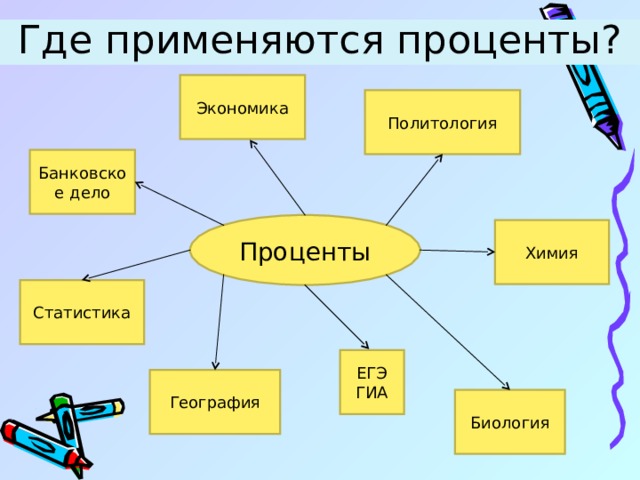
Где применяются проценты?

Экономика

Политология

Банковское дело

Проценты

Химия

Статистика

ЕГЭ

ГИА

География

Биология

Основные действия, связанные с процентами.

• Нахождение процента от числа.

Чтобы найти а% от b , надо b ∙ 0,01a

• Нахождение числа по его процентам.

Если известно, что а % числа х равно b , то х = b : 0,01а.

• Нахождение процентного отношения чисел.

Чтобы найти процентное отношение чисел, надо отношение этих чисел умножить на 100%

a : b ∙ 100%

Нахождение процента от числа

Задача 1. Огород занимает 8 га. Картофелем занято 45% площади этого огорода. Сколько гектаров занято картофелем?

Решение:

45%=0,45 , 8га ∙ 0,45=3,6га – занято картофелем

Ответ: 3,6 га

Нахождение процента от числа

Задача 2. Клиент внёс 3000 р. на два вклада, один из которых даёт годовой доход, равный 8%, а другой – 10%.Через год на двух счетах у него было 3260 р. Какую сумму клиент внёс на каждый вклад?

Решение : Пусть на один счёт клиент внёс х рублей, тогда годовой доход составит 0,08х руб. , а на второй счёт – у рублей и годовой доход составил 0,1у рублей, тогда

1,08х +3300-1,1х=3260

х=2000

у=3000-2000=1000 руб.

Ответ :1000 рублей на один вклад, 2000 рублей на другой.

Нахождение числа по проценту

Задача 1. Увеличив производительность труда на 7 %, рабочий сделал за этот же срок на 98 деталей больше, чем намечалось по плану. Сколько деталей рабочий должен был сделать по плану?

Решение: 7%=0,07, 98 : 0,07=1400 деталей должен был сделать по плану.

Ответ :1400 деталей

Нахождение числа по проценту

Задача 2. Свежие грибы содержат 92% воды, а сухие -8%. Сколько получится сухих грибов из 23кг свежих?

Решение: Грибы в любой степени влажности состоят из воды и абсолютно сухого вещества, которое в данной порции грибов неизменно. В свежих грибах этого вещества 8%, а в сухих- 92%.Если искомая величина х, то 0,92х=0,08 ∙ 23 ,

0,92x = 1,84 х=2

Ответ : 2кг сухих грибов .

Задачи на процентное отношение

Задача1 . В растворе соли массой 200 г содержится 28 г соли. Какой процент от массы раствора составляет масса соли?

Решение : 28 : 200 ∙ 100% =14%

Ответ : 14%

Задача 2 . В классе 25 учащихся.4 ученика написали контрольную работа на отличную отметку. Какой процент от класса это составляет?

Решение : 4 : 25 ∙ 100% = 16%

Ответ : 16%

Основные типы задач

Одна величина больше(меньше) другой на р %.

• Если а больше b на р %, то а = b + 0,01р b =

= b (1+0,01р).

2) Если а меньше b на р %, то а= b -0,01р b =

=b (1-0,01р).

Пример: Число 72 уменьшили на 20%:

72 – 72∙ 0,02=57,6,

Также получится, если вычислять по формуле

72 (1 – 0,01 ∙ 20) = 72 ∙ 0,8 = 57,6

Основные типы задач

Одна величина больше(меньше) другой на р %.

3) Если увеличили число а на р %, а затем

уменьшили на р%, то а(1+0,01р) цена после увеличения; а(1+0,01р)(1-0,01р)= а(1-(0,01р) 2 ). (*) новая цена

Пример. Цену товара снизили на 30%, затем новую цену повысили на 30%. Как изменилась цена товара?

Решение: Пусть а – первоначальная цена товара, тогда:

0,7а-цена товара после снижения; 0,7а+0,7а ∙ 0,3=0,91а новая цена. Снизилась на 0,09а, т.е. на 9%.

Это же получим используя формулу (*): а(1 – )=0,91а Цена снизилась на 9%

Ответ: цена снизилась на 9%.

Процентные вычисления в жизненных ситуациях.

Скидка, распродажа, тарифы, штрафы, бюджет, пеня- слова нашей реальной жизни. Их мы можем встретить в газетах, журналах, документах, слышать по телевизору и радио. Поэтому очень важно уметь применять свои знания процентов в жизненных ситуациях.

Примеры задач, сюжеты которых взяты из реальной жизни

Задача 1 (распродажа). Зонт стоил 360р. В ноябре цена зонта была снижена на 15%, а в декабре ещё на 10%. Какой стала стоимость зонта в декабре?

Решение:

Стоимость зонта в ноябре составила 85% от 360р., т.е. 306р. Второе снижение происходило по отношению к новой цене зонта; теперь найду 90% от 306р., т.е. 275,4р.

Ответ: 275р. 40к.

Примеры задач, сюжеты которых взяты из реальной жизни

Задача 2 (Бюджет. Зарплата.): При приёме на работу директор предприятия предлагает зарплату 6200 р. Какую сумму получит рабочий после удержания налога на доходы физических лиц?

Замечание: При начислении налога на доходы физических лиц учитывается стандартный вычет 400 р., налог составляет 13% от оставшейся суммы.

Решение:

1) (6200-400) 0,13=754 р. - составит налог.

2) 6200-754=5446 р. –получит рабочий.

Ответ:544 6 р. зарплата рабочего.

Примеры задач, сюжеты которых взяты из реальной жизни

Задача 3(Штрафы.). Занятия ребёнка в музыкальной школе родители оплачивают в сбербанке, внося ежемесячно 250 р. Оплата должна производиться до 15 каждого месяца, после чего за каждый просроченный день начисляется пеня в размере 4% от суммы оплаты занятий за один месяц. Сколько придётся платить родителям , если они просрочат оплату на неделю?

Решение: Так как 4% от 250 р. составляют 10 р., то за каждый просроченный день сумма оплаты будет увеличиваться на 10 р. Если родители просрочат оплату на день то им придётся заплатить 260 р., а если на неделю 250+7 ∙ 10=320 (р.)

Ответ: 320 р.

Задачи на смеси

Задачи на смеси, растворы, сплавы называют ещё задачами на процентное содержание или концентрацию. Смесь(твёрдая, жидкая, газообразная, сыпучая) состоит из основного вещества и примеси. Всякая смесь или сплав характеризуется концентрацией – процентным содержанием какого-то равномерно распределённого в смеси вещества. Для того, чтобы рассчитать концентрацию смеси(раствора, сплава) обычно используют формулу: n=m в /m р ,

где n - концентрация, m в - масса вещества в растворе (сплаве), m р -масса раствора (сплава).

Задачи на смеси широко применяются химиками.

Под понятие концентрации подходит жирность

(молока), влажность(грибов), крепость(водно-спиртовых смесей) и т.д.

Задачи на смеси

Задача 1. Сколько граммов воды надо добавить к 180 г сиропа, содержащего 25% сахара , чтобы получить сироп, концентрация которого равна 20%?

Решение : Пусть надо добавить х г воды, тогда

0,2(180+х)=0,25 ∙ 180 ,

х=45

Ответ: 45 г воды.

Задачи на смеси

Зада ч а 2. Сколько граммов 15%-ного раствора соли надо добавить к 50г 60%-ного раствора соли, чтобы получить 40%-ный раствор соли?

Решение : Пусть надо добавить х г 15%-ного раствора соли, тогда в 50 г 60%-ного раствора соли содержится 30 г соли, в х г 15%-ного раствора соли- 0,15х г., получаем уравнение

0,15х+30=0,4(50+х)

х=40

Ответ :40 г 15%-ного раствора соли надо добавить.

Задачи на смеси

Зада ч а 3 . Сплав состоит из меди, цинка и свинца. Медь составляет 54% сплава, а цинк – 26% сплава. Сколько меди и цинка входит в сплав, содержащий 0,8 кг свинца?

Решение : 100% - (54% + 26%)=20% сплава составляет свинец,

0,8 : 0,2 = 4(кг) масса всего сплава.

0,54 ∙ 4 = 2,16(кг) масса меди в сплаве,

0,26 ∙ 4 = 1,04(кг) масса цинка в сплаве

Ответ : 2,16 кг меди и 1,04 кг цинка в сплаве.

Задачи из ГИА - 2014

Зада ч а 1. Наценка книжного магазина составляет 20% к оптовой цене товара. В магазине проводится акция, по которой школьникам предоставляется скидка 5% от розничной цены. Сколько рублей заплатит семиклассник Миша за книгу, если её оптовая цена – 150 рублей?

Решение: 150 + 0,2 ∙ 150 = 180 (р.) розничная цена.

180 – 0,05 ∙ 180 = 180 – 9 = 171 (р.) заплатит Миша.

Ответ: 171 рубль.

Задачи из ГИА - 2014

Зада ч а 2. Шоколадка, которая стоила 45 рублей, продается с 15%-й скидкой. При покупке шести таких шоколадок покупатель отдал 500 рублей. Сколько рублей сдачи он должен получить?

Решение: 45 – 0,15 ∙ 45 = 45 – 6,75 = 38,25(р) цена шоколадки со скидкой.

500 – 6 ∙ 38,25 = 500 – 229,5 = 270,5 (р) сдача

Ответ: 270,5 рублей

Задачи из ГИА - 2014

Зада ч а 3. Грузовик вместимостью 5 тонн может увезти 3,6% кирпичей, прибывших на железнодорожную станцию в грузовом контейнере. Сколько процентов кирпичей могут увезти три грузовика вместимостью по 4 тонны каждый?

Решение: 5 : 0, 036 = 5000/36 (т) масса всех кирпичей в грузовом контейнере.

3 ∙ 4=12(т) вместимость трех грузовиков.

12 : 5000/36 ∙ 100%= 12 ∙ 36/5000 ∙ 100% =

= 12 ∙ 36 ∙ 2 : 100 % = 8,64%.

Ответ: 8,64%

Вывод

Какую бы область человеческой жизни мы не затрагивали, в этой области обязательно находилась проблема или задача, решаемая с помощью процентов.

Знание ­ великая сила.

Вывод

Теперь я знаю, что в современном мире прожить без знаний процентов невозможно. Чтобы быть хорошим специалистом, уметь разбираться в большом потоке информации, необходимо знать проценты.

Я повторил, систематизировал и углубил свои знания о процентах.

Я умею решать многие задачи на проценты, но далеко не все, это задача следующего года.

Я доволен своей работой. Я могу решать задачи на проценты из ГИА.

Моя гипотеза подтвердилась

Спасибо за внимание!

Список используемой литературы

• А.В. Шевкин. Текстовые задачи в школьном курсе математике. Педагогический университет «Первое сентября», 2006.
• Учебник Математика – 6 класс, Н.И. Зубарева, Л.Г. Мордкович, Мнемозина, 2005 год.
• Учебник Математика – 6 класс, Г. В. Дорофеев, Л.Г. Петерсон, М., Баласс, « С- инфо», 1998г.
• Газета Математика, № 4, 2006год. Издательский дом « Первое сентября».

• Сайт учителя математики.[Электронный ресурс] – Режим доступа: http://le-savchen.ucoz.ru/publ/1-1-0-31 свободный