Проценты
Знакомство учащихся с текстом задач и выделение основных компонентов в них.
Таблица для решения задач имеет следующий вид:
| Наименование веществ, растворов, смесей, сплавов | % содержание вещества (доля содержания вещества) | Масса раствора (смеси, сплава) | Масса вещества |
| | | | |
Решение задач.
Рассмотрим решения задач с применением таблицы.
Задача 1. В сосуд содержащий 2 кг 80 % -го водного раствора уксуса добавили 3 кг воды. Найдите концентрацию получившегося раствора уксусной кислоты.
Решение.
| Наименование веществ, смесей | % содержание (доля) вещества | Масса раствора(кг) | Масса вещества (кг) |
| Исходный раствор | 80 % = 0,8 | 2 | 0,8·2 |
| Вода | - | 3 | - |
| Новый раствор | х % = 0,01х | 5 | 0,01х·5 |
Масса уксусной кислоты не изменилась, тогда получаем уравнение:
0,01х·5 = 0,8·2
0,05х = 1,6
х = 1,6:0,05
х = 32
Ответ: концентрация получившегося раствора уксусной кислоты равна 32 %.
Задача 2.Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?
Решение.
| Наименование веществ, смесей | % содержание (доля) вещества | Масса раствора (г) | Масса вещества (г) |
| Исходный раствор | 70 % = 0,7 | 200 | 0,7·200 |
| Вода | - | х | - |
| Новый раствор | 8 % = 0,08 | 200 + х | 0,08(200 + х) |
Анализируя таблицу, составляем уравнение :
0,08(200 + х) = 0,7·200
16 + 0,08х = 140
0,08х = 124
х = 1550
Ответ:1,55 кг воды.
Задача 3. Смешали некоторое количество 12% раствора соляной кислоты с таким же количеством 20 % раствора этой же кислоты. Найти концентрацию получившейся соляной кислоты.
Решение.
| Наименование веществ, смесей | % содержание (доля) вещества | Масса раствора (кг) | Масса вещества (кг) |
| I раствор | 12 % = 0,12 | у | 0,12у |
| II раствор | 20 % = 0,2 | у | 0,2у |
| Смесь | х % = 0,01х | 2у | 0,01х·2у |
Анализируя таблицу, составляем уравнение :
0,12у + 0,2у = 0,01х·2у
Получили уравнение с двумя переменными, учитывая, что  , имеем
, имеем
0,32 = 0,02х
х = 16
Ответ: концентрация раствора 16 %.
Задача 4. Смешали 8кг 18 % раствора некоторого вещества с 12 кг 8 % раствора этого же вещества. Найдите концентрацию получившегося раствора.
Решение.
| Наименование веществ, смесей | % содержание (доля) вещества | Масса раствора (кг) | Масса вещества (кг) |
| I раствор | 18 % = 0,18 | 8 | 0,18·8 |
| II раствор | 8 % = 0,08 | 12 | 0,08·12 |
| Смесь | х % = 0,01х | 20 | 0,01х·20 |
Уравнение для решения задачи имеет вид:
0,01х·20 = 0,18·8 + 0,08·12
0,2х = 2,4
х = 12
Ответ: концентрация раствора 12 %.
Задача 5. Смешав 40 % и 15 % растворы кислоты, добавили 3 кг чистой воды и получили 20 % раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80 % раствора той же кислоты, то получили бы 50 %-ый раствор кислоты. Сколько килограммов 40 % -го и 15 % растворов кислоты было смешано?
Решение.
| Наименование веществ, смесей | % содержание (доля) вещества | Масса раствора (кг) | Масса вещества (кг) |
| I раствор | 40 % = 0,4 | х | 0,4х |
| II раствор | 15 % = 0,15 | у | 0,15у |
| Вода | - | 3 | - |
| Смесь I | 20 % = 0,2 | х + у +3 | 0,2(х + у +3) |
Получаем уравнение:0,4х + 0,15у = 0,2(х + у +3)
Выполним вторую операцию:
| I раствор | 40 % = 0,4 | х | 0,4х |
| II раствор | 15 % = 0,15 | у | 0,15у |
| Кислота | 80 % = 0,8 | 3 | 0,8·3 |
| Смесь II | 50 % = 0,5 | х + у +3 | 0,5(х + у +3) |
Итак, 0,4х + 0,15у + 0,8·3 = 0,5(х + у +3).
Для решения задачи получаем систему уравнений:
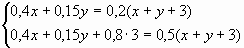
Решаем систему уравнений:
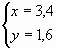
Ответ:3,4 кг 40 % кислоты и 1,6 кг 15 % кислоты.
Задача 6. Имеется три сосуда. В первый сосуд налили 4 кг 70 % сахарного сиропа, а во второй – 6 кг 40 % сахарного сиропа. Если содержимое первого сосуда смешать с содержимым третьего сосуда, то получим в смеси 55 % содержание сахара, а если содержимое второго сосуда смешать с третьим, то получим 35 % содержание сахара. Найдите массу сахарного в третьем сосуде сиропа и концентрацию сахара в нем.
Решение.
| Наименование веществ, смесей | % содержание (доля) вещества | Масса раствора (кг) | Масса вещества (кг) |
| I сосуд | 70 % = 0,7 | 4 | 0,7·4=2,8 |
| II сосуд | 40 % = 0,4 | 6 | 0,4·6 = 2,4 |
| III сосуд | у % = 0,01у | х | 0,01ху |
| I и III сосуды | 55 % = 0,55 | 4+х | 0,55(4+х) или 2,8+0,01ху |
| II и III сосуды | 35 % = 0,35 | 6+х | 0,35(6+х) или 2,4+0,01ху |
Итак, получаем систему уравнений :
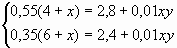
Решаем её:
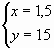
Ответ:1,5 кг сахарного сиропа 15 % концентрации.
6

















