Задачи на сечения

Задачи на построение сечений

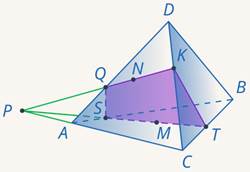
Задача 8. Построить сечение тетраэдра по трем точкам (см. рис. 20).

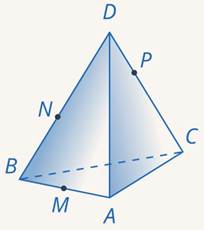
Рис. 20. Иллюстрация к задаче 8

Решение

Чтобы построить сечение, нужно изобразить отрезки, по которым секущая плоскость пересекает грани. На левой грани мы имеем уже две точки, значит, знаем и сам отрезок. Соединяем точки. Аналогично на задней грани (см. рис. 21).

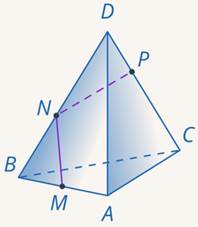
Рис. 21. Иллюстрация к задаче 8

Редко когда в задаче у нас будут сразу две точки на каждой необходимой грани. Чтобы построить сечение, нужно будет выходить за пределы самих граней. Суть метода построения сечений состоит в том, чтобы находить отрезки на чертеже, лежащие в одной плоскости, пересекать их, получая дополнительные точки плоскости сечения.

В нашем случае легко видеть, что отрезк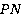и   и 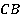  лежат в одной плоскости задней грани.

Продлим их и найдем точку пересечения 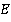  (см. рис. 22).

Рис. 22. Иллюстрация к задаче 8

Точка 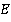  лежит в плоскости сечения и нижней грани. Точка  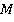 тоже. Значит, мы можем простроить след плоскости сечения в нижней грани. Получим еще одну точку  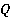 (см. рис. 23).

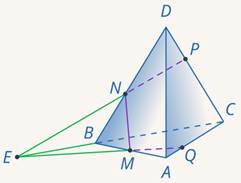
Рис. 23. Иллюстрация к задаче 8

Осталось соединить 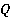  и 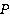 . Мы построили сечение (см. рис. 24).

Рис. 24. Иллюстрация к задаче 8

Такой метод построения часто так и называют – метод следов. Главное, всегда оценивать, лежат ли данные прямые в одной плоскости. Частая ошибка, когда скрещивающиеся прямые на чертеже принимают за пересекающиеся.

Задача 9. Построить сечение параллелепипеда плоскостью   (см. рис. 25).

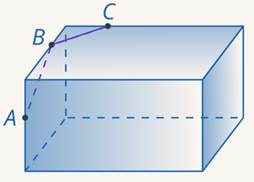
Рис. 25. Иллюстрация к задаче 9

Решение

Итак, два отрезка у нас уже есть – это 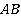  и 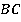 . Чаще всего новые точки ищут в плоскости нижнего основания, но это не обязательно, просто так легче изображать. Продолжим отрезок  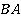 и левое нижнее ребро до пересечения. Обозначим эту точку как  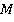 (см. рис. 26). Она у нас пока единственная точка следа от плоскости сечения в нижнем основании. Но след можно построить либо по двум точкам, либо по одной, если есть прямая, параллельная нашему следу.

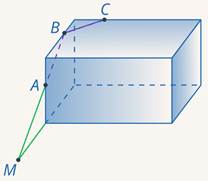
Рис. 26. Иллюстрация к задаче 9

Теперь вспомним, что если плоскость пересекает две параллельные плоскости, то она оставляет на них параллельные следы. Таким образом, след в нижнем основании нужно проводить параллельно следу в верхнем основании. Проведем через 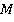  прямую в плоскости нижнего основания параллельно отрезку  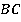. Мы получили еще две точки –  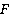 и   (см. рис. 27).

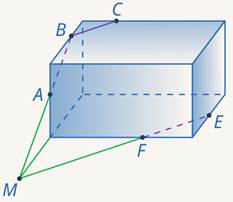
Рис. 27. Иллюстрация к задаче 9

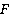Соединяем   и  ,   и 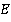  (см. рис. 28).

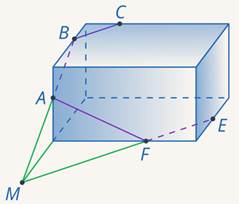
Рис. 28. Иллюстрация к задаче 9

В правой грани через точку 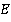  проводим прямую, параллельную следу в левой грани. Получили последнюю необходимую точку  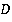 (см. рис. 29).

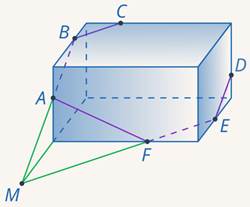
Рис. 29. Иллюстрация к задаче 9

Построим сечение (см. рис. 30).

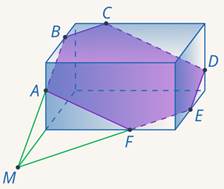
Рис. 30. Иллюстрация к задаче 9

Задача 10. Построить сечение параллелепипеда по трем точкам (см. рис. 31).

Рис. 31. Иллюстрация к задаче 10

Решение

Итак, мы можем соединить точк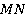и   и 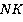  (см. рис. 32).

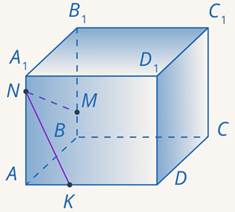
Рис. 32. Иллюстрация к задаче 10

Далее у нас есть два варианта. Мы можем пересечь прямые 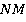  и 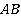 . Полученная точка лежит в плоскости нижней грани. Осталось соединить ее с точкой  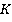 (см. рис. 33).

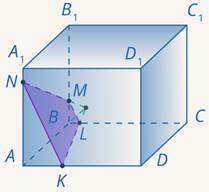
Рис. 33. Иллюстрация к задаче 10

Либо можно было сразу в плоскости задней граней через точку 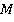  провести отрезок параллельно отрезку  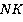 (см. рис. 34).

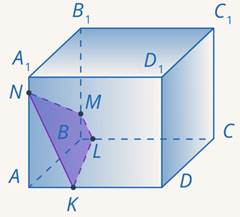
Рис. 34. Иллюстрация к задаче 10

Если точки на ребрах, задающие плоскость сечения, немного сместить, то сечение может выглядеть иначе (см. рис. 35).

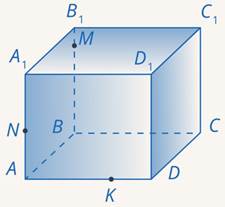
Рис. 35. Иллюстрация к задаче 10

Соединим точк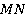и   и 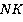 . Продлим  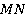 и 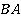  до пересечения в точке  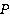. Эта точка лежит в плоскости нижней грани. Соединяем ее с  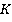. Получили точку  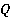 (см. рис. 36).

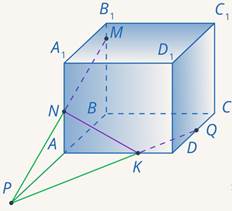
Рис. 36. Иллюстрация к задаче 10

В плоскости задней грани через точку 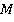  проводим прямую параллельно  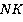. Получили точку  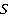. Сечение построено (см. рис. 37).

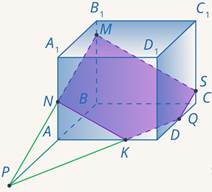
Рис. 37. Иллюстрация к задаче 10

Здесь можно было обойтись и без дополнительной точки 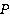 .Через  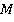 проводим прямую параллельно  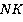. Получили точку  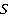 (см. рис. 38).

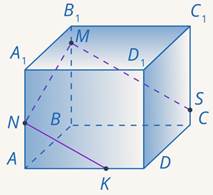
Рис. 38. Иллюстрация к задаче 10

Через 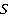  в плоскости правой грани проводим прямую, параллельную  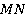, получаем точку  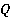. Сечение построено (см. рис. 39).

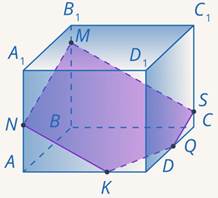
Рис. 39. Иллюстрация к задаче 10

Задача 11. Построить сечение тетраэдра по трем точкам (см. рис. 40).

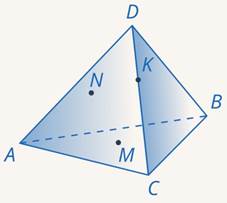
Рис. 40. Иллюстрация к задаче 11

Решение

Точки, задающие плоскость сечения, конечно, не обязаны находиться на ребрах многогранника. Рассмотрим тетраэдр. Точка 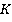  лежит на ребре  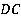. А вот, где лежит точка  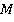, по рисунку мы понять не можем. Это может быть и нижняя грань, и левая. В таких случаях нужно явно проговаривать, где лежит точка.

Пусть точка 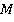  лежит на нижней грани, а точка  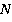 – на левой. Точк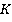и   и 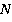  лежат на одной грани – левой. Проводим через них прямую до пересечения с  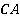, которая тоже лежит в левой грани. Получили точку сечения  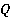 и точку  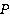, лежащую в плоскости нижней грани (см. рис. 41).

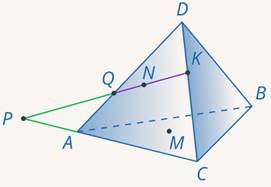
Рис. 41. Иллюстрация к задаче 11

Проводим прямую 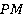 . Получили еще две точки сечения  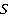 и 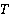  (см. рис. 42).

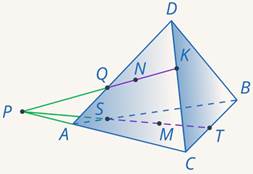
Рис. 42. Иллюстрация к задаче 11

Соединяем все точки сечения, лежащие на одних гранях. Многоугольник замкнулся, сечение построено (см. рис. 43).