Задачи на сплавы и смеси

• Решение задач на смеси и сплавы.

• Цель:

Подготовка учащихся к государственной итоговой аттестации.

Рассмотреть различные способы решения задач.

Отрабатывать практические навыки решения задач по изученной теме.

Задача №1

В двух сплавах меди и цинка отношение меди к цинку 4:3 и 2:3 соответственно. После совместной переплавки 140 кг первого сплава, 150 кг второго и некоторой массы чистой меди получили сплав, в котором меди на 20 кг больше, чем цинка. Найти массу нового сплава.

Решение:

3/7 * 140 + 3/5 * 150 = 150 (кг) цинка содержал полученный сплав.

150 + 20 = 170 (кг) меди содержал полученный сплав (на 20 кг больше).

150 + 170 = 320 (кг) масса полученного сплава.

Ответ: 320 кг масса полученного сплава.

Задача № 2 .

В сосуд содержащий 2 кг 80 % -го водного раствора уксуса добавили 3 кг воды. Найдите концентрацию получившегося раствора уксусной кислоты.

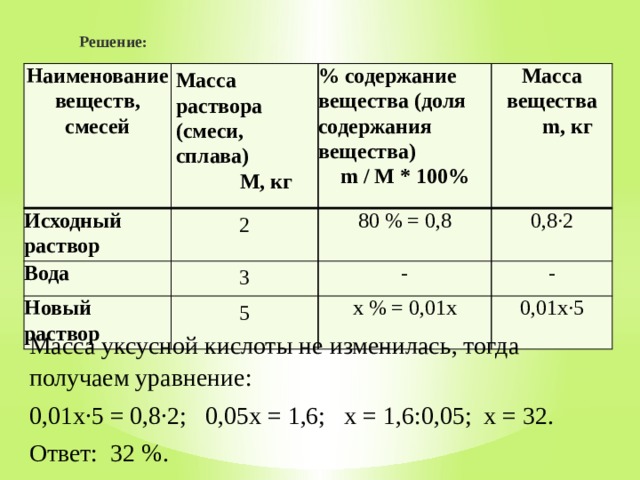
Решение:

Наименование веществ, смесей

Масса раствора (смеси, сплава)

Исходный раствор

М, кг

% содержание вещества (доля содержания вещества)

2

Вода

Новый раствор

m / M * 100%

Масса вещества

80 % = 0,8

3

5

0,8·2

-

m, кг

-

х % = 0,01х

0,01х·5

Масса уксусной кислоты не изменилась, тогда получаем уравнение:

0,01х·5 = 0,8·2; 0,05х = 1,6; х = 1,6:0,05; х = 32.

Ответ: 32 %.

Задача № 3 .

Смешали некоторое количество 12% раствора соляной кислоты с таким же количеством 20 % раствора этой же кислоты. Найти концентрацию получившейся соляной кислоты.

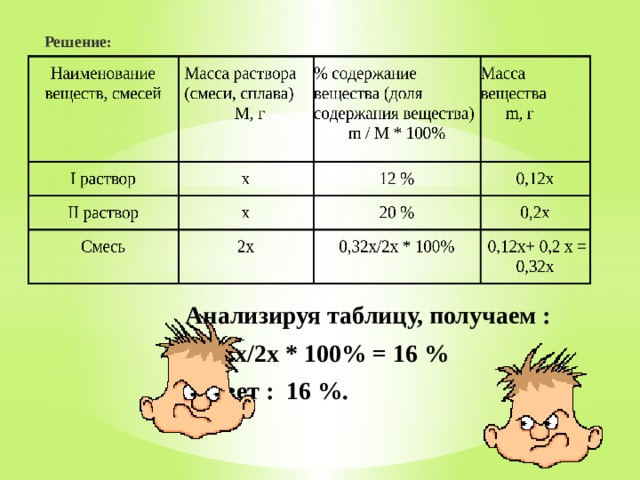
Решение:

Анализируя таблицу, получаем :

0,32х/2х * 100% = 16 %

Ответ : 16 %.

Задача № 4.

Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?

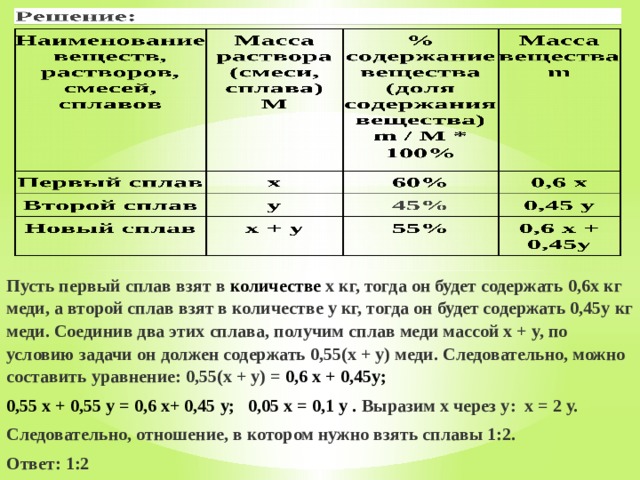
Пусть первый сплав взят в количестве x кг, тогда он будет содержать 0,6x кг меди, а второй сплав взят в количестве y кг, тогда он будет содержать 0,45y кг меди. Соединив два этих сплава, получим сплав меди массой x + y, по условию задачи он должен содержать 0,55(x + y) меди. Следовательно, можно составить уравнение: 0,55(x + y) = 0,6 х + 0,45у;

0,55 х + 0,55 у = 0,6 х+ 0,45 у; 0,05 х = 0,1 у . Выразим x через y: х = 2 у.

Следовательно, отношение, в котором нужно взять сплавы 1:2.

Ответ: 1:2

Задача №5.

Име­ют­ся два со­су­да, со­дер­жа­щие 4 кг и 16 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 57% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 60% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

Ре­ше­ние:

Задача № 6.  

Сме­шав 60% и 30% рас­тво­ры кис­ло­ты и, до­ба­вив 5 кг чи­стой воды, по­лу­чи­ли 20% рас­твор кис­ло­ты. Если бы вме­сто 5 кг воды до­ба­ви­ли 5 кг 90% рас­тво­ра той же кис­ло­ты, то по­лу­чи­ли бы 70% рас­твор кис­ло­ты. Сколь­ко ки­ло­грам­мов 60% рас­тво­ра ис­поль­зо­ва­ли для по­лу­че­ния смеси?

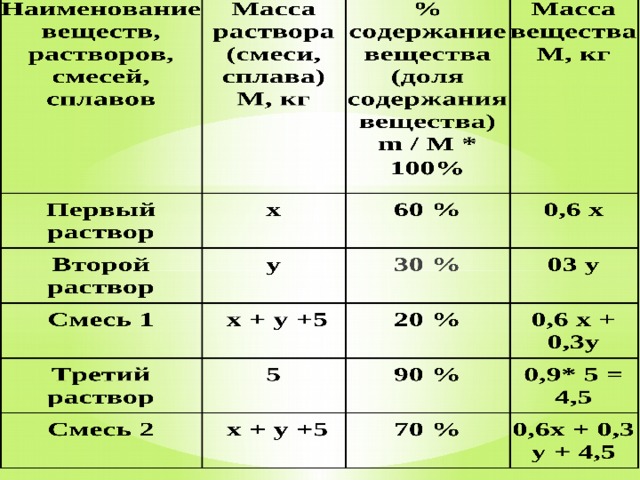
Задача № 7

Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?

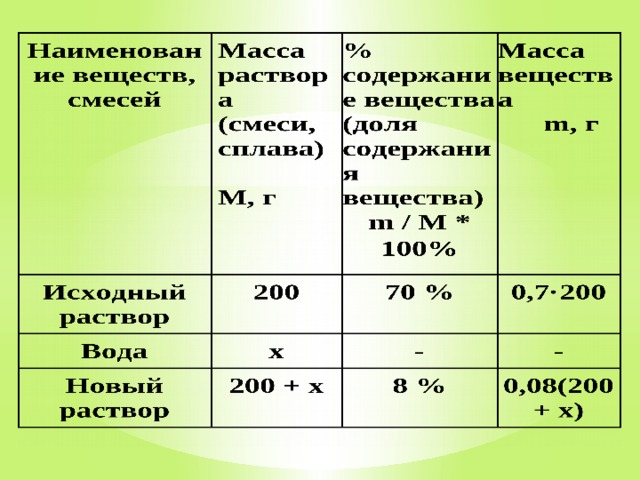
Анализируя таблицу, составляем уравнение :

0,08(200 + х) = 0,7·200; 16 + 0,08х = 140; 0,08х = 124; х = 1550.

Ответ :1,55 кг воды.