Задачи на тему "Импульс тела. Импульс силы. Закон сохранения импульса"

Импульс тела. Импульс силы. Закон сохранения импульса

1. Тело массой m = 100 г падает свободно. Определите изменение импульса этого тела за первые две секунды падения.

Решение

Тело массой m = 100 г падает свободно. Определите изменение импульса этого тела за первые две секунды падения.

Свободно падая тело через 2 с приобретет скорость

.

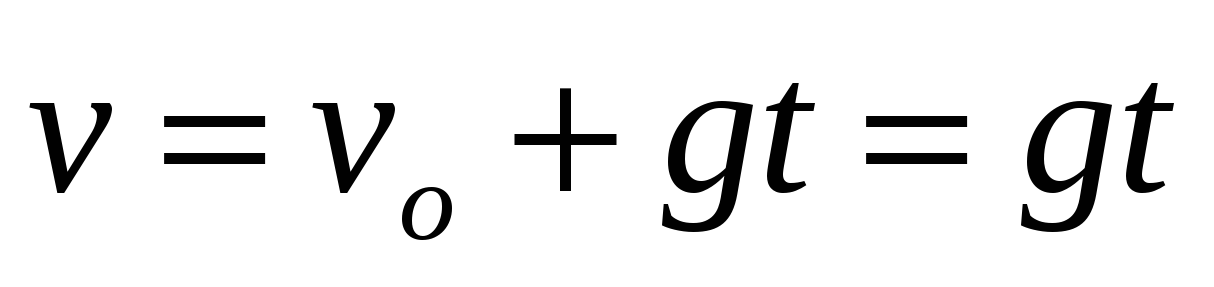Изменение импульса равно

.

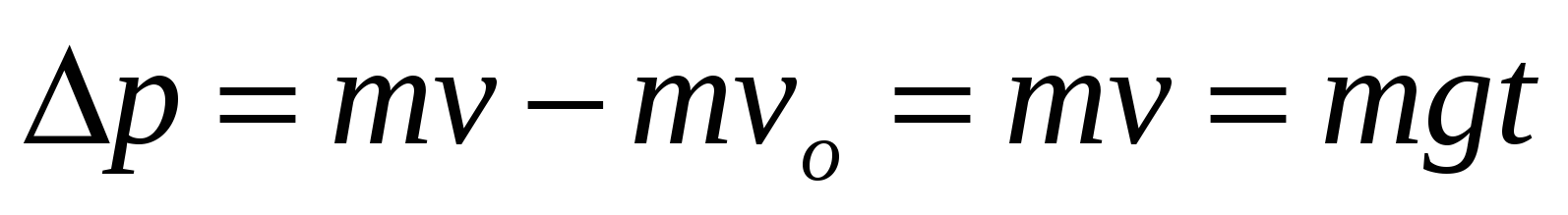После вычислений

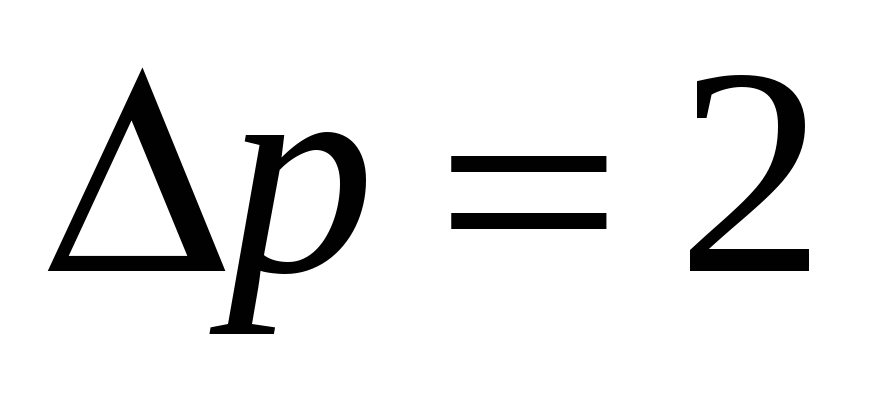Нс.

1. Плот массой m₁ свободно скользит по поверхности воды со скоростью v₁. На плот с берега прыгает человек массы m₂. Скорость человека перпендикулярна к скорости плота и равнаv₂. Определить скорость v плота с человеком. Силами трения плота о воду пренебречь

Решение

Так как внешних сил в момент прыжка нет, выполняется закон сохранения импульса.

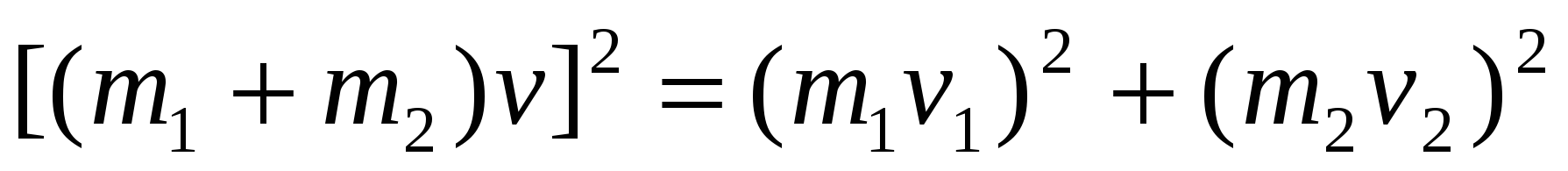
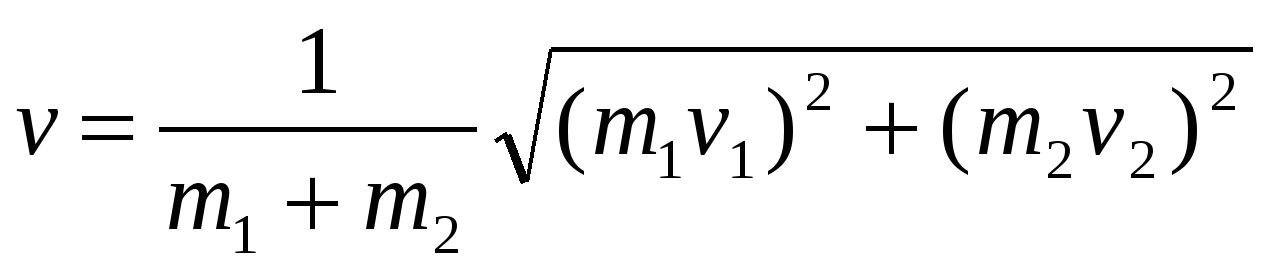
Эта скорость образует с первоначальным направлением движения плота угол , причем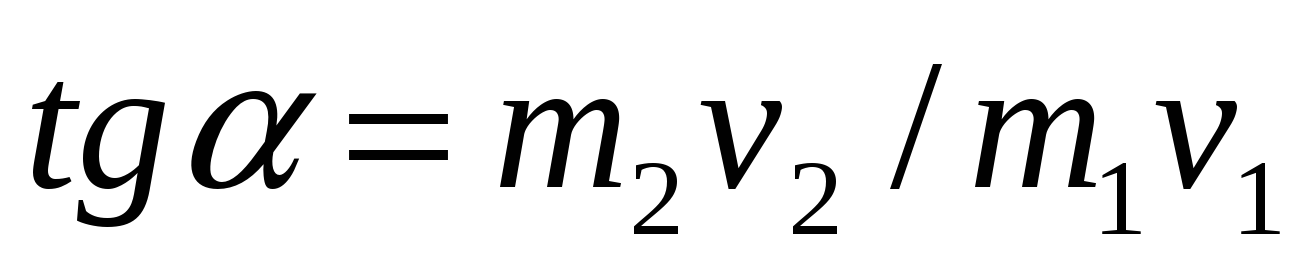

1. Вертикально вверх произведен выстрел из пушки. Начальная скорость снаряда v_o. В точке максимального подъема снаряд разорвался на две равные по массе половины. Первая упала вблизи точки выстрела, имея скорость 2v_o. Через какое время после выстрела упадет вторая половина? Какую скорость она будет иметь в момент падения? 

Решение

В момент взрыва полный импульс равен нулю (максимальная точка подъема).

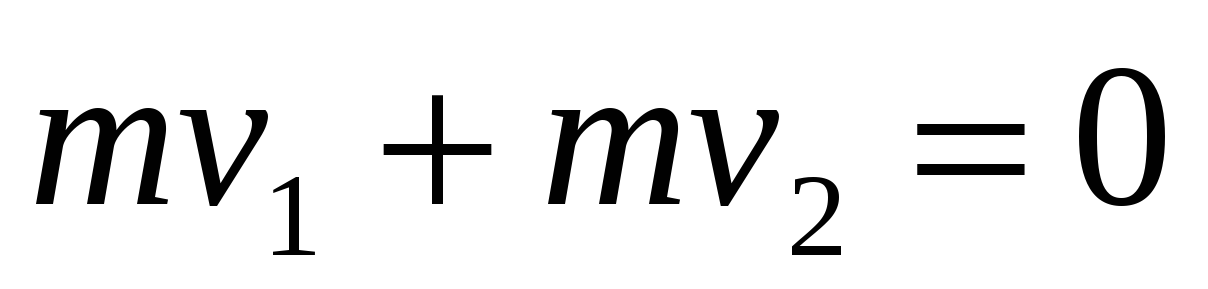или .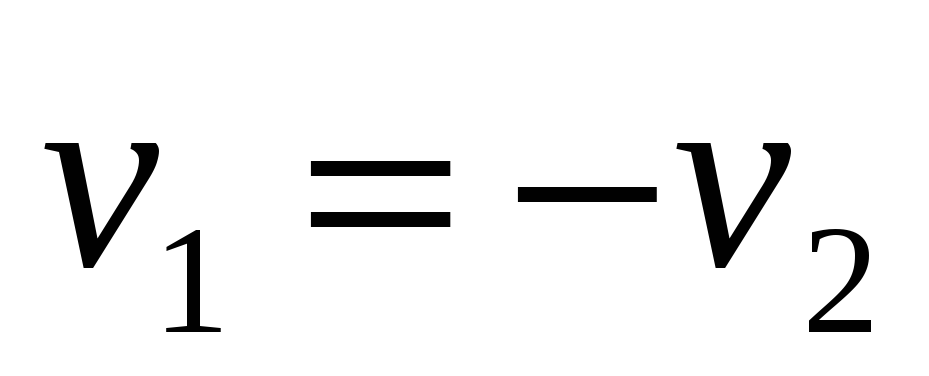

Высота, на которой разорвался снаряд, равна 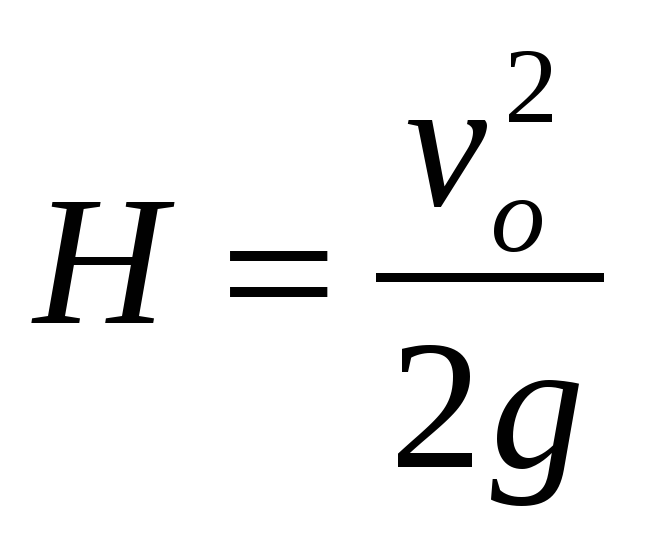. Из закона сохранения энергии для первого осколка получим

,

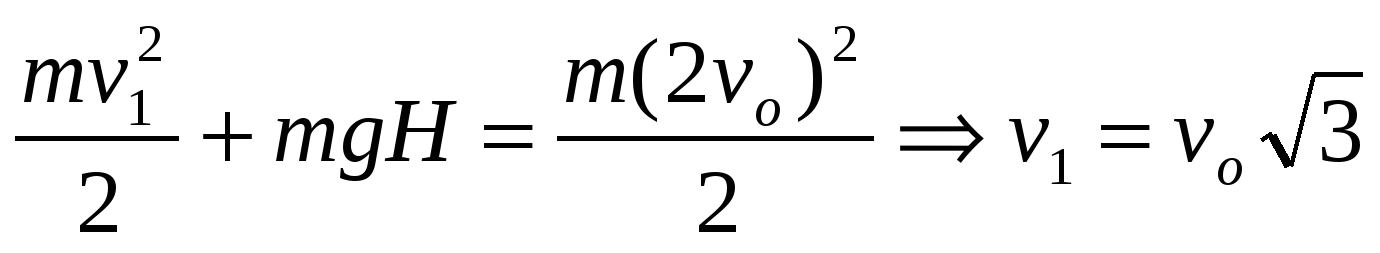следовательно, .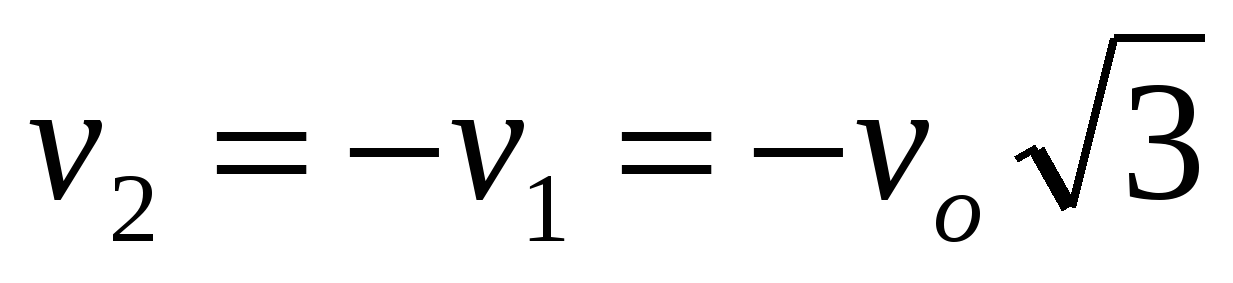

На землю второй осколок упадет с той же скоростью, что и первый осколок. Время его падения t складывается из времени подъема t₁ на максимальную высоту и времени падения t₂ с этой высоты вниз.

, .

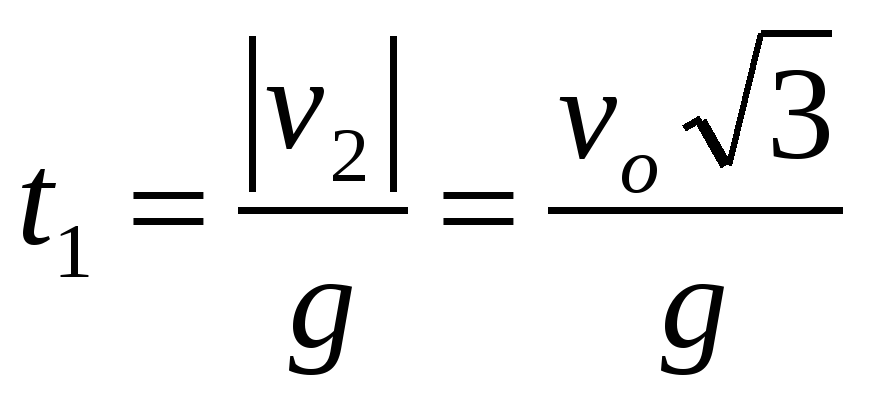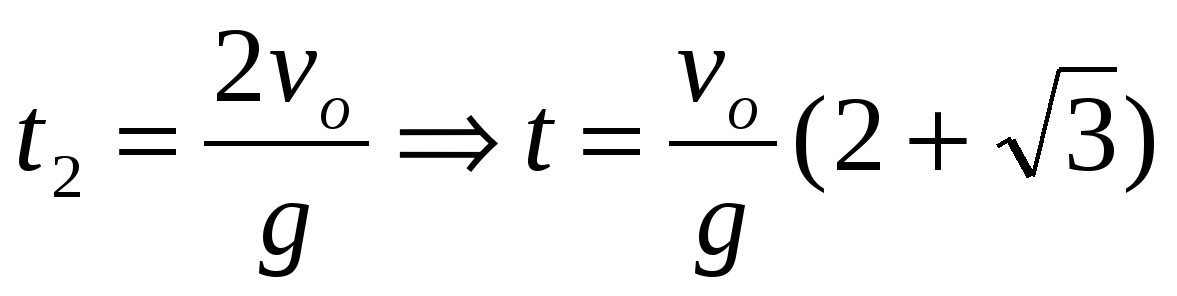1. Математический маятник, т. е. небольшой шарик на тонкой нити, массой которого можно пренебречь, первоначально находится в горизонтальном положении. Длина нити маятника l. На расстоянии l/2 под точкой подвеса расположена горизонтальная плита. На какую высоту поднимется шарик после удара о плиту. Удар упругий. 

Решение

При ударе маятника о плиту горизонтальная составляющая скорости не изменится, а вертикальная, сохранив свою величину, изменит направление на противоположное. Так как

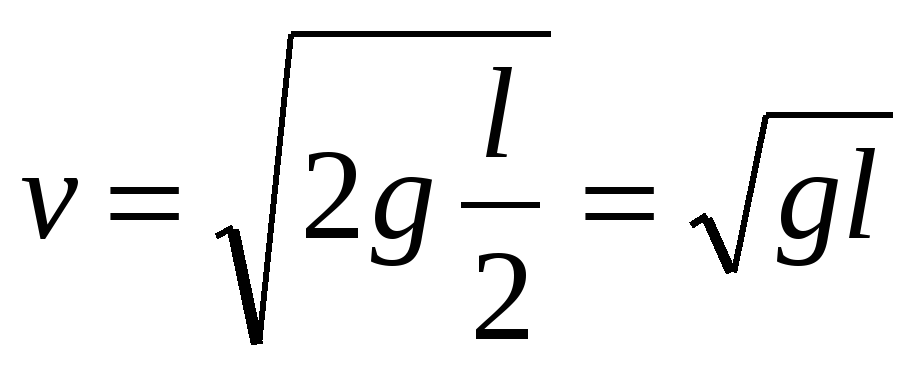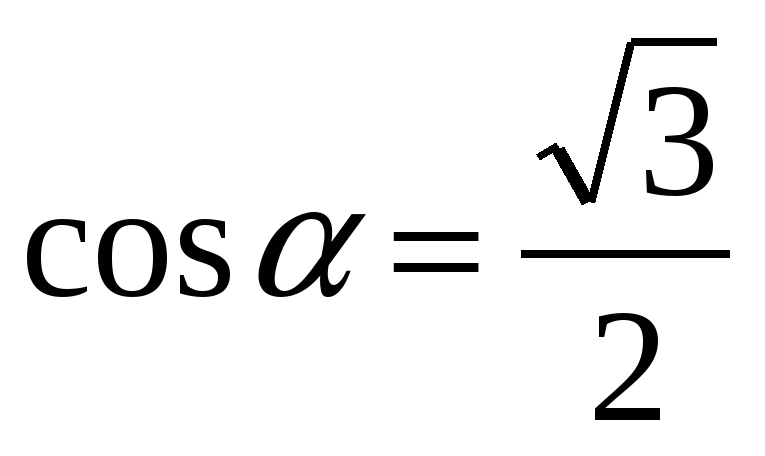и , то .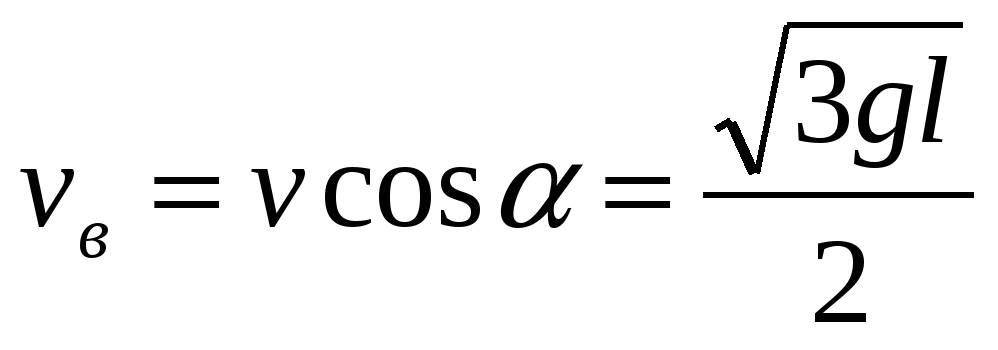

Высота h, на которую поднимется маятник, равна

.

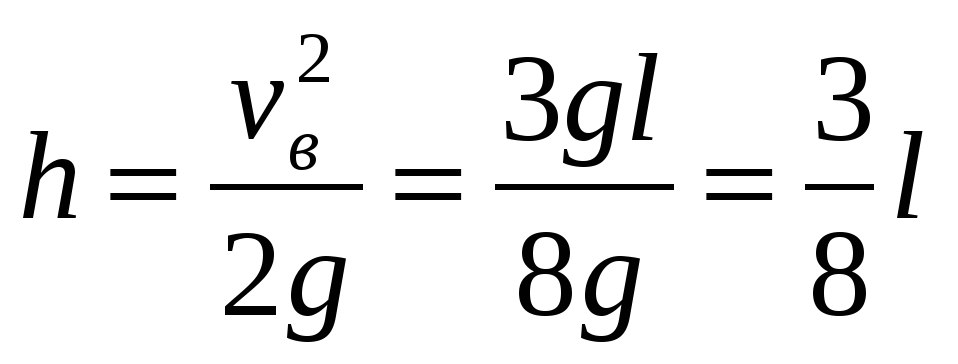1. Призма с массой M и с углом наклона  стоит на гладкой горизонтальной поверхности льда. На призме стоит собака, масса которой m. С какой скоростью будет двигаться призма, если собака побежит вверх со скоростью v относительно призмы? Трением пренебречь.

Решение

В задаче сохраняется составляющая количества движения по горизонтали, так как в этом направлении внешние силы не действуют. Пусть v₁ скорость призмы. Горизонтальная составляющая скорости собаки относительно льда будет 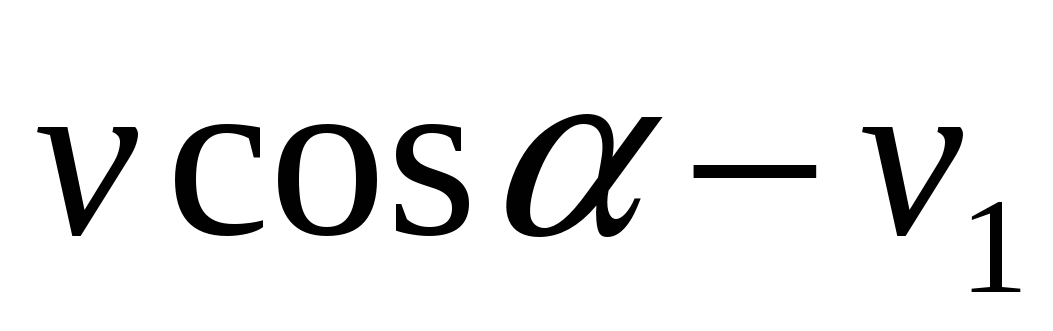, тогда

.

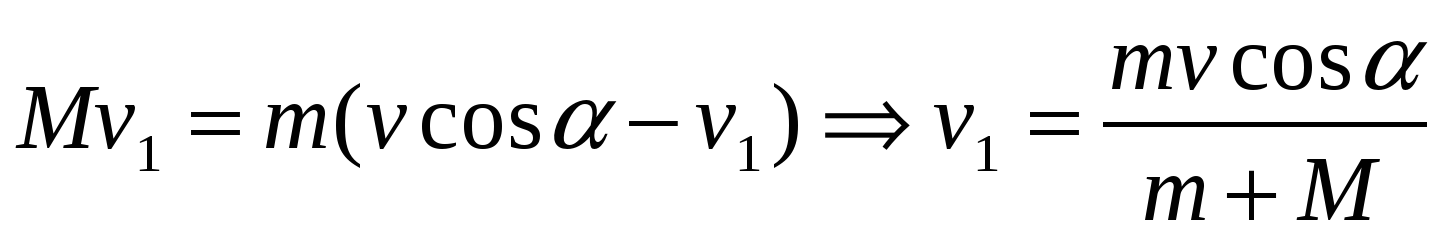1. Легкий теннисный мячик ударили ногой, и он полетел в направлении движения ноги. Какую скорость приобрел мячик, если скорость движения ноги при ударе u = 10 м/с.

Решение

Соударение ноги с мячиком можно считать упругим и центральным. Масса ноги во много раз превышает массу мячика, поэтому скорость ноги при ударе практически не изменяется. Удобно рассмотреть столкновение в системе отсчета, связанной с массивным телом (ногой). В этой системе отсчета начальная скорость мячика по модулю равна u, и при упругом ударе эта скорость изменяет направление на противоположное, не изменяясь по величине. Следовательно, скорость мячика относительно Земли м/с.

1. Через блок, перекинут шнур, на концах которого закреплены грузы массой M. На высоте h находится кольцо, которое скользит без трения. Через какое время t расстояние между грузами станет h, после свободного падения кольца. 

Решение

Кольцо, падая с высоты h неупруго, взаимодействует с грузом M, сообщая ему начальную скорость, которую можно определить, применив закон сохранения импульса

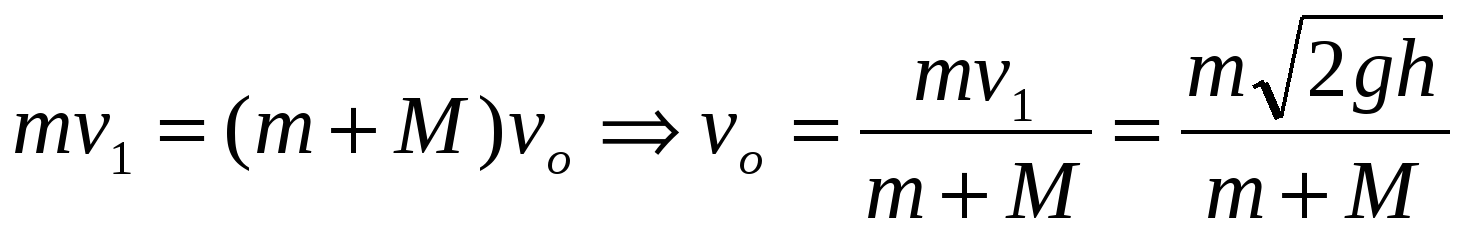(1).

После взаимодействия, грузы будут двигаться с равным ускорением

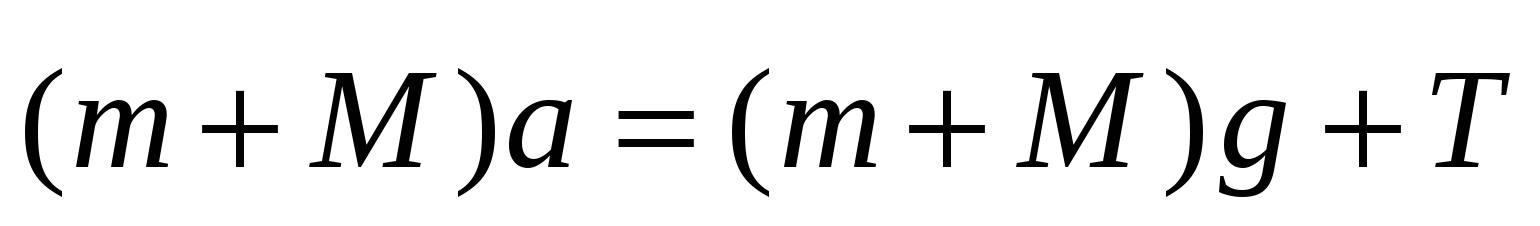и .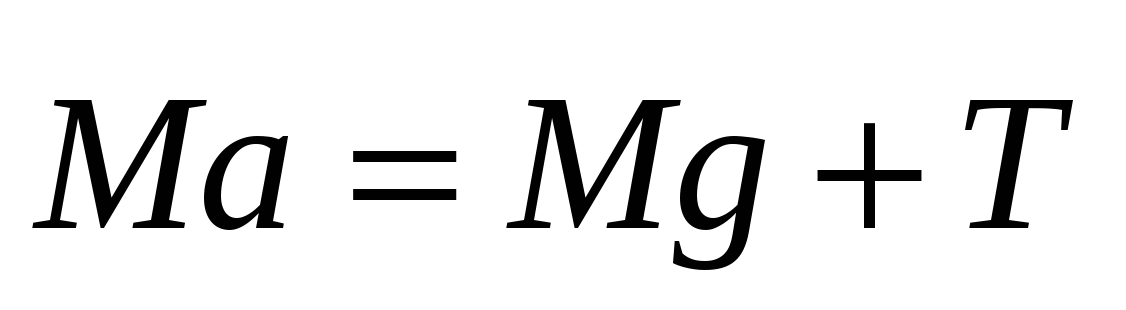

Проецируя оба уравнения на выбранное направление и решая совместно, находим

(2).

Расстояние (3), грузы проходят за искомое время t. Подставляя замену в уравнение (3) вместо начальной скорости (1) и ускорения (2), получим уравнение:

.

Решая это уравнение, находим время

.

Отрицательное значение времени по смыслу задачи не подходит, следовательно

.

1. Человек, имеющий массу M, прыгает под углом  к горизонту со скоростью v_o. В верхней точке траектории он бросает со скоростью v₁ вертикально вниз груз массой m. На какую общую высоту H подпрыгнул человек? 

Решение

Найдем высоту h верхней точки траектории полета человека

.

В верхней точке происходит неупругое взаимодействие без участия внешних сил. Поэтому импульс человека компенсируется импульсом груза: . Откуда скорость вертикального подъема человека . Далее по оси Y человек поднимается, как тело, брошенное вертикально вверх, т. е. . Общая высота подъема

.

1. Массивная плита движется с постоянной скоростью u_o в положительном направлении оси X, выбранной неподвижной системы отсчета (ось X перпендикулярна к плите). Шарик массы m движется со скоростью v_o в направлении, указанном на рисунке. Определить величину и направление скорости шарика v после удара о плиту, если удар абсолютно упругий

Решение

При абсолютно упругом ударе составляющая скорости шарика, параллельная плите, не изменяется. Поэтому . В системе отсчета, связанной с плитой, составляющая скорости шарика, перпендикулярная к плите, изменит направление на противоположное. Обозначим через и векторы скорости шарика относительно плиты до и после удара соответственно. Тогда, используя закон сложения скоростей, получим

Из полученных соотношений определим величину скорости шарика после удара v и угол  между вектором скорости и осью x:

, .

.

, , ,

1. Ядро, летевшее в горизонтальном направлении со скоростью 20 м/с, разорвалось на два осколка массами 10 кг и 5 кг. Скорость меньшего осколка равна 90 м/с и направлена вертикально вверх. Определить модуль и направление скорости большего осколка

Решение

Система «ядро – осколки» не замкнута вследствие действия силы тяжести. Однако задача может быть решена на основании закона сохранения импульса, так как время разрыва мало. Изобразим на чертеже векторы импульсов тел системы непосредственно перед и после разрыва. Запишем закон сохранения импульса в векторной форме:

.

Ось X направим горизонтально, ось Y – вертикально, угол между вектором и осью X обозначим . Проецируем векторные величины на ось X и Y:

. ; .

После вычислений, находим м/с,  = 29^о.