ЕГЭ. Задание № 17
I. Банки, вклады, кредиты
Замечание 1. Если первоначальная сумма вклада x руб., а процент годовых p %, то сумма вклада через один год составит  руб.
руб.
Замечание 2. Если первоначальная сумма вклада x руб., а процент годовых p %, то сумма вклада через n лет составит  руб.
руб.
Задача. Спустя два года после того, как некоторая сумма внесена в банк, вклад за счет процентов увеличился на 2200 руб. Если бы первоначальная сумма была на 1000 руб. больше, то итоговая прибыль равнялась бы 2640 руб. Чему равен процент годовых, если он за два года не менялся?
Решение. Рассмотрим изменение вклада за два года.
|
| Сумма за счёт процентов (руб.) | Сумма (руб.) | % годовых |
| Первоначально |
| x |
|
| Через 2 год |  | x + 2200 | y |
| Первоначально |
| x + 1000 |
|
| Через 2 год |  | x + 1000 + 2640 | y |
x, y 0.
Составим систему уравнений
 Ответ: 20 %.
Ответ: 20 %.
1. В банк положен вклад из расчета 20 % годовых. Через какое наименьшее количество лет вклад увеличится в 2 раза? Ответ: 4 года
2. Клиент положил некоторую сумму в банк. При одинаковом проценте годовых через три года была получена сумма в 1,728 раз превышающая первоначальную. Какой процент годовых выплачивал банк? Ответ: 20 %
3. Себестоимость продукции сначала повысилась на 10%, а затем понизилась на 20%. На сколько процентов понизилась себестоимость продукции? Ответ: на 12 %
4. Фермер получил кредит в банке под определенный процент годовых. Через год фермер в счет погашения кредита вернул в банк 75 % от всей суммы, которую он должен банку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму на 21% превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке? Ответ: 120 %
5. Если 1 кубометр газа на 50 % дороже 1 кг угля и дает тепла на 20 % больше, то на сколько процентов при переходе с угля на газ возрастут расходы на топливо при прочих равных условиях? Ответ: 25 %
6. 31 декабря Сергей взял в банке 9 930 000 рублей в кредит под 10 % годовых. Схема выплаты кредита следующая: 31 декабря каждого года банк начисляет проценты на оставшуюся сумму долга (от есть увеличивает долг на 10 %), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
7. 1 июня 2013 года Всеволод Ярославович взял в банке 900 000 рублей в кредит. Схема выплаты кредита следующая – 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1 %), затем Всеволод Ярославович переводит в банк платёж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные выплаты были не более 300 000 рублей?


9. 15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в процентах от кредита) | 100% | 90% | 80% | 70% | 60% | 50% | 0% |
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5 %, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
10. В начале года  некоторой суммы денег вложили в банк А, а то, что осталось – в банк Б. Если вклад находится в банке с начала года, то к концу года он возрастает на определённый процент, величина которого зависит от банка. Известно, что к концу первого года сумма вкладов стала равна 670 у.е., к концу следующего – 749 у.е. Если первоначально
некоторой суммы денег вложили в банк А, а то, что осталось – в банк Б. Если вклад находится в банке с начала года, то к концу года он возрастает на определённый процент, величина которого зависит от банка. Известно, что к концу первого года сумма вкладов стала равна 670 у.е., к концу следующего – 749 у.е. Если первоначально  суммы было бы вложено в банк Б, а оставшуюся вложили бы в банк А, то по истечении одного года сумма выросла бы до 710 у.е. Определите сумму вкладов по истечении второго года в этом случае.
суммы было бы вложено в банк Б, а оставшуюся вложили бы в банк А, то по истечении одного года сумма выросла бы до 710 у.е. Определите сумму вкладов по истечении второго года в этом случае.
Ответ: 841
11. Фермер получил кредит в банке под определённый процент годовых. Через год фермер в счёт погашения кредита вернул в банк  от всей суммы, которую он был должен банку к этому времени, а ещё через год в счёт полного погашения кредита он внёс в банк сумму, на 21 % превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?
от всей суммы, которую он был должен банку к этому времени, а ещё через год в счёт полного погашения кредита он внёс в банк сумму, на 21 % превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?
Ответ: 120
12. Спустя два года после того, как некоторая сумма внесена в банк, вклад за счет процентов увеличился на 4400 руб. Если бы первоначальная сумма была на 2000 руб. больше, то итоговый доход равнялся бы 5280 руб. Чему равен процент годовых, если он за два года не менялся? Под доходом понимается разница между итоговой суммой и первоначальной. Процент годовых – это процент, на который увеличивается сумма вклада за один год.
Решение. 1. Обозначим через x руб. первоначальную сумму вклада, а через k – коэффициент на который будет умножаться сумма вклада каждый год.
2. Получим систему уравнений

3. Разделив второе уравнение системы на первое, получим линейное уравнение, корнем которого является x = 10 000 руб.
4.  ; k = 1,44; k = 1,2. Процент годовых равен 20%.
; k = 1,44; k = 1,2. Процент годовых равен 20%.
Ответ: 20%.
13. По прогнозу экспертов, цены на квартиры в Москве через год упадут: в рублях на 20%, в евро на 40%. А в Сочи цены в рублях упадут на 10%. На сколько процентов упадут цены на квартиры в Сочи в евро?
Ответ: 32,5 %
14. При рытье колодца глубиной свыше 10 м за первый метр заплатили 1000 руб., а за каждый следующий на 500 руб. больше, чем за предыдущий. Сверх того за весь колодец дополнительно было уплачено 10000 руб. Средняя стоимость 1 м оказалась равной 6250 руб. Определите глубину колодца.
Ответ: 20.
15. Молодой семье на покупку квартиры банк выдает кредит под 20 % годовых. Схема выплаты кредита следующая: ровно через год после выдачи кредита банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20 %), затем эта семья в течение следующего года переводит в банк определенную (фиксированную) сумму ежегодного платежа. Семья Ивановых планирует погашать кредит равными платежами в течение 4 лет. Какую сумму может предоставить им банк, если ежегодно Ивановы имеют возможность выплачивать по кредиту 810 000 рублей?
Ответ: 2 096 875
16. Банк планирует вложить на 1 год 30% имеющихся у него средств клиентов в акции золотодобывающего комбината, а остальные 70% – в строительство торгового комплекса. В зависимости от обстоятельств первый проект может принести банку прибыль в размере от 32% до 37% годовых, а второй проект – от 22% до 27% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке, уровень которой должен находиться в пределах от 10% до 20% годовых. Определите, какую наименьшую и наибольшую чистую прибыль в процентах годовых от суммарных вложений в покупку акций и строительство торгового комплекса может при этом получить банк.
Ответ: 5% и 20%.
17. 31 декабря 2010 года Дмитрий взял в банке 5 005 000 рублей в кредит под 20 % годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20 %), затем Дмитрий переводит в банк платёж. Весь долг Дмитрий выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы выплатил долг за 2 равных платежа?
18. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем 12%, потом  % и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на
% и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на  %. Определите срок хранения вклада.
%. Определите срок хранения вклада.
Ответ: 7
19. (ЕГЭ-2015) 15-го января планируется взять кредит в банке на 14 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 15% больше суммы, взятой в кредит. Найдите r.
20. (ЕГЭ-2015) В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн рублей? Ответ: 4.
21. (ЕГЭ-2017) В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплачивать одним платежом часть долга Сколько рублей было взято в банке, если известно, что кредит был полностью погашен тремя равными платежами (то есть за 3 года) и сумма платежей превосходит взятую в банке сумму на 77200 рублей?
22. (ЕГЭ-2018) 15-го декабря планируется взять кредит в банке на 26 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца с 1-го по 25-й долг должен быть на 20 тысяч рублей меньше долга на 15-е число предыдущего месяца;
– к 15-му числу 26-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 25-го месяца, если общая сумма выплат после полного погашения кредита составит 1407 тысяч рублей?
Решение. Пусть 15-го числа 25-го месяца долг составит B тысяч рублей. По условию, долг перед банком (в тыс. рублей) по состоянию на 15-е число должен уменьшаться до нуля следующим образом:
B + 500; B + 480; B + 460; ...; B + 20; B; 0.
Первого числа каждого месяца долг возрастает на 3%, значит, последовательность размеров долга (в тыс. рублей) по состоянию на 1-е число такова:
1,03(B + 500); 1,03(B + 480); ...; 1,03(B + 20); 1,03 ∙ B.
Следовательно, выплаты (в тыс. рублей) должны быть следующими:
0,03(B + 500) + 20; 0,03(B + 480) + 20; ...; 0,03(B + 20) + 20; 1,03 ∙ B.
Всего следует выплатить

II. Задачи на оптимальный выбор
1. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у. е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у. е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?
Ответ: 5 рабочих на 1-й объект, 19 рабочих на 2-й объект; 461 у.е.
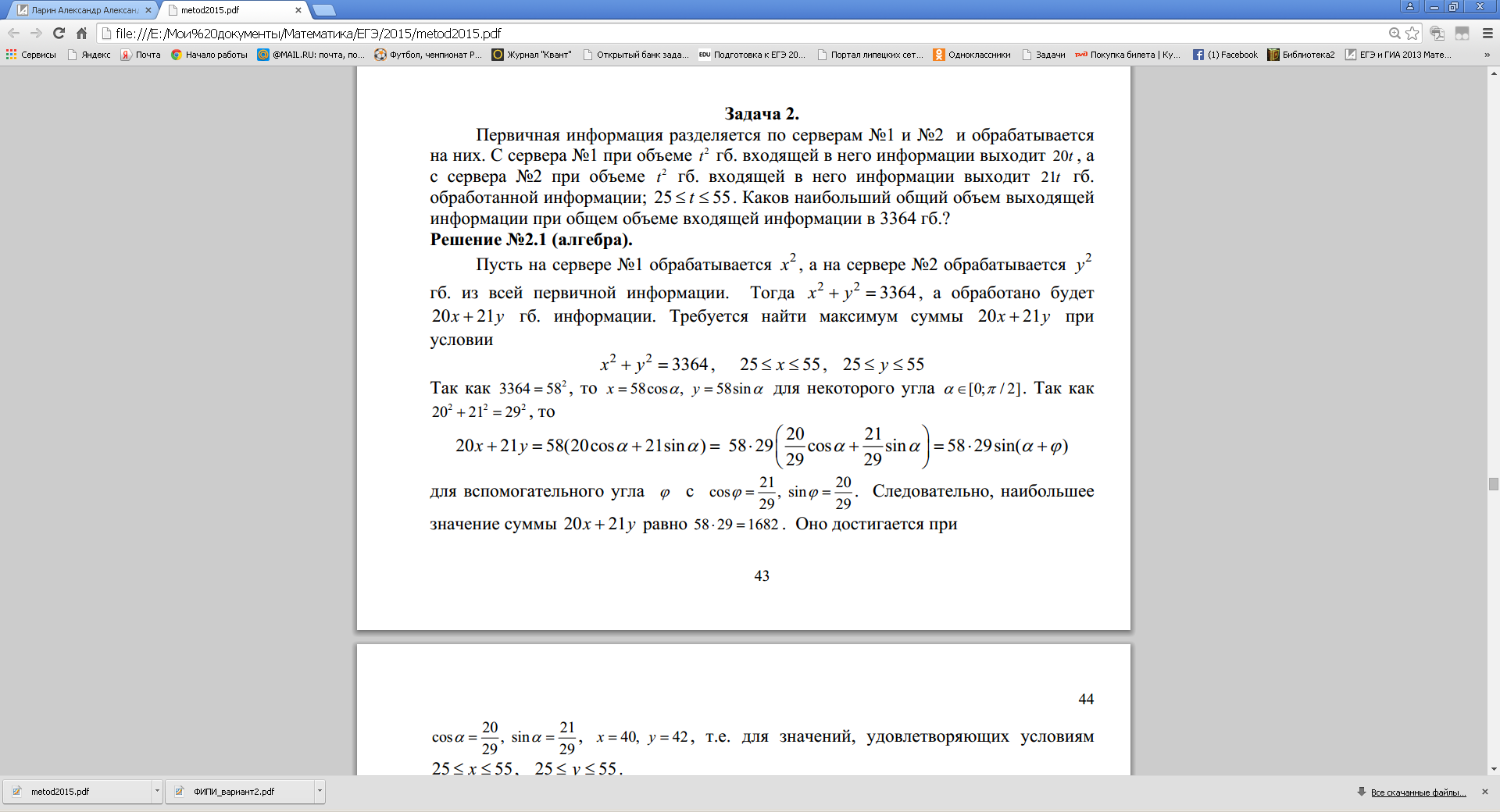
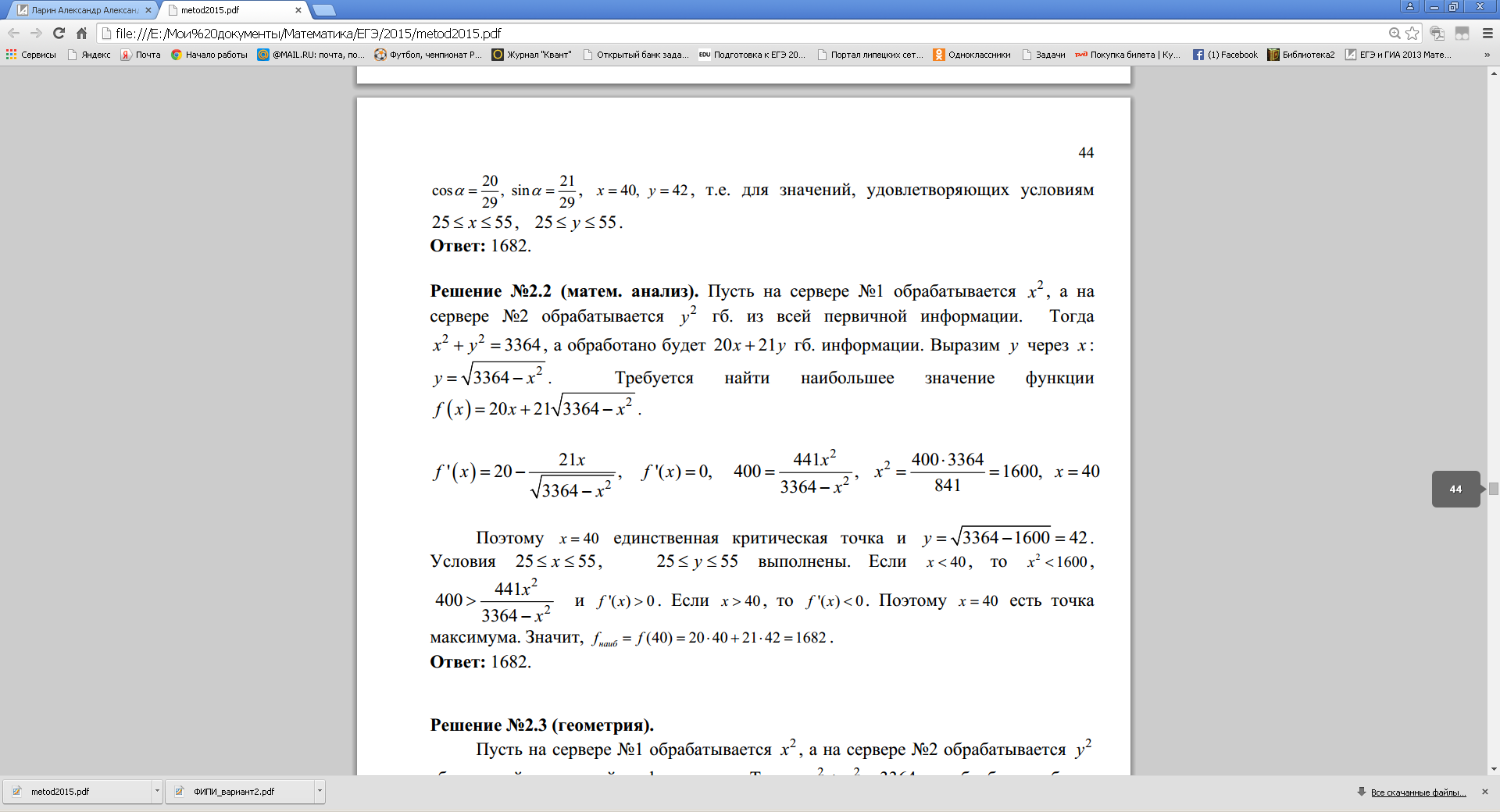
2. Первичная информация разделяется по серверам № 1 и № 2 и обрабатывается на них. С сервера № 1 при объеме t2 гб. входящей в него информации выходит 20t, а с сервера № 2 при объеме
t2 гб. входящей в него информации выходит 21t гб. обработанной информации; 25 t 3 364 гб.?

3. ЕГЭ-2017. Пенсионный фонд владеет ценными бумагами, которые стоят 10t тыс. рублей в конце года t (t = 1; 2; 3; ...). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счет в банке, при этом в конце каждого следующего года сумма на счете будет увеличиваться в 1 + r раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счете была наибольшей. Расчеты показали, что для этого ценные бумаги нужно продавать строго в конце одиннадцатого года. При каких положительных значениях r это возможно?
Ответ: 1/11 r
4. (ФИПИ, ЕГЭ-2016). В двух шахтах добывают алюминий и никель. В первой шахте работают 20 шахтеров, каждый из которых трудится 5 часов в день. При этом один шахтер за час добывает 1 кг алюминия или 2 кг никеля. Во второй шахте работают 100 шахтеров, каждый из которых трудится 5 часов в день. При этом один шахтер за час добывает 2 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение. Пусть в первой шахте х чел ∙ час, а во второй шахте у чел ∙ час потрачены на добычу алюминия. Составим таблицу по данным задачи.
|
| Алюминий | Никель |
|
| Чел ∙ час | Количество | Чел ∙ час Количество | Количество |
|
|
| металла, кг |
| металла, кг |
| Шахта 1 | х | х | 100 - х | 2(100 - х) |
| Шахта 2 | у | 2у | 500 – y | 500 - у |
| Всего |
| х +2 у |
| 700 -2х - у |
Ответ: 1050 кг.
5. (ЕГЭ-2015). Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решение. Пусть на первом заводе работают суммарно х2, а на втором – у2 часов в неделю. Требуется найти максимум суммы S = 3х + 4у при условии
500(х2 + у2) = 5 000 000; х2 + у2 = 10 000; x, y [0; 100]. (*)
1 способ. Выразим  и максимизируем функцию
и максимизируем функцию  , при условии x [0; 100].
, при условии x [0; 100].
2 способ. Выразим из первого соотношения у = 4(S – 3х), подставим в (*), получим уравнение
x2 + 16 ∙ (S – 3x)2 = 10 000.
Ответ: 500.
6. (ФИПИ, ЕГЭ-2016). В двух областях работают по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,3 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко-часов труда, а для добычи у кг никеля в день требуется у2 человеко-часов труда.
Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно добыть в двух областях суммарно для нужд промышленности?
Ответ: 280 кг.
7. (ЕГЭ-2015) Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 2t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 5t единиц товара.
За каждый час работы (на каждом из заводов) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 580 единиц товара. Какую наименьшую сумму придется тратить еженедельно на оплату труда рабочих?
8. Строительство нового завода стоит 78 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 0,5х2 + 2x + 6 млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит
px – (0,5x2 + 2x + 6). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более, чем за 3 года? Ответ: 10







 руб.
руб. руб.
руб.

 Ответ: 20 %.
Ответ: 20 %.



 некоторой суммы денег вложили в банк А, а то, что осталось – в банк Б. Если вклад находится в банке с начала года, то к концу года он возрастает на определённый процент, величина которого зависит от банка. Известно, что к концу первого года сумма вкладов стала равна 670 у.е., к концу следующего – 749 у.е. Если первоначально
некоторой суммы денег вложили в банк А, а то, что осталось – в банк Б. Если вклад находится в банке с начала года, то к концу года он возрастает на определённый процент, величина которого зависит от банка. Известно, что к концу первого года сумма вкладов стала равна 670 у.е., к концу следующего – 749 у.е. Если первоначально  от всей суммы, которую он был должен банку к этому времени, а ещё через год в счёт полного погашения кредита он внёс в банк сумму, на 21 % превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?
от всей суммы, которую он был должен банку к этому времени, а ещё через год в счёт полного погашения кредита он внёс в банк сумму, на 21 % превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?
 ; k = 1,44; k = 1,2. Процент годовых равен 20%.
; k = 1,44; k = 1,2. Процент годовых равен 20%.
 % и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на
% и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на  %. Определите срок хранения вклада.
%. Определите срок хранения вклада.


 и максимизируем функцию
и максимизируем функцию  , при условии x [0; 100].
, при условии x [0; 100].









