Задача 1
Даны четыре действительных числа: x1, y1, x2, y2.
Напишите функцию distance(x1, y1, x2, y2), вычисляющую расстояние между точкой (x1,y1) и (x2,y2). Считайте четыре действительных числа и выведите результат работы этой функции.
Входные данные
Вводятся четыре действительных числа.
Выходные данные
Выведите ответ на задачу.
Примеры
Входные данные
0
0
1
1
Выходные данные
1.41421
Задача 2
Числа Фибоначчи — это последовательность чисел, которые задаются по определённому правилу. Оно звучит так: каждое следующее число равно сумме двух предыдущих. Первые два числа заданы сразу и равны 0 и 1.
Пример: 0 1 1 2 3 5 8 и т.д.
Напишите функцию phib(n), которая по данному целому неотрицательному n возвращает n-e число Фибоначчи. В этой задаче нельзя использовать циклы - используйте рекурсию.
phib(1) = phib(2) = 1.
phib(n) = phib(n - 1) + phib(n - 2)
Входные данные
Вводится целое число.
Выходные данные
Выведите ответ на задачу.
Примеры
Входные данные
6
Выходные данные
8
Задача 3
Сочетанием из n элементов по k называется подмножество этих n элементов размера k.
Два сочетания называются различными, если одно из сочетаний содержит элемент, который не содержит другое.
Числом сочетаний из n по k называется количество различных сочетаний из n по k. Обозначим это число за C(n, k).
Пример:
Пусть n = 3, т. е. есть три элемента (1, 2, 3). Пусть k = 2.
Все различные сочетания из 3 элементов по 2: (1, 2), (1, 3), (2, 3).
Различных сочетаний три, поэтому C(3, 2) = 3.
C(n, 0) = 1, так как из n элементов выбрать 0 можно единственным образом, а именно, ничего не выбрать.
если k n, то C(n, k) = 0, так как невозможно, например, из трех элементов выбрать пять.
Для вычисления C(n, k) в других случаях используется следующая рекуррентная формула:
C(n, k) = C(n - 1, k) + C(n - 1, k - 1).
По данным числам n и k (0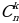 . Для решения используйте рекуррентное соотношение
. Для решения используйте рекуррентное соотношение 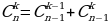 .
.
Решение оформите в виде функции C(n, k).
Входные данные
Вводятся целые числа n и k.
Выходные данные
Выведите ответ на задачу.
Примеры
Входные данные
4
2
Выходные данные
6






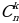 . Для решения используйте рекуррентное соотношение
. Для решения используйте рекуррентное соотношение 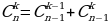 .
.









