Задание 13. ЕГЭ 2022

Задание 13. ЕГЭ 2022

На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E:EA = 5:3, на ребре BB1 - точка F так, что B1F : FB = 5:11, а точка T - середина ребра B1C1. Известно, что AB = 6√2, AD = 10, AA1 = 16.

а) Докажите, что плоскость EFT проходит через вершину D1.

б) Найдите площадь сечения параллелепипеда плоскостью EFT .

Решение.

а) По условию задач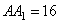и  и 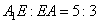, следовательно,  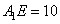и 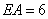. Аналогично для 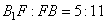, следовательно,  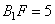и 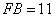. Из полученных значений длин отрезков видно, что подобные треугольник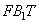и  и 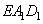 имеют коэффициент подобия 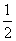, т.е. треугольник  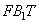имеет длины сторон в 2 раза меньше соответствующих длин треугольника 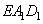. В частности, это означает, что точка T будет проецироваться в точку  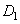при масштабировании плоскости EFT, т.е. плоскость EFT будет проходить через точку .

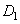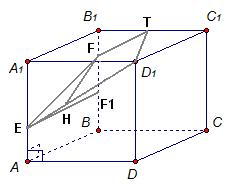
б) Найдем площадь сечения 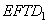. Найдем длину отрезка 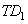. Для этого рассмотрим прямоугольный треугольник 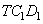, из которого по теореме Пифагора, имеем:

.

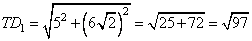Найдем аналогичным образом длину отрезка 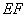 из прямоугольного треугольника  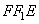(здесь длина ):

.

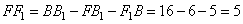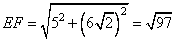Равенство сторон 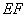 и 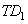 означает, что сечение  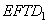является равнобедренной трапецией.

Найдем длину отрезка FT из прямоугольного треугольника :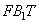

,

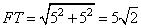длину отрезка 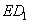 из прямоугольного треугольника :

.

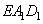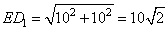Зная основания равнобедренной трапеции, можно найти длину EH по формуле:

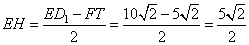
и из прямоугольного треугольника 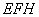 находим высоту трапеции :

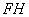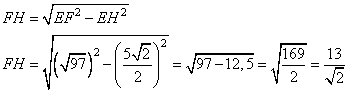
Таким образом, площадь сечения, равна:

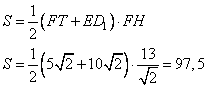
Ответ: 97,5.

Задание 13

На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA =3 : 1, на ребре BB1 - точка F так, что B1F : FB = 1 : 3, а на ребре B1C1 - точка T так, что B1T : TC1 = 1 : 2. Известно, что AB=4, AD=3, AA1=4. a) Докажите, что плоскость EFT проходит через точку D1. б) Найдите угол между плоскостями EFT и BB1C1
Ответ: arccos(1/3)

Задание 13 вариант 38 из 50 вариантов ЕГЭ 2022 Ященко

На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA =2 : 1, на ребре BB1 - точка F так, что B1F : FB = 1 : 5, а на ребре B1C1 - точка T так, что B1T : TC1 = 1 : 3. Известно, что AB=5, AD=4, AA1=6. a) Докажите, что плоскость EFT проходит через точку D1. б) Найдите угол между плоскостями EFT и BB1C1
Ответ: arccos( )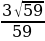

Задание 13 вариант 39 из 50 вариантов ЕГЭ 2022 Ященко

На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA =4 : 3, на ребре BB1 - точка F так, что B1F : FB = 2 : 5, а на ребре B1C1 - точка T так, что B1T : TC1 = 1 : 1. Известно, что AB=3, AD=4, AA1=7. a) Докажите, что плоскость EFT проходит через точку D1. б) Найдите угол между плоскостями EFT и BB1C1
Ответ: arccos(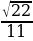 )
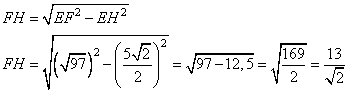
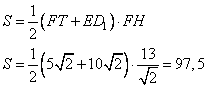
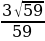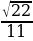