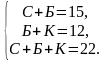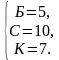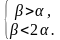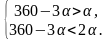Задание № 20. Задачи на логику и смекалку
Тип № 21 (про вазы)
На прилавке цветочного магазина стоят 3 вазы с розами: белая, синяя и красная. Слева от красной вазы 15 роз, справа от синей вазы 12 роз. Всего в вазах 22 розы. Сколько роз в белой вазе?
Решение.
Выясним относительное расположение ваз с розами. Будем обозначать положение вазы соответствующей буквой. Если вазы расположены в порядке Б−С−К, то получится, что в белой и синей вазах в сумме 15 роз, в красной 12 роз, то есть в сумме 27 роз, что противоречит условию задачи. Если вазы располагаются в порядке Б−К−С получаем аналогичное противоречие. Порядок К−Б−С невозможен, потому что тогда справа от синей вазы и слева от красной вазы нет роз. Непротиворечивое расположение ваз: С−Б−К. Будем также обозначать количество роз в вазе соответствующей буквой. Тогда получим систему уравнений:
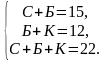
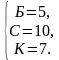
Таким образом, в белой вазе 5 роз.
Ответ: 5.
Задания для самостоятельного решения
1. На прилавке цветочного магазина стоят 3 вазы с розами: оранжевая, белая и синяя. Слева от синей вазы 15 роз, справа от белой вазы 11 роз. Всего в вазах 23 розы. Сколько роз в оранжевой вазе?
2. На прилавке цветочного магазина стоят 3 вазы с розами: белая, жёлтая и оранжевая. Слева от жёлтой вазы 22 розы, справа от оранжевой вазы 23 розы. Всего в вазах 35 роз. Сколько роз в белой вазе?
Тип № 22 (про лучи)
Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 2 раза больше наименьшего. Сколько значений может принимать величина среднего угла?
Решение.
Пусть α − величина наименьшего угла, β − величина среднего угла, тогда 2α − величина наибольшего угла. Полный угол равен 360°, следовательно, α + β + 2α = 360, откуда β = 360 − 3α. Средний угол должен быть больше меньшего угла и меньше большего, то есть:
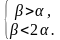
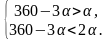
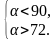
Угол β принимает только значения, измеряемые целым числом градусов, поэтому угол β может принимать 90 − 72 − 1 = 17 значений.
Ответ: 17.
Примечание.
Вычитанием единицы в последнем действии учитывается, что значения 72° и 90° не входят в число значений подсчитываемых углов.
Задания для самостоятельного решения
1. Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 6 раз больше наименьшего. Сколько значений может принимать величина среднего угла?
2. Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 3 раза больше наименьшего. Сколько значений может принимать величина среднего угла?