Россия, Пермь
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 21.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 18.11.2024 17:04
Ненашева Татьяна Васильевна
учитель математики
64 года
7 718
5 986 
Местоположение
Специализация
Задание №21. Подготовка к ОГЭ. Задание №21.
Категория:
Математика
28.01.2023 17:20
Просмотр содержимого документа
«Задание №21. Подготовка к ОГЭ. Задание №21.»
Задание №21
Задача №1
Два велосипедиста одновременно отправляются в 140-километровый пробег. Первый едет со скоростью, на 6 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Задача №1
Два велосипедиста одновременно отправляются в 140-километровый пробег. Первый едет со скоростью, на 6 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Решение:
0 v (км/ч) 1 велосипедист х + 6 2 велосипедист t (ч) s (км) х 140 140 " width="640"
Задача №1
Решение:
Пусть х км/ч − скорость велосипедиста, пришедшего
к финишу вторым, тогда ( х + 6) км/ч − скорость
велосипедиста, пришедшего к финишу первым.
х 0
v (км/ч)
1 велосипедист
х + 6
2 велосипедист
t (ч)
s (км)
х
140
140
Задача №1
Решение:
Задача №1
Решение:
Задача №1
Решение:
Задача №1
Решение:
Задача №1
Решение:
Задача №1
Решение:
Ответ: 14 км/ч.
Задача №2
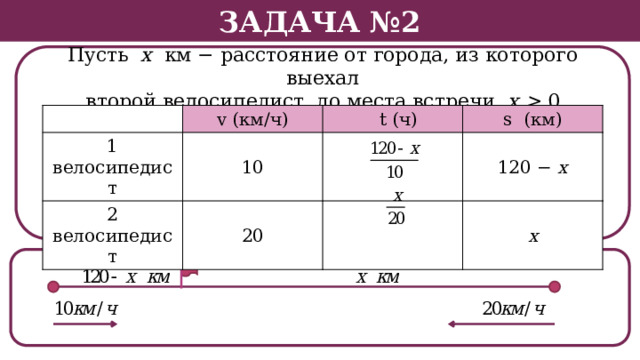
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 120 км, скорость первого велосипедиста равна 10 км/ч, скорость второго − 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Задача №2
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 120 км, скорость первого велосипедиста равна 10 км/ч, скорость второго − 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
0 1 велосипедист v (км/ч) 10 t (ч) 2 велосипедист s (км) 20 120 − х х " width="640"
Задача №2
Пусть х км − расстояние от города, из которого выехал
второй велосипедист, до места встречи. х 0
1 велосипедист
v (км/ч)
10
t (ч)
2 велосипедист
s (км)
20
120 − х
х
Задача №2
Решение:
Задача №2
Решение:
Ответ: 84 км.
Задача №3
Свежие фрукты содержат 88% воды, а высушенные—30%.
Сколько сухих фруктов получится из 35 кг свежих фруктов?
Задача №3
Свежие фрукты содержат 88% воды, а высушенные—30%.
Сколько сухих фруктов получится из 35 кг свежих фруктов?
Решение:
Пусть х кг получится сухих фруктов из 35 кг свежих фруктов.
Вода
Свежие
88%
Сухое вещество
Высушенные
30%
Масса
12%
70%
35 кг
х кг
Задача №3
Свежие фрукты содержат 88% воды, а высушенные—30%.
Сколько сухих фруктов получится из 35 кг свежих фруктов?
Решение:
Ответ: 6 кг.
Задача №4
Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации. Если их смешать, то получится раствор, содержащий 33% кислоты. Если же смешать равные массы этих растворов, то полученный раствор будет содержать 47% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Задача №4
Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации. Если их смешать, то получится раствор, содержащий 33% кислоты. Если же смешать равные массы этих растворов, то полученный раствор будет содержать 47% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Решение:
Пусть х % − концентрация кислоты в первом сосуде,
у % − концентрация кислоты во втором сосуде.
Задача №4
Решение:
Задача №4
Решение:
Задача №4
Решение:
Задача №4
Решение:
Задача №4
Решение:
Задача №4
Решение:
− концентрация кислоты
в первом сосуде
Задача №4
Решение:
− концентрация кислоты
в первом сосуде
(кг) − кислоты
в первом сосуде
Ответ: 2 кг.
Задача №5
Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает
мимо пешехода, идущего параллельно путям со скоростью 4 км/ч
навстречу поезду, за 90 секунд. Найдите длину поезда в метрах .
Задача №5
Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает
мимо пешехода, идущего параллельно путям со скоростью 4 км/ч
навстречу поезду, за 90 секунд. Найдите длину поезда в метрах .
Решение:
1) 26 + 4 = 30( км/ч ) – скорость сближения
Задача №5
Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает
мимо пешехода, идущего параллельно путям со скоростью 4 км/ч
навстречу поезду, за 90 секунд. Найдите длину поезда в метрах .
Решение:
1) 26 + 4 = 30( км/ч ) – скорость сближения
Задача №5
Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает
мимо пешехода, идущего параллельно путям со скоростью 4 км/ч
навстречу поезду, за 90 секунд. Найдите длину поезда в метрах .
Решение:
1) 26 + 4 = 30( км/ч ) – скорость сближения
Задача №5
Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает
мимо пешехода, идущего параллельно путям со скоростью 4 км/ч
навстречу поезду, за 90 секунд. Найдите длину поезда в метрах .
Решение:
1) 26 + 4 = 30( км/ч ) – скорость сближения
Ответ: 750 м.
© 2023, Ненашева Татьяна Васильевна 3176 422
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
