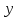ЗАДАНИЕ 23 ОГЭ.
ФУНКЦИИ И ИХ СВОЙСТВА. ГРАФИКИ ФУНКЦИЙ.
ГИПЕРБОЛЫ
(153) Постройте график функции 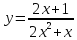 и определите, при каких значениях
и определите, при каких значениях 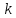 прямая
прямая 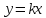 имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Решение.
Найдём область определения данной функции.
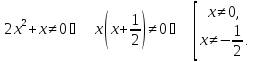
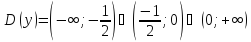 .
.
Упростим выражение, задающее функцию: 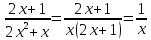 . Значит, исходная функция принимает вид:
. Значит, исходная функция принимает вид:
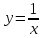 – обратная пропорциональность, графиком является гипербола, ветви которой симметричны относительно начала координат и расположены в I и III четверти, т.к.
– обратная пропорциональность, графиком является гипербола, ветви которой симметричны относительно начала координат и расположены в I и III четверти, т.к. 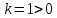 .
.
Поскольку , то выколотая точка имеет координаты
, то выколотая точка имеет координаты  .
.
Для того, чтобы прямая 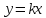 имела с этой гиперболой только одну общую точку, необходимо, чтобы она прошла именно через выколотую точку, т.е.
имела с этой гиперболой только одну общую точку, необходимо, чтобы она прошла именно через выколотую точку, т.е.  и прямая задана формулой
и прямая задана формулой  .
.
Ответ: 
(314796) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях 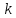 прямая
прямая 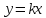 имеет с графиком одну общую точку.
имеет с графиком одну общую точку.
Решение.
Найдём область определения данной функции.
.
Упростим выражение, задающее функцию:  . Значит, исходная функция принимает вид:
. Значит, исходная функция принимает вид:
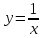 – обратная пропорциональность, графиком является гипербола, ветви которой симметричны относительно начала координат и расположены в I и III четверти, т.к.
– обратная пропорциональность, графиком является гипербола, ветви которой симметричны относительно начала координат и расположены в I и III четверти, т.к. 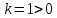 .
.
Поскольку , то выколотая точка имеет координаты
, то выколотая точка имеет координаты  .
.
Для того, чтобы прямая 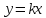 имела с этой гиперболой только одну общую точку, необходимо, чтобы она прошла именно через выколотую точку, т.е.
имела с этой гиперболой только одну общую точку, необходимо, чтобы она прошла именно через выколотую точку, т.е.  и прямая задана формулой
и прямая задана формулой  .
.
Ответ: 
(314804) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях 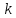 прямая
прямая 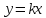 имеет с графиком одну общую точку.
имеет с графиком одну общую точку.
Решение.
Найдём область определения данной функции.
.
Упростим выражение, задающее функцию:  . Значит, исходная функция принимает вид:
. Значит, исходная функция принимает вид:
 – обратная пропорциональность, графиком является гипербола, ветви которой симметричны относительно начала координат и расположены во II и IV четверти, т.к.
– обратная пропорциональность, графиком является гипербола, ветви которой симметричны относительно начала координат и расположены во II и IV четверти, т.к.  .
.
Поскольку , то выколотая точка имеет координаты
, то выколотая точка имеет координаты  .
.
Для того, чтобы прямая 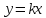 имела с этой гиперболой только одну общую точку, необходимо, чтобы она прошла именно через выколотую точку, т.е.
имела с этой гиперболой только одну общую точку, необходимо, чтобы она прошла именно через выколотую точку, т.е.  и прямая задана формулой
и прямая задана формулой  .
.
Ответ: 
(340933) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  не имеет с графиком ни одной общей точки.
не имеет с графиком ни одной общей точки.
Решение.
Найдём область определения данной функции. Т.к. знаменатель не может равняться нулю, то . Значит,
.
Упростим выражение, задающее функцию.
Итак, исходная функция, после упрощения, имеет вид:
 – обратная пропорциональность, графиком является гипербола, которая получается из графика функции
– обратная пропорциональность, графиком является гипербола, которая получается из графика функции  смещением вдоль оси Оу на 3 ед. отрезка вверх.
смещением вдоль оси Оу на 3 ед. отрезка вверх.

Поскольку , то выколотая точка имеет координаты
, то выколотая точка имеет координаты  .
.
Для того, чтобы прямая  не имела с этой гиперболой ни одной общей точки, необходимо, чтобы она прошла именно через выколотую точку, или через точку
не имела с этой гиперболой ни одной общей точки, необходимо, чтобы она прошла именно через выколотую точку, или через точку  т.е.
т.е.  .
.
Ответ:  .
.
ЗАДАЧИ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
(314799) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях 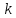 прямая
прямая 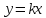 имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
(338224) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  не имеет с графиком ни одной общей точки.
не имеет с графиком ни одной общей точки.
(341420) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  не имеет с графиком ни одной общей точки.
не имеет с графиком ни одной общей точки.
(357524) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  не имеет с графиком ни одной общей точки.
не имеет с графиком ни одной общей точки.
(357525) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  не имеет с графиком ни одной общей точки.
не имеет с графиком ни одной общей точки.
(357526) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  не имеет с графиком ни одной общей точки.
не имеет с графиком ни одной общей точки.
(357527) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  не имеет с графиком ни одной общей точки.
не имеет с графиком ни одной общей точки.
(357528) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  не имеет с графиком ни одной общей точки.
не имеет с графиком ни одной общей точки.
(357529) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  не имеет с графиком ни одной общей точки.
не имеет с графиком ни одной общей точки.
(357532) Постройте график функции  и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  не имеет с графиком ни одной общей точки.
не имеет с графиком ни одной общей точки.
ОТВЕТЫ
| № задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ответ | 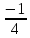
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
3







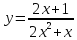 и определите, при каких значениях
и определите, при каких значениях 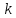 прямая
прямая 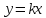 имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.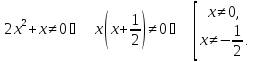
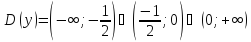 .
.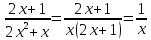 . Значит, исходная функция принимает вид:
. Значит, исходная функция принимает вид: 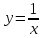 – обратная пропорциональность, графиком является гипербола, ветви которой симметричны относительно начала координат и расположены в I и III четверти, т.к.
– обратная пропорциональность, графиком является гипербола, ветви которой симметричны относительно начала координат и расположены в I и III четверти, т.к. 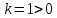 .
.